§23. Флуктуации физических величин.

Пусть есть - физическая величина, которая при измерении с вероятностьюдает величину, тогда мы можем говорить о среднеми о дисперсии, где

.

Мы вводили флуктуацию

,

отклонение величины от ее среднего значения.

Перенесем все это на язык квантовой механики, т. к. физической величине мы ставим в соответствие.

Можно показать, что .

Неравенство Коши-Шварца: Оно справедливо и для функциональных пространств, в том числе и для Гильбертова пространства, которое рассматривается в квантовой механике.

Для двух векторов оно имеет вид

имеет смысл тот, что .

, .

Теперь если обозначить ,, тогда будем также рассматривать статистическое усреднение. Отсюда получим из неравенства Коши-Шварца:

Теперь если определить . К тому же по определению изимеем, тогда. Из этого следует, что

.

В случае квантовой механики заменяем на , тогда

.

§ 24. Неравенство Гайзенберга.

Канонически сопряженные величины одновременно неизмеримы – это принцип неопределенности.

Под канонически сопряженными понимаем величины и.

В квантовой механике для операторов и, которые поставлены в соответствие канонически сопряженным величинам имеем

.

Более того , а сам коммутаторимеет вид оператора.

Это можно записать в виде .

Если , то, тогда, где.

, т.к. и есть числа.

Обозначим . Здесь- единичный оператор.

Тогда из получим(*)

Введем обозначение

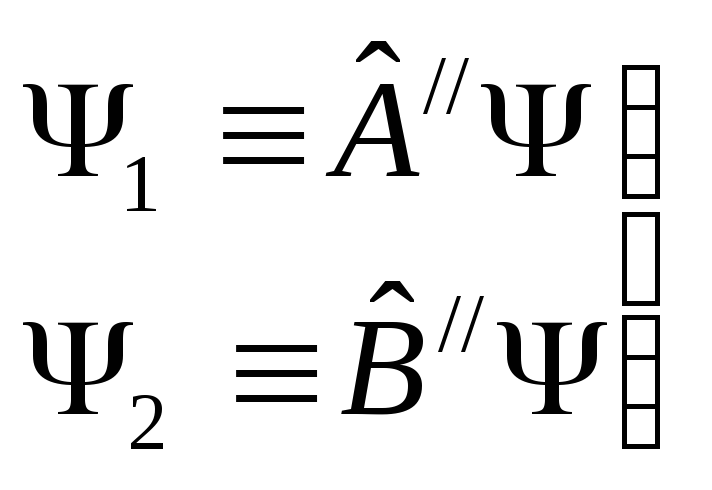
Подставим это в неравенство Коши-Шварца, тогда

Используем эрмитовость операторов

,

,

тогда

.

Поделим левую и правую части на , тогда

Используем определение среднего

,

тогда

.

Или

Операторы ине коммутируют, тогда

.

Первое слагаемое обозначим ,.

Второе слагаемое .

Оператор дает чисто вещественное число, адает чисто мнимое число.

Тогда

,

где .

.

Окончательно

.

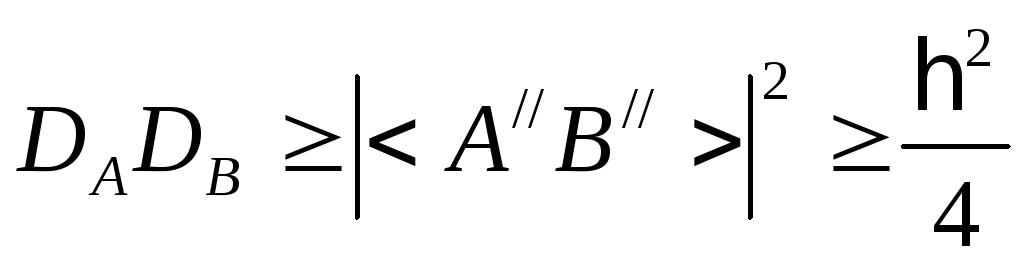В полученном неравенстве математически заложен принцип неопределенности Гайзенберга.

Если величина измерена точно, то ,т.е..

Если , то величинаA измерена точно и , но тогда для, т. к.. Из этого следует, что канонически сопряженная величинаB не измерима.

Когда измеряем величину , то получаем спектр значений, которые выходят с вероятностью. Для того чтобынеобходимо чтобы система находилась в состоянии.

§ 25 Оператор Гамильтона различных систем.

Этот вопрос идентичен рассмотренной в классической механике будут те же соотношения, но для операторов

.

Поставим в соответствие конкретной системе операторы и:

В декартовой системе координат ,.

Здесь n – число точек в системе.

.

- функция от оператора координаты.

Мы рассматриваем - представление, здесь

Мы рассматриваем декартову систему координат. Гамильтониан мы поставили в соответствие системе материальных точек. Эта система незамкнутая, т. к. потенциальная энергия зависит от времени. (т. е. здесь нет однородности времени).

Перейдем к более простой задаче. Рассмотрим систему N материальных точек во внешнем стационарном поле

Здесь отвечает за внутреннее взаимодействие между частицами.

отвечает за внешнее воздействие на систему частиц.

.

Выражение, описывающее внешнее воздействие обладает аддитивностью, т. е.

.

Индекс a означает, что разные частицы могут взаимодействовать с внешним полем по разному закону. Если все частицы одинаковые и одинаково взаимодействуют с внешним полем, то индекс a убирается.

Внутреннее взаимодействие неаддитивно.

Рассмотрим случай свободной материальной точки. Соответственно она ни с чем не взаимодействует:

Тогда , или в-представлении, то

,

тогда .

Если материальная точка во внешнем поле:

, ,

Нестационарное поле .

Стационарное поле .

Центральное поле .

Рассмотрим систему двух материальных точек. Мы рассматриваем частный случай – замкнутая система двух материальных точек.

В случае классической механики: .

Отсутствие t в энергии взаимодействия – это однородность времени и закон сохранения энергии.

Зависимость энергии от модуля есть изотропность пространства.

В квантовой механике в -представлении:

,

,

где