- •Квантовая механика
- •§ 1. Экспериментальные основы квантовой механики
- •§ 2. Классическое и квантовое описание системы.
- •§ 3 Принцип неопределенности.
- •§ 4. Полный набор динамических переменных
- •§ 5. Постулаты квантовой механики.
- •§ 6 Роль классической механики в квантовой механике
- •§ 7 Волновая функция и ее свойства.
- •§ 8 Принцип суперпозиции состояний
- •§ 9 Понятие о теории представлений
- •§ 10 Операторы в квантовой механике
- •§ 12 Среднее значение измеряемой величины.
- •§ 13 Вероятность результатов измерения
- •§ 14 Коммутативность операторов и одновременная измеримость физических величин
- •§ 15. Операторы координаты , импульса, момента импульса, энергии.
- •§ 16. Решение задачи Штурма-Лиувилля для оператора .
- •§ 17 Решение задачи Штурма-Лиувилля для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы .
- •§ 19 Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в кв. Механике.
- •§ 22. Свойства операторов вида
- •§23. Флуктуации физических величин.
- •§ 24. Неравенство Гайзенберга.
- •§ 25 Оператор Гамильтона различных систем.
- •§ 26. Стационарное состояние различных систем
- •§ 27. Решение волнового уравнения в случае свободной материальной точки
- •Для трехмерного случая
- •§ 28. Интегральные операторы в квантовой механике.
- •§ 29. Интегральный оператор канонического преобразования.
- •§ 30. Каноническое преобразование оператора.
- •§ 31. Уравнения Шредингера в матричной форме.
- •§ 32. Линейный гармонический осциллятор
- •Предельные технологические размеры кристаллов и.С. 0.1 – 0.5 мкм. Существует и предел по физической работоспособности. Однако с уменьшением размера кристалла увеличивается быстродействие приборов.
- •§ 30.1. Каноническое преобразование оператора. Ч. 2
- •§ 34. Унитарные инварианты в квантовой механике.
- •§ 35. Вид операторов ив декартовых и сферических координатах.
- •§ 36. Коммутационные соотношения с оператором .
- •§ 37. Собственные функции и собственные значения операторов и.
- •§ 38. Вырождение энергетических уровней частицы, движущейся в центральном поле.
- •§ 39. Гамильтониан частицы без спина, движущейся в магнитном поле.
- •§ 40. Снятие вырождения по квантовому числу m в случае частицы без спина, движущейся в магнитном поле. Используем
- •§ 41. Оператор бесконечно малого поворота без учета спина.
- •§ 42. Собственный механический момент (спин).
- •§ 43. Операторы ии их свойства.
- •§ 44. Спиновая переменная волновой функции
- •§ 45. Матрицы Паули и их свойства.
- •§ 46 Понятие о спинорах
- •§ 47. Уравнение Паули Мы писали волновое уравнение в виде
- •§ 48. Операторы и, и их свойства
- •§ 50. Принцип тождественности.
- •§ 51. Оператор перестановки и его свойства
- •§ 52. Симметричное и антисимметричное состояния.
- •§ 53. Обменное взаимодействие
- •§ 54. Основное состояние атома гелия
- •§ 55. Схема Юнга квантовой механики.
- •1. И ,
- •2. И .
- •§ 56. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения.
- •§ 58 Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближения.
- •§ 59. Критерий применимости теории возмущений.
- •§ 60. Стационарная теория возмущений в случае близких энергетических уровней.
- •§ 61. Метод (представление) Шредингера. Оператор эволюции и его свойства.
- •§ 62. Метод (представление) Гейзенберга. Уравнение движения для оператора.
- •§ 63. Уравнение эволюции среднего значения физической величины. Соотношение неопределенности: время – энергия.
- •§ 64. Матричное представление операторов.
- •§ 65. E – представление.
- •§ 66. Уравнение Шредингера в матричной форме.
- •§ 67. Матричная формулировка задачи о линейном гармоническом осцилляторе.
- •§ 68. Расчет матричных элементов операторов .
§ 54. Основное состояние атома гелия
Рассмотрим основное одночастичное состояние:
![]() .
.
Здесь
удобно перейти к атомным (кулононовским)
единицам, чтобы исключить константы
![]() ,
,![]() ,
,![]() ,
тогда
,
тогда
![]() .
.
В кулоновских единицах одночастичная функция для основного состояния выглядит:
![]() .
.
Каким
квантовым числам соответствет
одночастичное состояние? Вводят три
квантовых числа (без спина):
![]() ,
,
![]() ,
,![]() .
Для основного одночастичного состояния
1, 0, 0 соответственно.
.
Для основного одночастичного состояния
1, 0, 0 соответственно.
Тогда, ставим индексы
![]() .
.
Эта функция нормирована на единицу, т. е.
![]() .
.
Если взять симметричные и антисимметричные функции для двух частиц в основном состоянии, то имеем:
![]() ,
,
![]() .
.
И получаем, что основное состояние описывает симметричная функция. Вычисление энергии одночастичного состояния для центрального поля мы проводили и получали в размерных единицах
![]() .
.
Или в кулоновских единицах
![]() .
.
![]() ,
,
![]() .
.
Так как у нас два электрона, то есть две частицы, то
![]() .
.
В первом приближении, энергия основоного состояния для атома Гелия в атомных единицах
![]() .
.
В самосогласованном методе решение оказывается:
![]() .
.
Из эксперимента
![]() .
.
Задача
Определить приближенно энергию основного уровня атома гелия (ядро с зарядом Z и два электрона), рассматривая взаимодействие между электронами как возмущение.
Решение
В основном состоянии иона оба электрона находятся в S-состояниях. Невозмущенное значение энергии равно удвоенному основному уровню водородоподобного иона:
![]() .
.
Поправка первого приближения дается средним значением энергии взаимодействия электронов, взятом по состоянию с волновой фуркцией
![]() .
.
(произведение
двух водородоподобных функций с
![]() )
)
Интеграл
![]()
проще всего вычислить так
 ,
,
![]() ,
,
![]() .
.
Энергия
распределение зарядов
![]() в поле сферически – симметричного
распределения
в поле сферически – симметричного
распределения![]() .
Подынтегральное выражение интеграла
по
.
Подынтегральное выражение интеграла
по![]() есть энергия заряда
есть энергия заряда![]() в поле сферы
в поле сферы![]() .
Множитель 2 перед интегралом учитывает
вклад от конфигураций, в которых
.
Множитель 2 перед интегралом учитывает
вклад от конфигураций, в которых![]() .
Таким образом, получим
.
Таким образом, получим
![]() .
.
Окончательно
![]() .
.
Когда рассчитываем основное состояние, то функция основного состояния должна быть
![]() ,
,
однако, ранее мы получили формулу
![]() .
.
Мы все это рассчитываем через
![]() (*)
(*)
Однако, правильный результат получается из
![]() .
.
Тогда
в формуле (*) стоит при
![]() лишня двойка, которая потом дала
лишня двойка, которая потом дала![]() .
.
§ 55. Схема Юнга квантовой механики.
Мы рассматривали систему двух электронов. Волновая функция системы двух электронов была:
![]() .
.
Т. е. в гамильтониане не учтен спин и мы можем разделить переменные.
Возможно два варианта:
1. И ,
2. И .
Тогда, мы учитавая принцип тождественности, неявно учитывали спин в теории.
Распространим этот принцип на систему с большим числом электронов.
Так
как у электрона два значения спина
![]() ,
то вводится схема Юнга.
,
то вводится схема Юнга.
Обозначения:

По горизонтали проводят симметризацию, а по вертикали антисимметризацию.
Будем обозначать цифрами координаты. Пусть есть 3 частицы, тогда:
![]() .
.
Подействуем операторами перестановки:
![]() . (*)
. (*)
Теперь рассмотрим
![]() , (**)
, (**)
В результате получаем, что разность (*) и (**) не равна нулю
![]() .
.
Это значит, что соответствующие величины одновременно не измеримы, у них нет общего базиса и они не могут быть вместе приведены к диагональному виду. То, что у этих операторов различные базисы, т. е. различные собственные функции и показывает, что симметризация не может быть такой простой, как для двух электронов. Задача симметризации относится уже к теории групп.
Вообще
говоря,
![]() - антисимметричная, т. к. мы рассматриваем
фермионы.
- антисимметричная, т. к. мы рассматриваем
фермионы.
Тогда, имеем:
![]() :
:
![]() соотсетствует
соотсетствует![]()
![]()
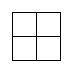
![]() :
:
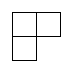 соотсетствует
соотсетствует![]() :
: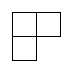
Здесь координаты не ставят, т. к. рассматривают перестановки по всем координатам, а потом выбирают независимые. Т. е. рассматривают просто схемы симметризации.
Суммарному
спину
![]() соответствует рисунок
соответствует рисунок
![]()
![]() и
и
![]() :
:![]() ,
,
а
суммарному спину
![]() соответствует
соответствует
![]() :
:
 соотсетствует
соотсетствует
![]() :
:
При большем числе электронов картина становится следующей:
|
|
|
Спин |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
Мы
можем установить взаимоодназначное
соответствие между картинкой симметрии
и спином
![]() .
Хотя спин в оператор
.
Хотя спин в оператор![]() не входит, мы его вводим через принцип
тождественности.
не входит, мы его вводим через принцип
тождественности.