§ 16. Решение задачи Штурма-Лиувилля для оператора .

Оператор импульса – оператор с непрерывным спектром собственных значений.

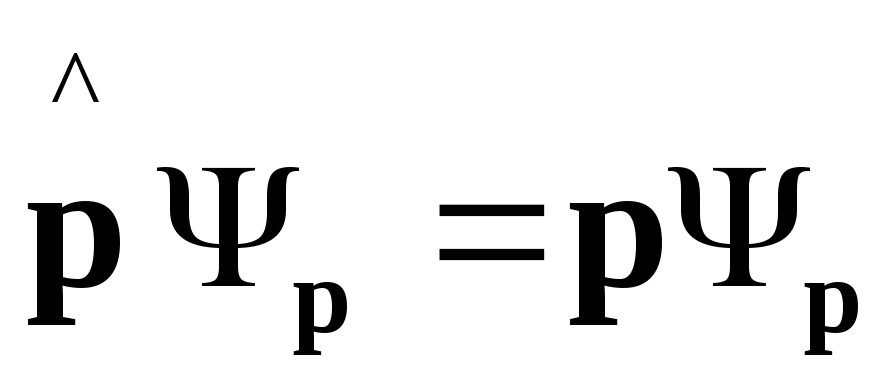(1)

Мы рассматриваем координатное представление, тогда - функция координат.

Оператор векторный, он имеет трикомпоненты:

Например:

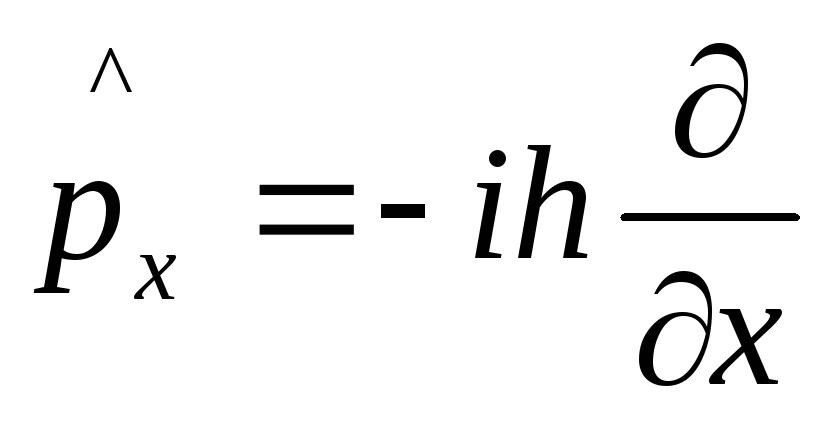(2)

Тогда уравнение (1) разваливается на три независимых члена, т.к. операторы коммутируют.

Существует утверждение, что если можно представить в виде суммы коммутирующих операторов:

, ,

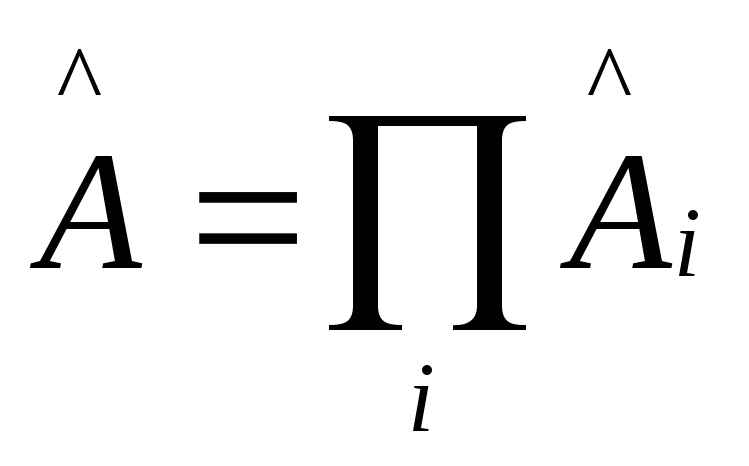то задача Штурма-Лиувилля 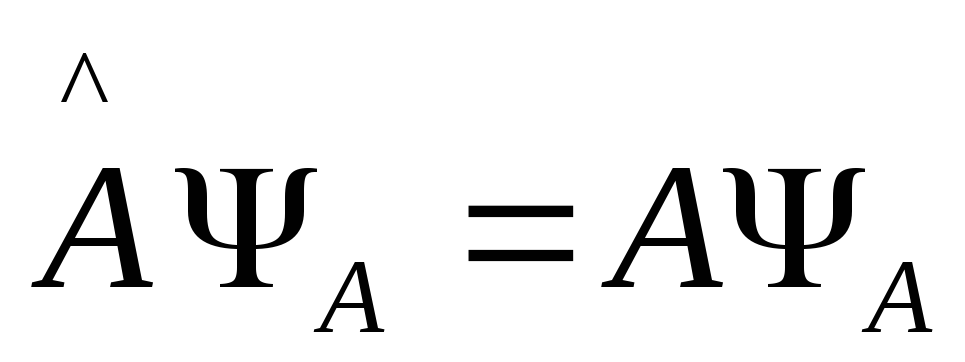распадается на подзадачи этих коммутаторов:

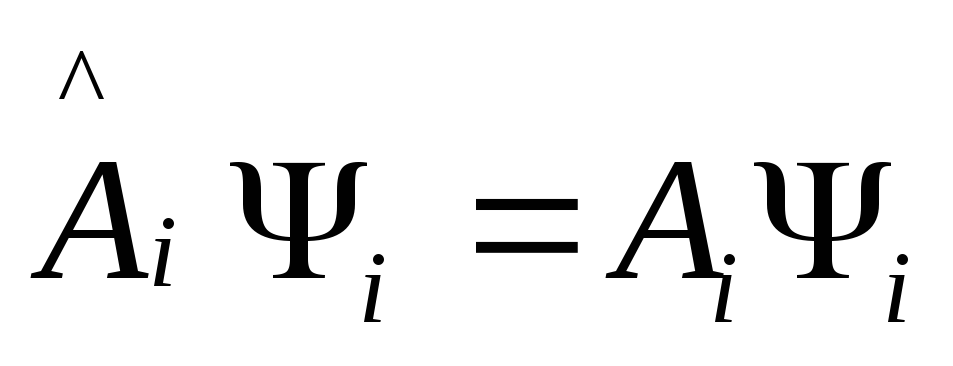
Для задачи (1) имеем:

,

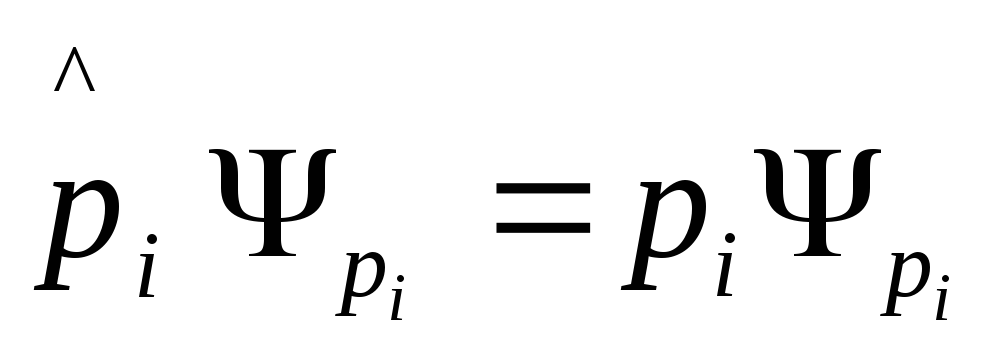где i принимает значения 1,2,3

Решим случай i=1, тогда

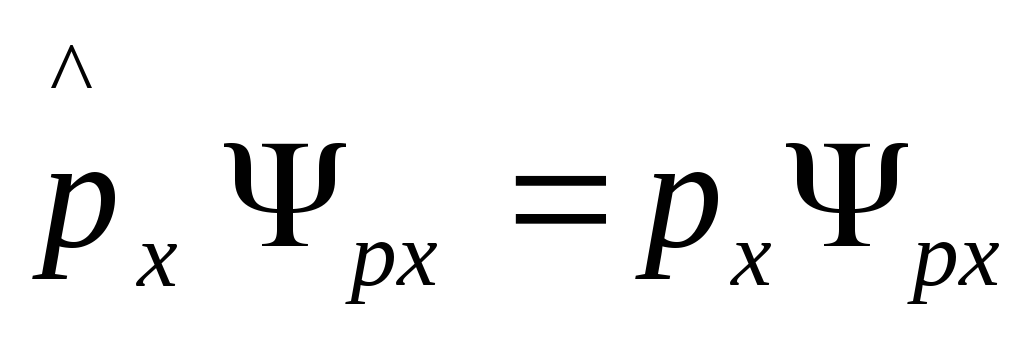(3)

Подставляем (2) в (3) и временно опустим индекс px у , тогдаимеем

т.к. - функция одной переменной,тогда

здесь - число, собственное значение.

Запишем тоже с индексами:

При решении задачи получили, что p имеет непрерывный спектр на всей числовой оси. Т. е. - не квантуется.

Найдем . Используем условие ортонормированности.

В нашем случае:

,

Тогда:

(4)

.

.

Обозначим .

.

Тогда

Интеграл дает с точностью до множителя - функцию, поскольку:

Используем следующее свойство -функции:

.

В нашем случае получим

,

тогда

(5)

Подставляем (5) в (4)

В связи с тем, что волновые функции в квантовой механике определены с точностью до фазового множителя, то

.

Фаза точно не определена, и ее можно отнести к самой волновой функции. Такая неоднозначность принципиальна и не может быть устранена, однако она несущественна, так как не отражается ни на каких физических величинах. Таким обрахзом: .

Мы получили

Теперь запишем

(6)

Функция (6) удовлетворяет условию нормировки (4).

В импульсном представлении:

§ 17 Решение задачи Штурма-Лиувилля для оператора .

Если в классической механике рассматривать , то

.

Если полученному выражению поставить в соответствие оператор в квантовой механике, то он может быть записан в ви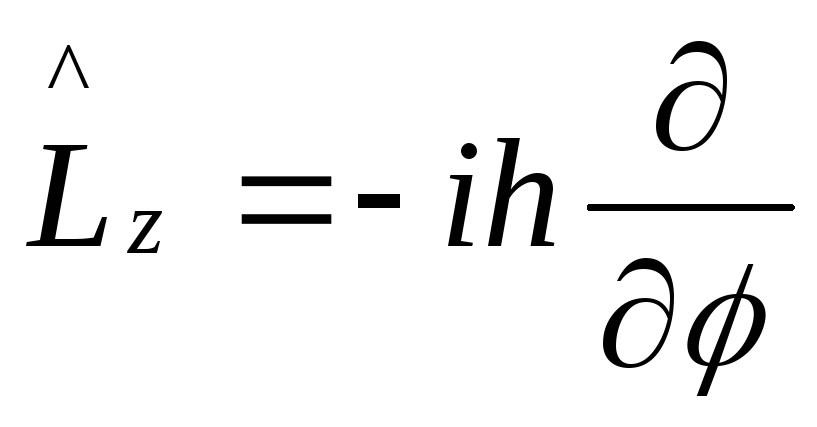де:

, где - угол поворота вокруг оси.

Задача Штурма-Лиувилля для оператора :

,

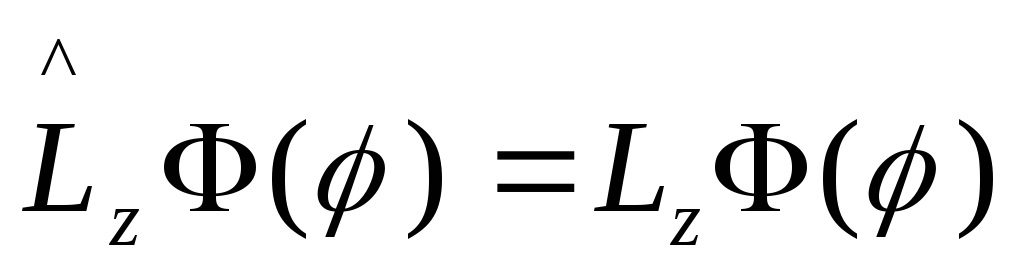
где .

Решение для :.

Мы накладываем на функцию условие периодичности, т. к. уголменяется отдо, т. е..

Это ограничение приводит к виду собственной функции:

Поскольку если , то, то получаем, что , гдеN и M целые числа. Отсюда должно быть целым. Приравниваем . Отсюда получаемдля .- целое безразмерное число.

Из условия периодичности получили квантованность проекции орбитального момента на ось z. Спектр собственных значений оператора дискретный.

Так как целое число, то функция приобретает индекс.

Найдем константу :

Условие нормировки .

{при интеграл дает 0, только при интеграл не равен 0}

При интеграл дает

Тогда имеем для уравнения 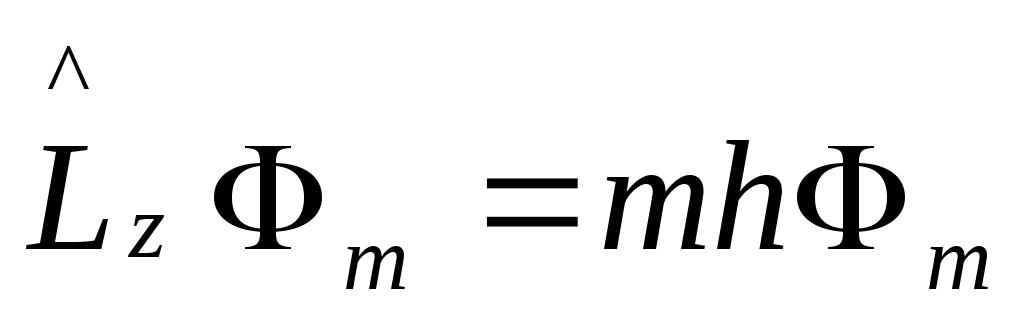собственную волновую функцию

Здесь получили дискретный спектр собственных значений и нормируемость собственной функции.

§ 18. Вычисление коммутаторов, содержащих операторы .

Для оператора :

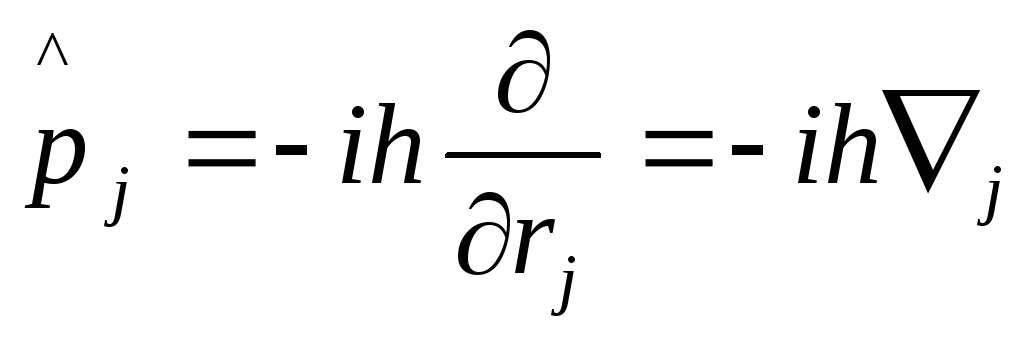
Найдем , где- есть функцияи, т.е.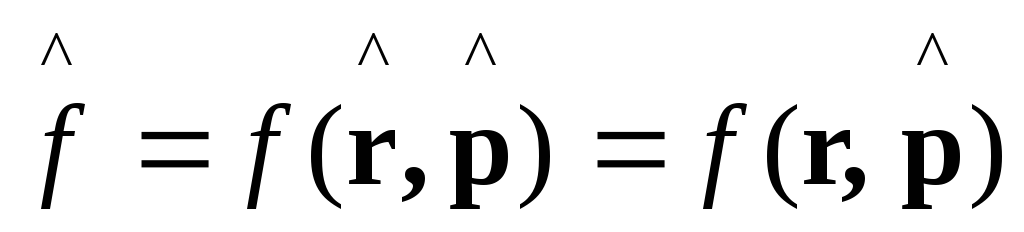- координатное представление.

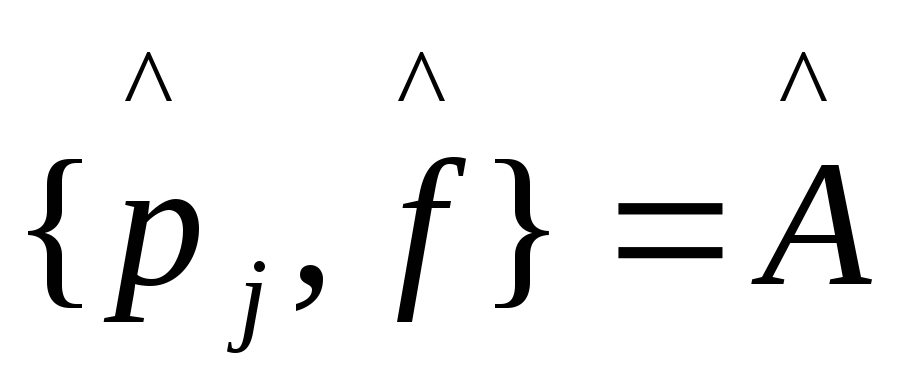
Это равенство понимается в том смысле, что при действии коммутатора на любую функцию, равенство выполняется.

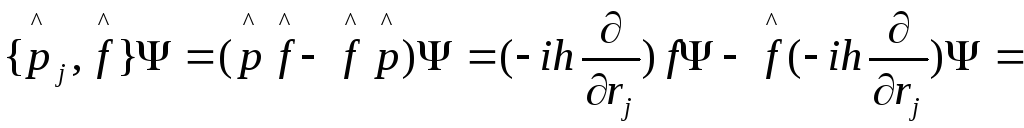{распишем это},

теперь

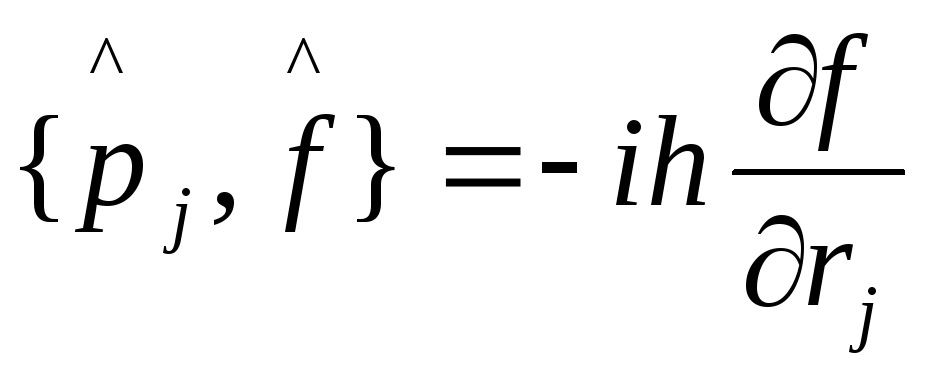, (1)

т.к. - произвольная функция.

Аналогичный результат для оператора :

,

в импульсном представлении.

, (2)

здесь .

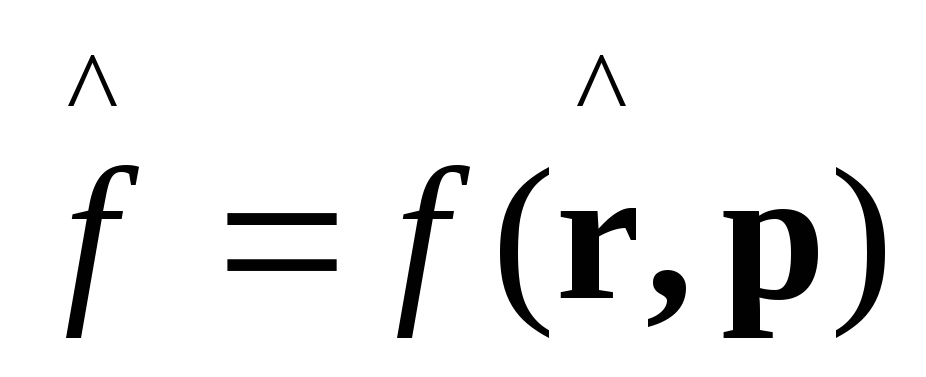Рассмотрим частные случаи формул (1) и (2):

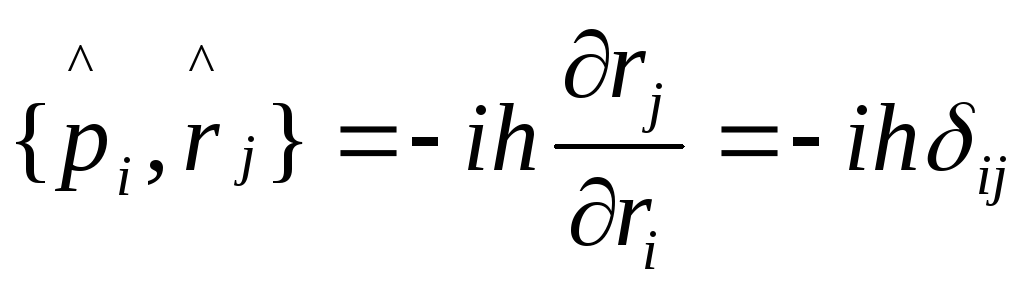1. , здесь играет роль функции.

2. 

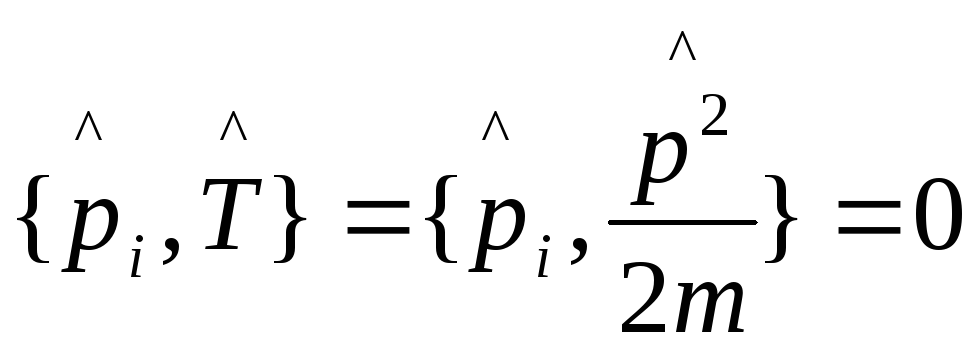
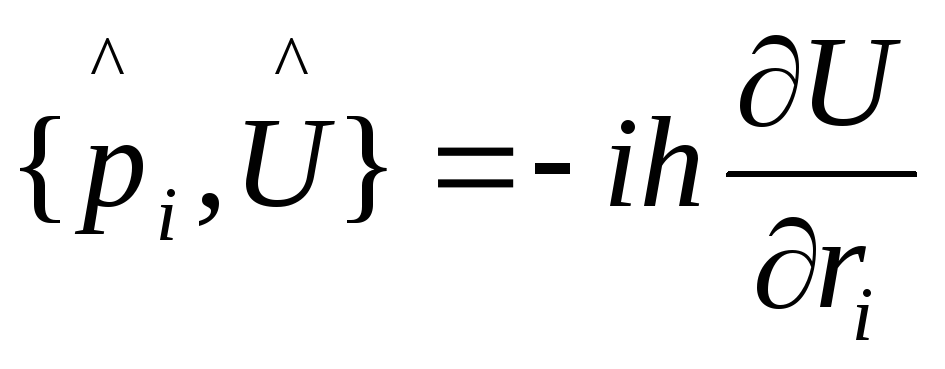3. , здесь 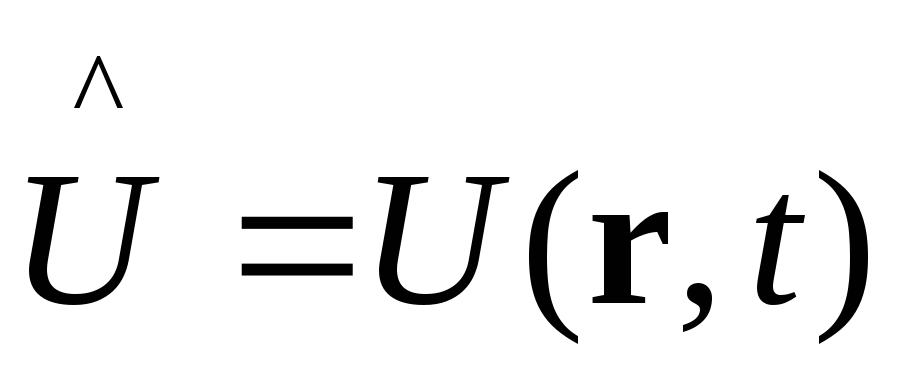потенциальная энергия - функция координат и времени.

3a.

4. 

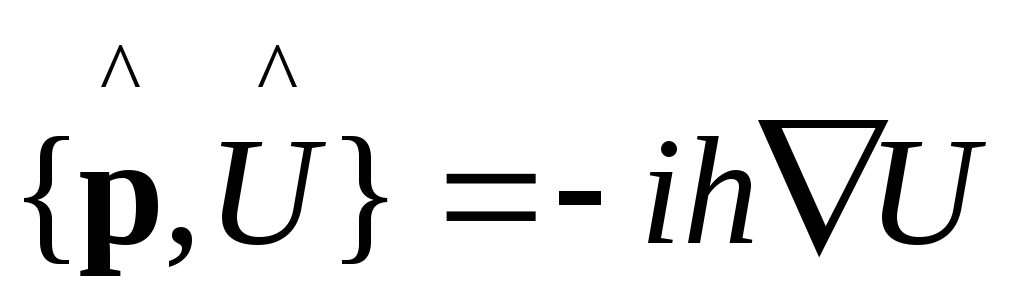
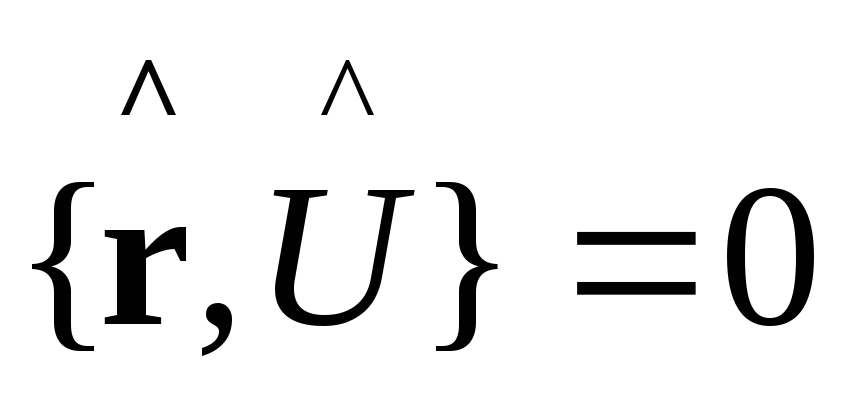
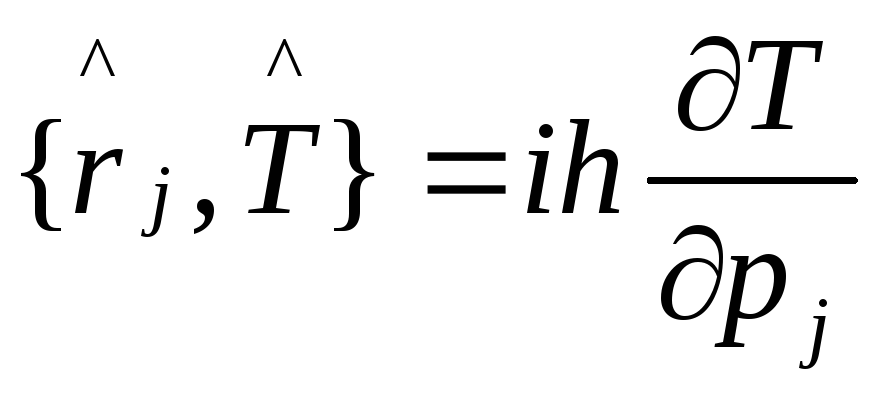5. , здесь импульсное представление, таким образом .

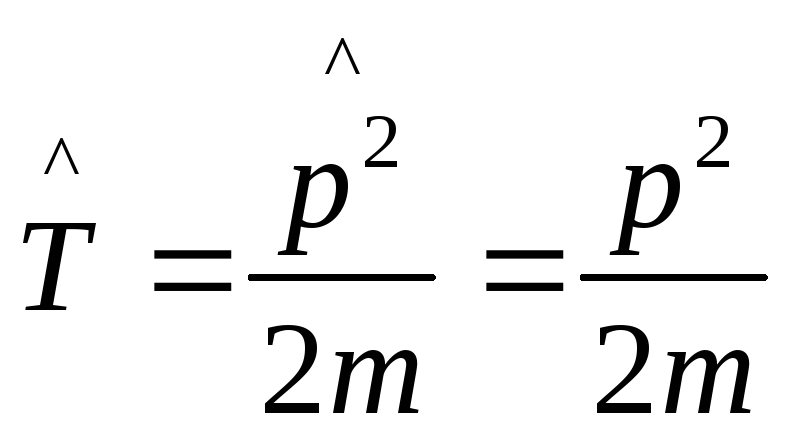5a. 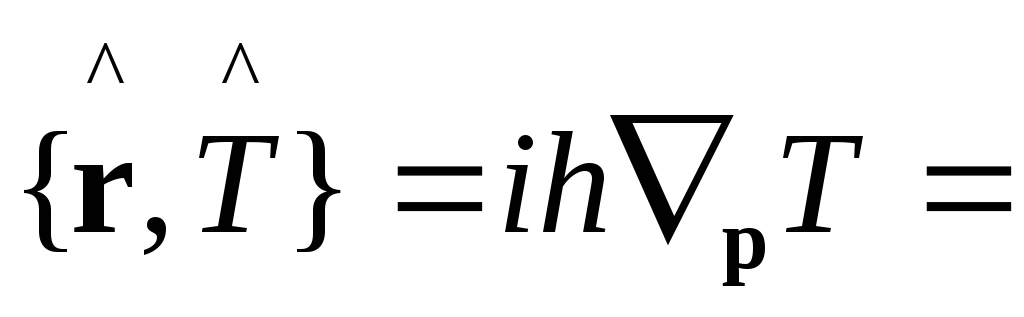{для одной материальной точки }-это справедливо и в координатном и в импульсном представлении. Для координатного , а для импульсного.

6. -координатное представление.

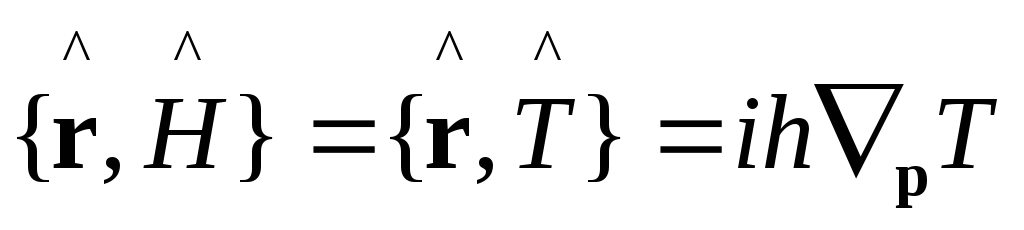7. -импульсное представление

Рассмотрим соотношение для оператора

Используем дополнительное соотношение:

{используем (1) и (2): 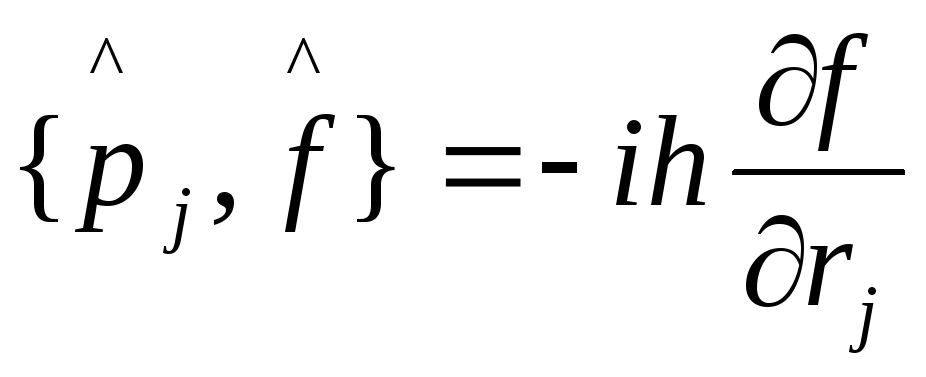,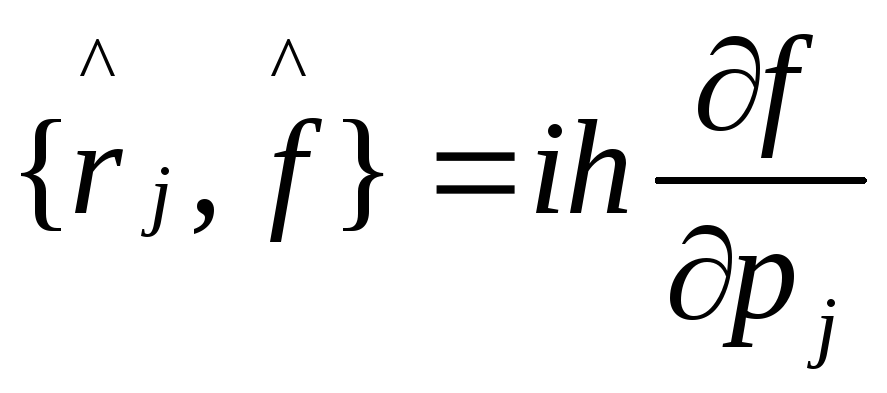}{, тогда второе слагаемое } ={в классической математике измерение компонента вектора при бесконечно малом повороте:

,

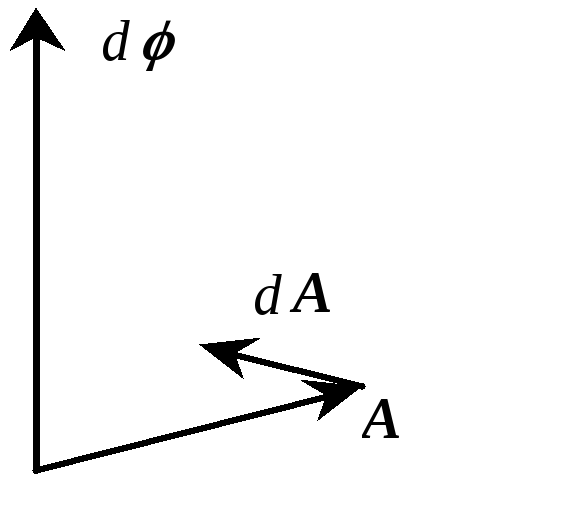
это оотношение справедливо и в квантовой теории поля:

}={}={,

. В общем случае импульс и координата не коммутируют, тогда функция координат и импульсов и импульс, координата и функция координат и импульсов не коммутируют. Если f – функция скалярная, тогда она не меняется при вращении. В этом случае, чтобы , тоf – векторная функция.} (где f есть компонента некоторой векторной величины, т. е. .

Тогда перепишем в виде :

{меняем местами индексы}

Тогда для любой векторной функции имеем:

Здесь вместо можно подставить, например,

- коммутатор с любым скаляром равен нулю.

Получим: