§ 36. Коммутационные соотношения с оператором .

Раньше было получено:

(*)

и также

(**)

, (***)

где - скалярный оператор.

Рассмотрим оператор .

Найдем коммутатор

или

из этого имеем

Найдем произведение

Анаогично

Теперь для

(4*)

§ 37. Собственные функции и собственные значения операторов и.

Для соотношения были получены ранее:

Т. к. операторы и- коммутируют

они обладают общим базисом.

Было показано, что

,

тогда его собственная функция удовлетворяет уравнению

Произведем разделение переменных

В этом случае, запишем

Здесь можно рассматривать как множитель, т. к. оператор на нее не действует.

Ранее было показано

Усредним

Здесь мы имеем равенство только тогда, когда m=0 и .

Таким образом получаем ограничение на среднее

и одновременно измеримы, т. к. они коммутируют. Это значит, что они одновременно измеримы и обладают общим базисом собственных функций. Тогда

.

Отсюда

,

Рассмотрим теперь соотношение

Подействуем этим оператором на функцию

для максимального , т. е.

.

Тогда

Так как - есть собственная функция оператора, то имеем

.

Обозначив

имеем

Это задача Штурма-Лиувилля для оператора . Максимальное собственное значение дляесть, но у нас. Таким образом.

Подействуем оператором

Тогда

Теперь

- орбитальное число.

Теперь

.

Выясняется, что

.

Здесь - полином Лежандра.

Условие нормировки для записанных шаровых функций

Рассмотрим величину орбитального момента:

Тогда

При переходе к классической механике: . Определим величину предела .

В классической механике существует величина момента импульса, тогда при мы не должны получать 0. Учтем произвол . Таким образом возникает. При этом

§ 38. Вырождение энергетических уровней частицы, движущейся в центральном поле.

Центральное поле – это поле которое зависит только от , т. е. оно обладает сферической симметрией. Рассмотрим частный случай центрального поля – кулоновский потенциал. Задача для 1 частицы – 3 степени свободы.

Будем решать задачу в -представлении и в стационарном поле.

Размерность

Для взаимодействия двух различных по величине зарядов имеем

В атоме водорода:

,

где e –заряд электрона.

Выясняется, что состояние системы, в силу стационарности задачи

найдем из стационарного уравнения Шредингера

(*)

Гамильтониан системы

Так как имеем сферическую симметрию, то удобно использовать сферические координаты:

Разделяем угловую и радиальную части

.

При решении (*) у нас появятся квантовые числа

n – главное квантовое число.

При этом

Тогда

l=0,…,n-1

Возникла ситуация, когда энергетическому уровню соответствует несколько квантовых состояний с разичными значениямиl и m – т. е. возникла ситуация вырождения энергетического уровня.

Число квантовых состояний, отвечающих данному жнергетическому уровню называется кратностью вырождения.

При фиксированном l:

,

т. е. значениеl.

Кратность вырождения энергетического уровня с главным квантовым числом равна

С учетом спина, кратность вырождения .

§ 39. Гамильтониан частицы без спина, движущейся в магнитном поле.

При разборе аналогичной задачи в классической механике функция имела вид

Если поле электромагнитное, то , где- скалярный потенциал электромагнитного поля.

Если поле магнитное, то .

Величина

импульс в магнитном поле. -обобщенный импульс частицы.

Мы рассматриваем магнитное поле, тогда ъ

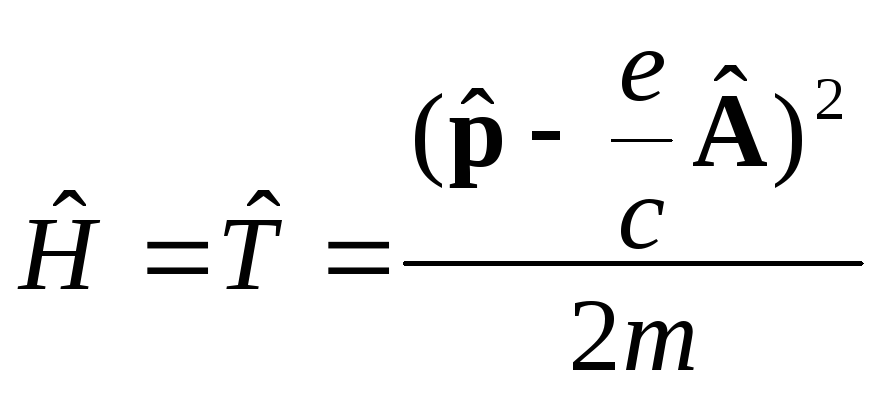
Распишем

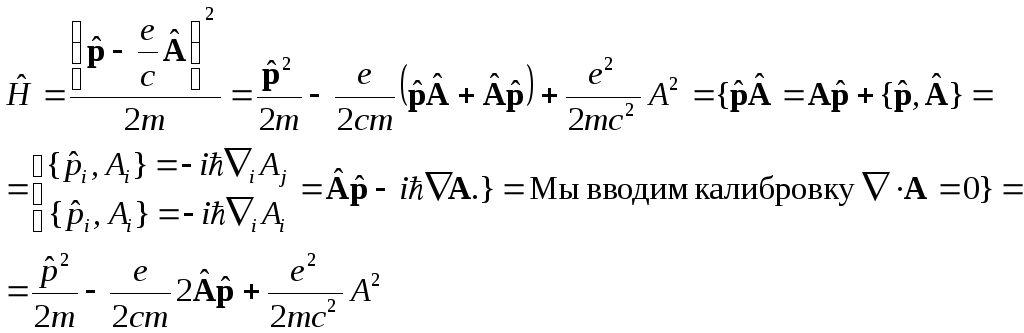
Рассмотрим частный случай – однородное магнитное поле.

Для однородного магнитного поля мы имеем

,

где - напряженность магнитного поля.

Упростим

Здесь

,

оператор момента импульса.

В случае слабого магнитного поля слагаемым можно пренебречь.

Тогда

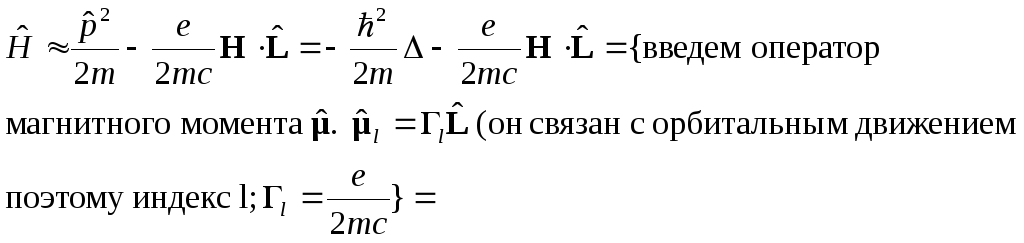
={Если ввести безразмерный момент , тои также вводят магнетон Бора: , тогда }=

=.

Часто направление поля выбирают в качестве направления осиz, где

Тогда