§ 48. Операторы и, и их свойства

Это операторы полного механического момента, они определяются:

Сумма орбитального и спинового моментов.

(это размерный опертор)

Этот опертор обладает всеми коммутационными свойствани, что и опертор , а именно:

1. 

2. 

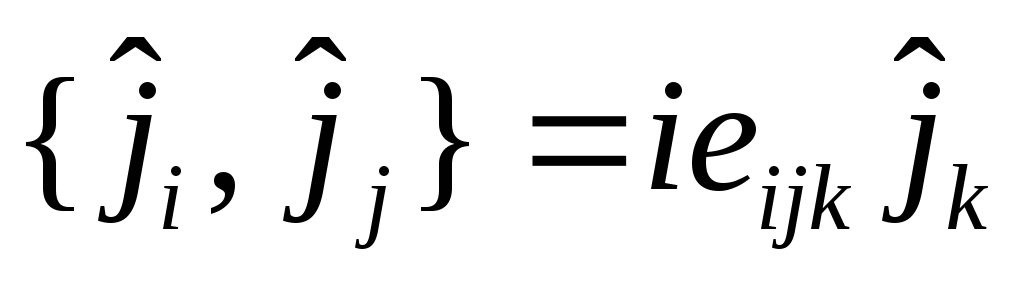
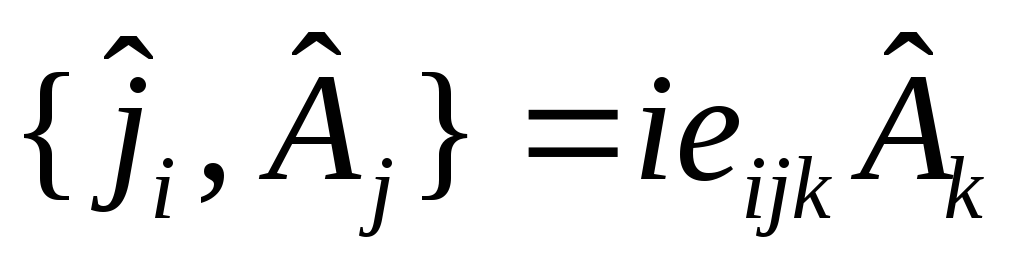
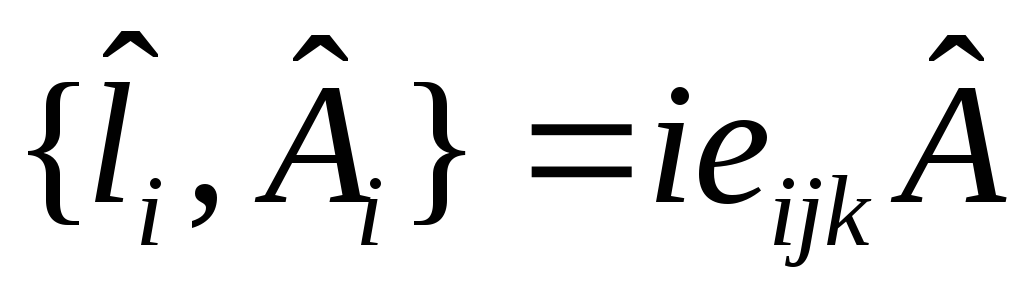3. , тогда 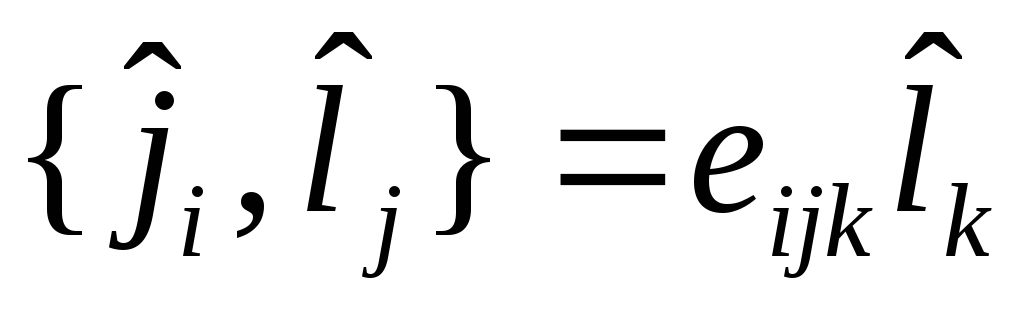. Мы использовали формулу 2, т. к. оператор полного момента осуществляет вращение в пространстве полных переменных .

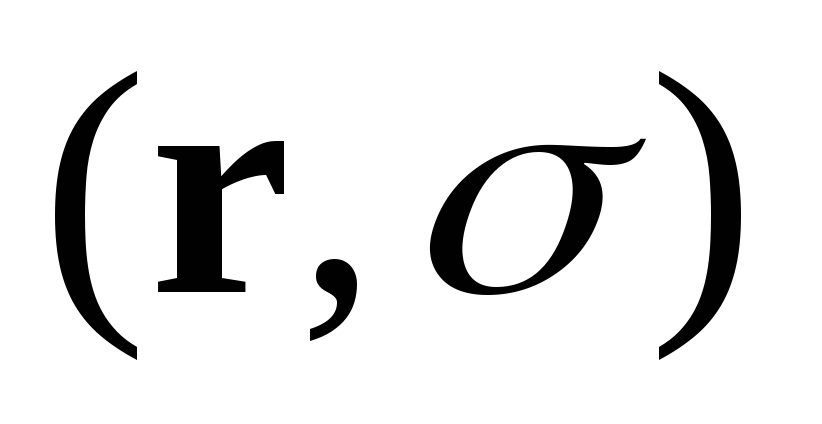4. Z –овая проекция ограничена по закону

,

Так как , а, то выясняется, чтоне пропорционален, т. к. гиромагнитные отношения

Также

Если известно:

и ,

то

§ 49. Тонкая структура атомных уровней (мультиплетность).

При решении задачи о электроне в центральном поле, мы не учитывали дополнительного слагаемого, которое следует из тонкой структуры; это слагаемое называется спин-орбитальным взаимодействием. Это взаимодействие описывается релятивистским оператором .

,

где

В приближении самосогласованного поля

Далее будем писать

Если поместить спиновую частицу в магнитное поле , то получим добавку к энергии

При орбитальном движении электрон будет порождать поле

Но существует спиновый момент

Тогда ибудут взаимодействовать между собой и порождают спин-орбитальное взаимодействие.

Но мы не можем говорить о траектории электрона, тогда спин-орбитальное взаимодействие “размазано” по всему пространству локализации.

Функция

,

где

кулоновский потенциал электрона.

Гамильтониан запишем в виде

, (*)

где - гамильтониан, не учитывающий спин-орбитальное взаимодействие.

Для нахождения энергетических уровней надо решить задачу Штурма-Лиувилля с оператором (*):

(**)

Интегралом движения является полный механический момент .

Интегралы движения называются хорошими квантовыми числами.

Наряду с интегралами движения могут бытьи, когда.

Пусть добавка малая, тогда можно использовать теорию возмущений (т. е. использовать разложение по малому параметру), тогда и энергия из (**) для оператора(*) будет (в разложении до первого члена):

,

где

Здесь оператор без учета спин-орбитального взаимодействия, тогда

Таким образом существует две задачи

(1)

(2)

Решение задачи (2) нам известно, а решение задачи (1) найдем из теории возмущений.

Для (2) энергия квантуется, спектр дискретный, тогда для i-ого уровня имеем ,. Подi понимаем набор квантовых чисел определяющих состояние атома, т. е. n l s m_l m_s

Поскольку атом может содержать много электронов, то энергия может иметь зависимость от первых трех квантовых чисел, поэтому по ним чаще всего не бывает вырождения.

По () кратность вырождения(2l+1).

По () кратность вырождения(2s+1).

Тогда кратность вырождения (2s+1)(2l+1).

Рассмотрим свойства матричных элементов:

,

предполагая, что

.

Тогда

{используем ортонормированность функций}=

Таким образом матрица имеет диагональный вид.

Нахождение собственных значений некоторого оператора сводится к диагонализации матрицы. Если матрицу диагонализировали, то по диагонали стоят собственные значения оператора, а базис образуют собственные функции.

Итак рассмотрим матричные элементы:

,

здесь невозмущенная собственная функция из задачи (2).

Из теории возмущений известно, что в первом приближении i-ый уровень имеет вид

Рассмотрим диагональный элемент спин-орбитального взаимодействия

.

Легко видеть

,

тогда

Разделяя переменные, имеем

,

где - радиальная часть волновой функции.

- это суммирование и интегрирование по.

Рассмотрим вспомогательный вопрос:

,

a и b – номер частицы. Так как a и b разные частицы, то их полные механические моменты одновременно измеримы.

Рассмотрим среднее

Усреднение по некоторому конкретному состоянию дает собственное значения оператора .

.

Найдем

Мы знаем, что

Теперь запишем среднее для :

Вместо ,.

При заданных квантовых числах и, квантовое числоменяется в интервале.

Часто вместо ииспользуюти. Вырождение понаходится: , тогда

Энергетические уровни с учетом спин-орбитального взаимодействия зависят от квантового числа , поэтому производят вышеуказанную замену.

Из вышесказанного ясно, что

.

Здесь нет индекса , т. е. вырождение по этому индексу остается. Кратность вырождения здесь =(2j+1)

Тогда, пусть был уровень

Совокупность этих линий, которые образовались в результате спин-орбитального взаимодействия называется мультиплетом.

Найдем расстояние между двумя соседними уровнями:

{здесь нет разности по l и s, т. к. у мультиплетных линий l и s одинаковые}

Здесь

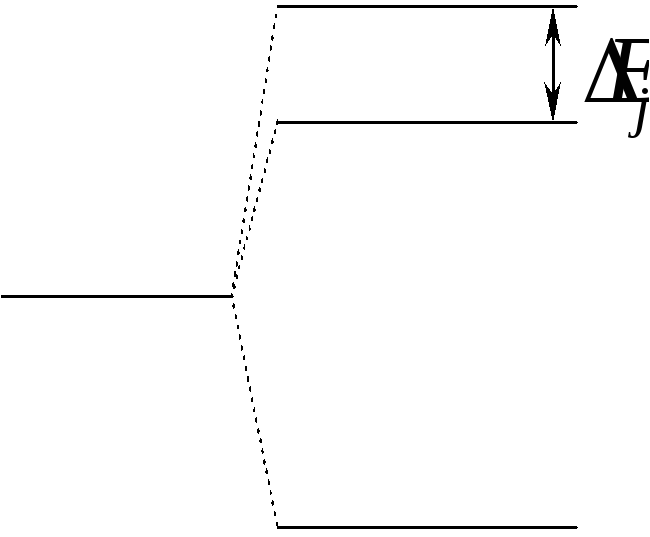
С ростом j энергия в мультиплете возрастает, если A положительное. Это нормальный мультиплет.

Если , то обращенный мультиплет. С ростом энергия в мультеплете падает.

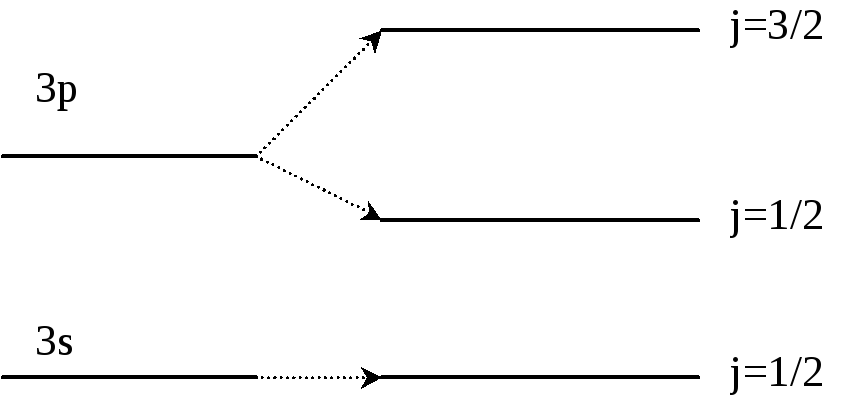
Рассмотрим дублет натрия:

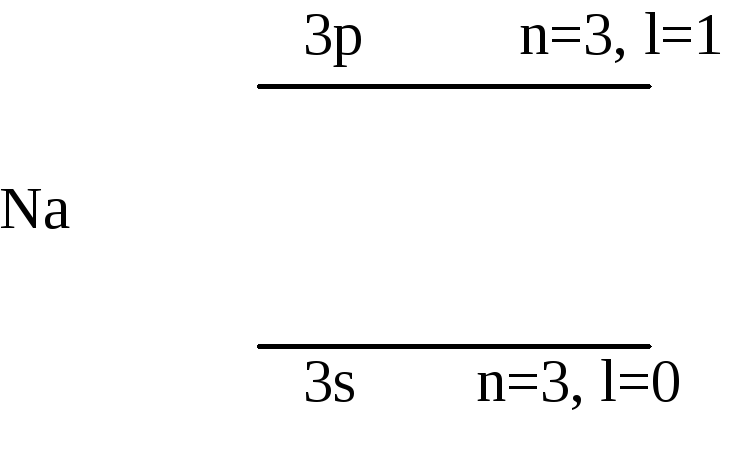
Всю замкнутую заполненную оболочку электронов можно рассматривать как одно большое ядро. Тогда вокруг этого большого ядра вращается свободный электрон.

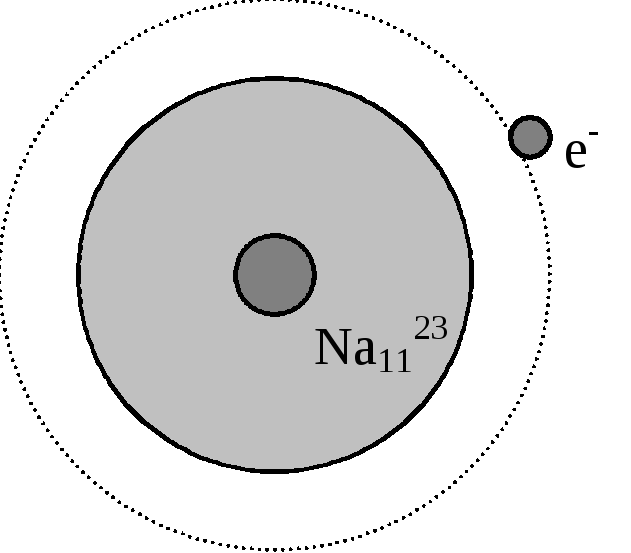
Здесь , так как спин большого ядра равен 0, а спин электрона.

Для уровня : .

.

Здесь расщепление уровня не будет. Этот уровень называется синглетом.

Для уровня 3p: .

Здесь уже два состояния (расщепление уровня на 2).