§132 Функция распределения вероятностей по энергии w(e) и распределение Гаусса.

Поскольку величина относительное среднеквадратичное отклонения для энергии значительно меньше 1:

, то функция распределения этой величины (энергии) описывается узкой функцией с максимумом:

E

Т. к. максимум резкий, то часто апроксимируют эту функцию распределения Гауссовым распределением: -это гауссово

распределение случайной величины x.

Константы илегко находятся:

-из условия нормировки , тогда

интеграл - является табличным.

Тогда

Найдем константу через:

{исп. диф-рование по параметру, где мы обозначим }

тогда

Очевидно, что т. к.

-нечетная функция в симметричных пределах

т. к. четная

Имеется тогда для (1)

Т. к. , то удобно записывать так, чтобы, тогда пишут

(2) (зависимости (1) и (2) разные, это надо

помнить)

где

и говорят

и пишут, что:

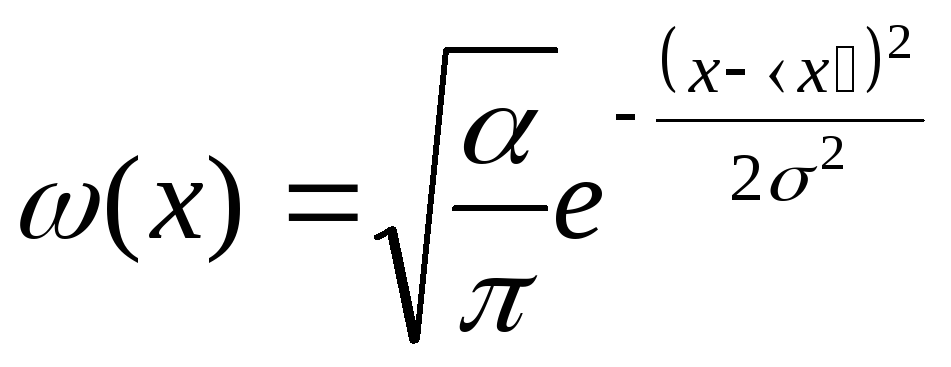
пишут , тогда

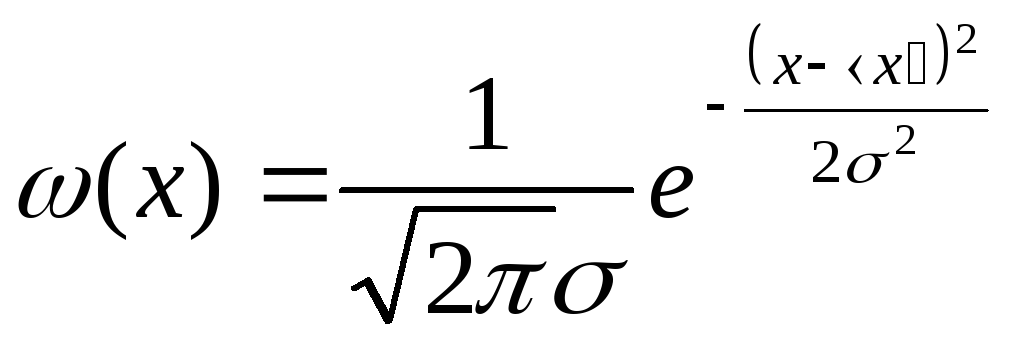получили такой результат

Когда писали- то получали усредненную случ. величину.

Перейдем к нормированным функциям, т. е. перейдем от .

Обозначим , тогдаj тогда

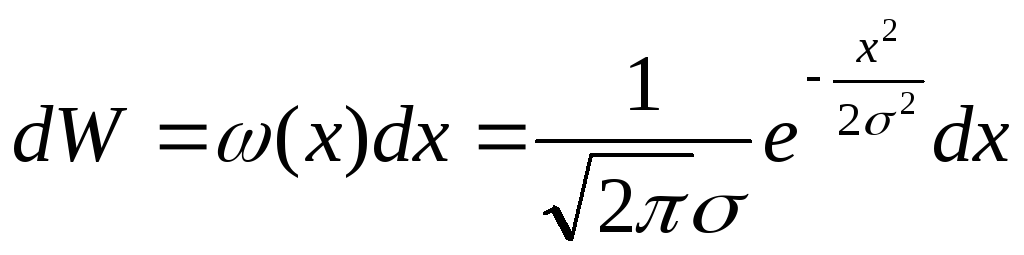
переходят к

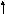здесь у сл. величины y: и

это получили очень

удобную функцию Гаусса,

в ней все удобно считать.

§133 Квазиклассическое приближение в статистической физике.

Мы говорим, что состояние квантово-механической системы в каноническом распределении описывается

, где -номер состояния.

Потом учли что энергетические уровни близко расположены друг к другу и ввести вместо прерывного спектра- непрерывный:

Ввели функцию

Внормировке ф-циипереходит в непрерывное распределение

по состояниям

- число состояний в интервале энергий

где - плотность состояний с энергией, на единичный интервал энергии.

Мы вместо часто пользуемся ф-цией, где

{ где . Ф-ция-размерная, например величиныимеет размерность, тогда объемчикимеет размерностьв степени числа степеней свободы.

А ф-ция имеет обратную этой размерность.

Поэтому удобней ввести величинугде- число степеней

свободы системы}=

здесь уже безразмерные величины

При имеем квазиклассическое приближение.

В этом случае характеризует величину числа состояний в интервале энергий.

Как подсчитать число состояний при переходе из фазового пр-ва в квазиклассическом представлении.

В кв. мех.: - это точность с которой апроксимируется фазовая точка в

фазовом пространстве.

Но фазовая точка определяет состояние, тогда это точность с которой определяется состояние:

- Это площадка, описывающая состояние

- силу принципа неопределенности при переходе , такая площадка выделяется на 1–одну фазовую точку, на одно состояние

(в случае -одна степень свободы).

Тогда - это объем приходящейся на одно состояние в квазиклассическом приближении, при-степеней свободы.

элементарный объем фазового пр-ва

объем на одно состояние (см. выше)

число состояний

Тогда в квазиклассическом приближении в каноническом распределении:

где - статистич. сумма

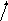
этот множитель возникает по следующим причинам:

вкв. случаесуммирование по числу состояний, и мы

учитывали перестановки не тождественны.

Но интегрирование по фазовому пр-ву (не чувствительно к тождественным перест. – не выбрасывает их) не учитывает тождественных перестановок, поэтому возник множитель - учитывающий тождественные перестановки. Это имеет место при переходе в квазиклассическое приближение.

Замечание: Принцип тождественности оказывает влияние только на расчет статистического интеграла ,

При расчете средних это не влияет.

Канонич. распределение для кв. систем имеет вид

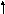где - номер кв. состояния систем

суммир. По кв. состоянием системы

При переходе в квазиклассику, используя переход, получаем для вероятности состояния(здесь индекс не поставлен):

их здесь штук.

Здесь -число степе-

ней свободы

, где

и

- это вероятность того, что фазовая точка с координатами попадет в элементарный фазовый объемв фазовом пространстве

и мы писали

под понимаем:

Очевидно, что константу можно выкинуть, если рассчитывать среднее через вероятность, при переходах:

т. к. константа не влияет на расчет средних.

Часто рассматриваем случай когда квазиклассичность имеет место не по всем степеням свободы, а лишь по некоторым. Тогда суммируем по кв. степеням свободы и интегрир. по квазикласс. степеням свободы, тогда имеют гибрид: , тогда имеется и стат. интеграл и стат. сумма.

154