§125 Микроканоническое распределение Гиббса. Рассмотрим замкнутую систему, и согласно принципу равной вероятности, все состояния системы, с заданной энергией , равновероятны.

Причем, т. к. система находится в состоянии со средним значением энергии , то

Для того чтобы получить распределение, учитывающее флуктуации, мы исп. Теорему Лиувилля и перейдем к Каноническому распределению Гиббса

§126 Каноническое распределение Гиббса.

Удобно записать т. Лиувилля в виде, что есть интеграл движение, т. е.- есть функция различных интегралов движения.

Поместим систему в жесткий неподвижный ящик. Тогда т. к. система не может двигаться у них нет сравнения импульса, а т. к. не может

вращаться, то нет сохранения момента импульса. Тогда осталось сохранения энергии, т. е. можем записать .

Само распределении пишется:

-это каноническое распределение Гиббса

с- константа не зависящая от состояния , которая находится из условия.

Для квантового случая повышается -номер кв. состояния.

Здесь - температура в энергетической шале- это удобно в теории; хотя на практикеизмеряют в градусах.

Нам требуется 2-ое начало термодинамики, т. е. принцип возрастания энтропии

тогда

§127 Принцип возрастания энтропии.

Наиболее вероятным развитием системы является такое, при котором полная производная энтропии больше 0: (*)

это сформулировано Клаузиусом.

Имея этот принцип, можем получить соответствующее распределение.

Условие (*) означает, что если система выведена из состояния равновесия, то она движется к равновесию по закону (*).

Тогда в состоянии равновесия энтропия системы экстремально (max).

Т. к. условие нормировки имеется, то имеем условный экстремум, а если бы не было условия нормировки, то был бы абсолютный экстремум.

Добавление к т. Лиувилля

В случае квазизамкнутых статистически независимых систем мы писали для плотности вероятности:

, где - индекс подсистемы.

На языке классических функций мы писали

это следствие статистической независимости подсистем.

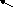{Для кв. случая пишутиндекс подсистемы

номер кв. состояния }

тогда , т. е. логарифместь аддитивная величина.

Из т. Лиувилля имели , т. е.-есть интеграл движения,

т. е. можно получить как суперпозицию интегралов движения.

Для квазизамкнутых подсистем (в частном случае) имеем - интеграл движения, а- аддитивная величина, тогдаможно представить как суперпозицию аддитивных интегралов движения.

В большинстве случаев ограничиваются одним из семи интегралом движения, а именно энергией. Поэтому для -той подсистемы можем записать:

здесь 7 интегралов движения

-энергия (один)

-энергия (три)

- момент кол-ва движения (три)

Когда систему помещаем в жесткий ящик, где она не может вращаться или перемещаться, то зависимость отиисчезает и остается только зависимость(*)

Где и- произвольные.

В силу макроскопичности системы, то влияние граничных условий ящика на общее термодинамическое состояние не оказывает воздействие, а влияет лишь в тонком приграничном слое.

В кв. случае, можно связать с,

где -это коэффициенты разложения волновой функции по собственным волновым функциям оператора Гамильтона (оператора энергии).