§115 Два способа усреднения в стат физике.

Рассмотрим стационарные процессы, и рассмотрим случайную величину А(t), где t – время, это одна переменная.

Усреднение по времени проводим так: {A} = =

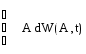
Если случайная величина А – случайная, то ее усреднение соответствует усреднению по фазовой траектории в фазовом пространстве.

Зависимость координат от времени в фазовом пространстве определяется фазовой траекторией.

A[,] = А(t)

Усреднение по времени имеет основой эксперимент, т. к. экспериментатор наблюдает сл. Величину во времени. В этом определении усреднения постулируются только Назовем τ – временем релаксации. Если Т >> τ, то этот предел

_{хорошо согласуется с практикой.}

_{И принимают Анаблюд = {A}}

_{Усреднение по времени однако неудобно в теории, это усреднение по одной реализации.}

_{Другое усреднение – статистическое – оно основано на усреднении случайной величины А как функции p и q.}

_{Каждой точке фазового пространства ставится в соответствие величина А (как функция p и q).}

_{Потом вводится вероятность попадания этой точки в элементарный объем фазового пр-ва:}

_dW(p,q)

_{Легко предположить, что dW(p,q) = ρ(p,q)dГ dV(p,q)}

_{где dV(p,q) = dГ = dpdq – эл. объем фазового пр-ва.}

_{Говорят, что ρ(p,q) – это функциия распределения, определяющая плотность вероятности попадания точки в эл. объем.}

_{И вводится понятие статистического среднего, или среднего по ансамблю.}

_{<A> = ⌠A(p,q)ρ(p,q)dГ dV(p,q)}

_{усредним по фазовому пр-ву.}

§116 Понятие ансамбля систем.

Говорят об ансамбле т.к. каждой точке фазового пр-ва можно поставить в соответствие некоторую траекторию, на которой находится эта точка.

Предполагая, что имеем совокупность макроскопических идентичных систем, именуемых ансамблем; то можем говорить что конкретная точка фазового пространства соответствует конкретному состоянию одной из систем этого ансамбля.

У систем может быть различное динамическое состояние точек, т.к. точки перемещаются в пространстве; хотя число точек, поля и т.п. у систем будут одинаковыми. Это и будет ансамблем, если таких систем будет неограниченно много. Это и есть усреднение по ансамблю.

Рассмотрим стационарные процессы, фазовая траектория очень длинная (бесконечная), тогда говорят, что фазовую траекторию, при рассмотрении предела _,

_{можно разбить на достаточно длинные траектории которым можно приписать системы из ансамбля. Это была гипотеза.}

§117 Эргодическая гипотеза.

_{Согласно эргодич. гипотезе, для наблюдаемых величин в стат физик, вводится:}

_{<A> = {A}}

_{< > = { }}

_{Процессы или поля для которых удовлетворяет это равенство называют эргодическими.}

< > - это усреднение по пр-ву реализаций, где А(r) случ. поле, т.к. здесь больше одной переменной у А.

{ } – усредние по аргументам, которые сидят в А

A(t) – это случ. процесс, т.к. одна переменная у А.

§118 Равновесное состояние у системы.

Для стационарных процессов в случае систем с большим числом степеней свободы обнаруживается (где процесс – A(t)), что в процессе измерения величины А оказывается, что она основное время пребывает в состоянии, имеющем значение близкое к числу <A>, которое практически не отличается от <A>.

Система длительное время пребывает в состоянии со значением <A>.

Это значение представляется, таким образом, наиболее вероятным значением сл. вел. А Состояние системы, описываемое наиболее вероятными значениями макропараметра, называется равновесным. Стационарная макросистем основное время пребывает в основном состоянии, хотя бывают кратковременные флуктуации.

В термодинамике, во всех термодинамических соотношениях, используются равновесные состояния, например, под Е понимают <E>

Пишут Е, подразумевают <E>.