
- •Квантовая механика
- •§ 1. Экспериментальные основы квантовой механики
- •§ 2. Классическое и квантовое описание системы.
- •§ 3 Принцип неопределенности.
- •§ 4. Полный набор динамических переменных
- •§ 5. Постулаты квантовой механики.
- •§ 6 Роль классической механики в квантовой механике
- •§ 7 Волновая функция и ее свойства.
- •§ 8 Принцип суперпозиции состояний
- •§ 9 Понятие о теории представлений
- •§ 10 Операторы в квантовой механике
- •§ 12 Среднее значение измеряемой величины.
- •§ 13 Вероятность результатов измерения
- •§ 14 Коммутативность операторов и одновременная измеримость физических величин
- •§ 15. Операторы координаты , импульса, момента импульса, энергии.
- •§ 16. Решение задачи Штурма-Лиувилля для оператора .
- •§ 17 Решение задачи Штурма-Лиувилля для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы .
- •§ 19 Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в кв. Механике.
- •§ 22. Свойства операторов вида
- •§23. Флуктуации физических величин.
- •§ 24. Неравенство Гайзенберга.
- •§ 25 Оператор Гамильтона различных систем.
- •§ 26. Стационарное состояние различных систем
- •§ 27. Решение волнового уравнения в случае свободной материальной точки
- •Для трехмерного случая
- •§ 28. Интегральные операторы в квантовой механике.
- •§ 29. Интегральный оператор канонического преобразования.
- •§ 30. Каноническое преобразование оператора.
- •§ 31. Уравнения Шредингера в матричной форме.
- •§ 32. Линейный гармонический осциллятор
- •Предельные технологические размеры кристаллов и.С. 0.1 – 0.5 мкм. Существует и предел по физической работоспособности. Однако с уменьшением размера кристалла увеличивается быстродействие приборов.
- •§ 30.1. Каноническое преобразование оператора. Ч. 2
- •§ 34. Унитарные инварианты в квантовой механике.
- •§ 35. Вид операторов ив декартовых и сферических координатах.
- •§ 36. Коммутационные соотношения с оператором .
- •§ 37. Собственные функции и собственные значения операторов и.
- •§ 38. Вырождение энергетических уровней частицы, движущейся в центральном поле.
- •§ 39. Гамильтониан частицы без спина, движущейся в магнитном поле.
- •§ 40. Снятие вырождения по квантовому числу m в случае частицы без спина, движущейся в магнитном поле. Используем
- •§ 41. Оператор бесконечно малого поворота без учета спина.
- •§ 42. Собственный механический момент (спин).
- •§ 43. Операторы ии их свойства.
- •§ 44. Спиновая переменная волновой функции
- •§ 45. Матрицы Паули и их свойства.
- •§ 46 Понятие о спинорах
- •§ 47. Уравнение Паули Мы писали волновое уравнение в виде
- •§ 48. Операторы и, и их свойства
- •§ 50. Принцип тождественности.
- •§ 51. Оператор перестановки и его свойства
- •§ 52. Симметричное и антисимметричное состояния.
- •§ 53. Обменное взаимодействие
- •§ 54. Основное состояние атома гелия
- •§ 55. Схема Юнга квантовой механики.
- •1. И ,
- •2. И .
- •§ 56. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения.
- •§ 58 Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближения.
- •§ 59. Критерий применимости теории возмущений.
- •§ 60. Стационарная теория возмущений в случае близких энергетических уровней.
- •§ 61. Метод (представление) Шредингера. Оператор эволюции и его свойства.
- •§ 62. Метод (представление) Гейзенберга. Уравнение движения для оператора.
- •§ 63. Уравнение эволюции среднего значения физической величины. Соотношение неопределенности: время – энергия.
- •§ 64. Матричное представление операторов.
- •§ 65. E – представление.
- •§ 66. Уравнение Шредингера в матричной форме.
- •§ 67. Матричная формулировка задачи о линейном гармоническом осцилляторе.
- •§ 68. Расчет матричных элементов операторов .
§ 40. Снятие вырождения по квантовому числу m в случае частицы без спина, движущейся в магнитном поле. Используем
![]() ,
,
где
![]()
Для
![]() имеем
имеем
![]()
С учетом магнитного поля, получим
![]()
Это решение получено в первом приближении теории возмущения.
Получилась зависимость энергетических уровней от квантового числа m, т. е. снимается выраждение по m.
§ 41. Оператор бесконечно малого поворота без учета спина.
Рассмотрим
как меняется функция
![]() при вращении координат.
при вращении координат.
При
бесконечно малом повороте координат
на угол
![]() любой вектор, в том числе и
любой вектор, в том числе и
![]() получает
приращение
получает
приращение
![]() .
.
![]()
Тогда
возникает изменение волновой функции
![]()
![]()
Учитывая
малость
![]() запишем разложение в ряд
запишем разложение в ряд![]() по малому параметру.
по малому параметру.
Общее соотношение:
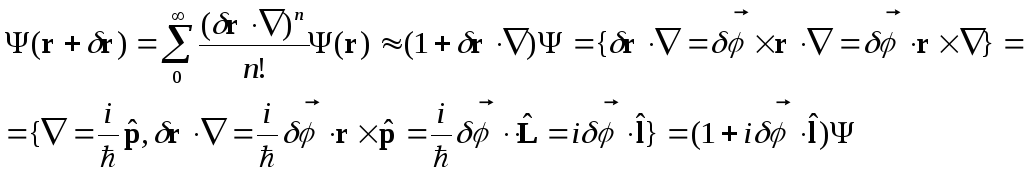
Оператор бесконечно малого поворота
![]()
Если рассматривать вращение вокруг оси z, то
![]() .
.
Тогда
![]()
Если
![]() -
собственная функция оператора
-
собственная функция оператора![]() ,
то для этой функции имеем
,
то для этой функции имеем
![]()
Если проинтегрировать по углу поворота, то
![]() .
.
Вывод:
Оператор
![]() - обеспечивает операцию вращения в
пространстве, он действует на координату
- обеспечивает операцию вращения в
пространстве, он действует на координату![]() .
.
§ 42. Собственный механический момент (спин).
Рассмотрим Na. У него есть желтая линия . Возникает при переходе с уровня 3p на 3s.
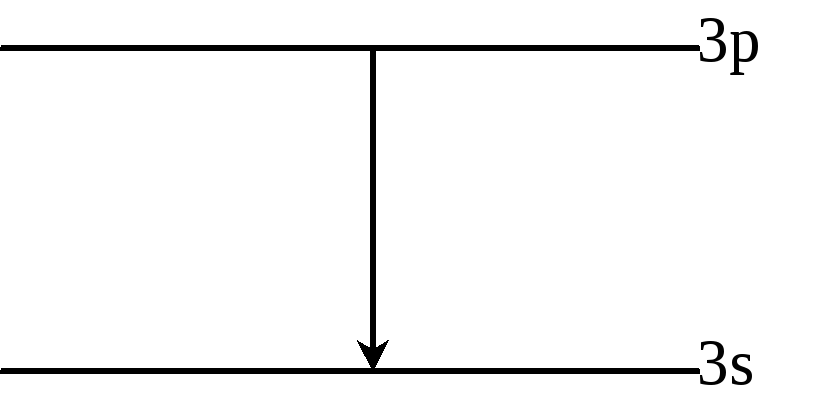
Первоначально
ее длина была 5892
![]()
Было обнаружено, что эта линия расщепляется на две: дублет.
Возникла идея расщепления уровня 3p на два, тогда можно объяснить возникновение двух линий.
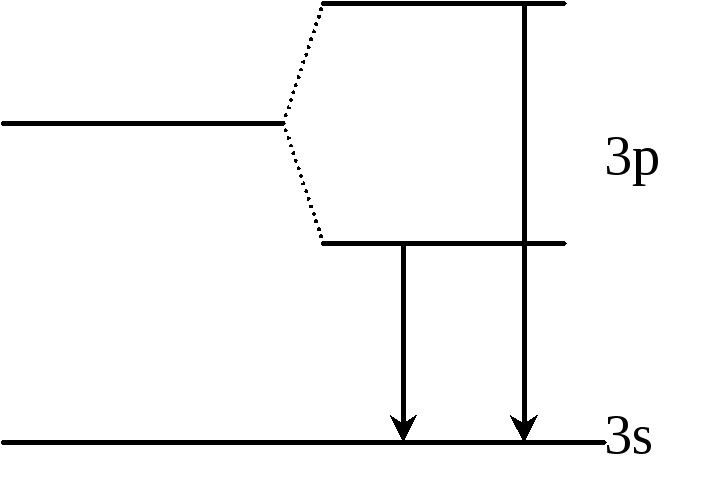
Их
длины: 5896
![]() и 5890
и 5890![]() .
.
В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента.
У
электрона спиновое число s=![]() .
.
Впоследствии Паули ввел спин в теорию.
Если
имеем одну частицу, то она характеризуется
орбитальным квантовым числом
![]() .
.
Состовная
частица (атом) состоит из многих
микрочастиц. Можно рассматривать эту
составную частицу вцелом и приписать
ей момент
![]() ,
который описывает орбитальное движение
частицы как целого.
,
который описывает орбитальное движение
частицы как целого.
Энергетический
уровень этой составной частицы в
некоторых полях будет зависеть от
орбитальных моментов микрочаститц
![]() .
.
Эти моменты являются внутренним свойством этой составной частицы.
Можно рассматривать 2 момента:
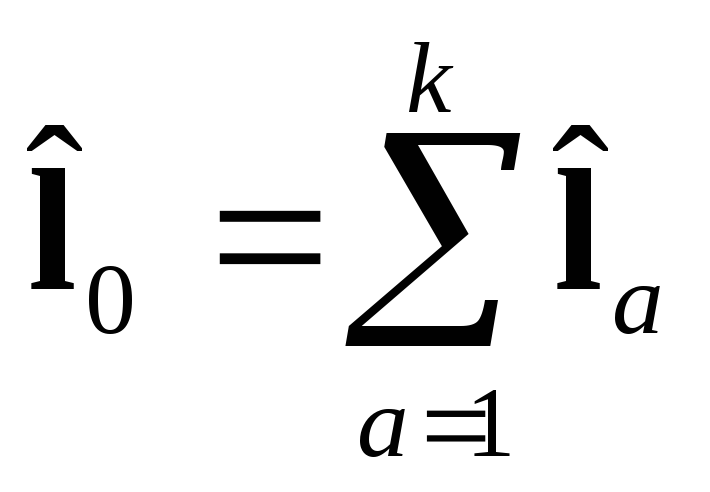 .
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)
.
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)Частица сама движется по некоторой траектории.
У
частицы есть еще квантовое число
![]() ,
характеризующее собственный механический
момент.
,
характеризующее собственный механический
момент.
Вводят оператор собственного механического момента:
![]()
По аналогии
![]()
Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы.
§ 43. Операторы ии их свойства.
Все
проводится по аналогии с
![]() и
и![]() .
.
![]() обладает
коммуникационными свойствами:
обладает
коммуникационными свойствами:
![]()
Так
как
![]() и
и
![]() не коммутируют, то они ондновременно
не измеримы.
не коммутируют, то они ондновременно
не измеримы.
Но
![]() .
.
Собственные значения оператора:
![]() ,
, ![]() .
.
Тогда здесь всего 2s+1 значение оператора.
Перейлем
к классическому пределу:
![]()
Ввиду
связи
![]() имеем
имеем![]() ,
,![]() .
.
Ясно,
что так как
![]() - параметр частицы, то он не меняется ни
при каких условиях, тогда в классическом
пределе:
- параметр частицы, то он не меняется ни
при каких условиях, тогда в классическом
пределе:
![]() ,
, ![]() .
.
В классической механике этим величинам аналога нет и они обращаются в нуль.
В
случае спина мы не можем наложить условие
![]() ,
т. к. спин – внутреннее свойство частицы.
Тогда
,
т. к. спин – внутреннее свойство частицы.
Тогда![]() не всегда целое число.
не всегда целое число.
Если
![]() - четное, то
- четное, то![]() -полуцелое.
-полуцелое.
Если
![]() - нечетное, то
- нечетное, то![]() -целое.
-целое.
Отсюда деление на 2 типа частиц:
Фермионы – спин полуцелый
Бозоны – спин целый.
