
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
Вопрос32.Функции и отображения. Предел, непрерывность.
Определение
32.1
Функция
![]() сопоставляет элементам множества
сопоставляет элементам множества![]() ( называемого областью определения)
числа
( называемого областью определения)
числа![]() .
.
Определение
32.2
Отображение
![]() сопоставляет
элементам множества
сопоставляет
элементам множества![]() элементы
элементы![]() .
.
Таким
образом, функция – это частный случай
отображения
![]() .
Задать отображение – это все равно, что
задать
.
Задать отображение – это все равно, что
задать![]() функций
функций
![]()
![]()
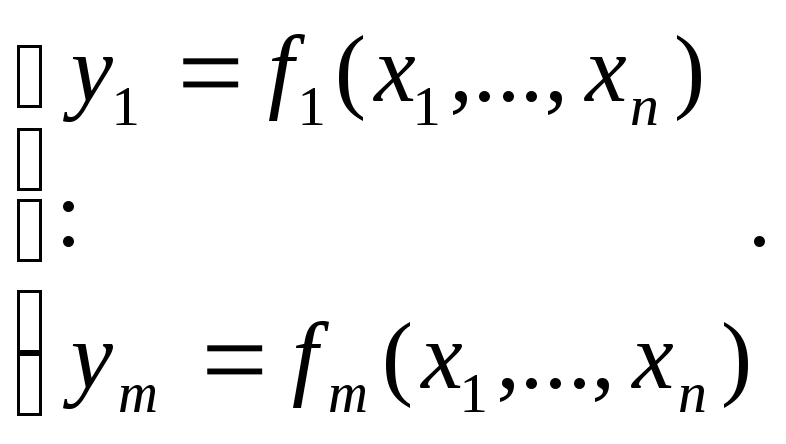
Примеры.
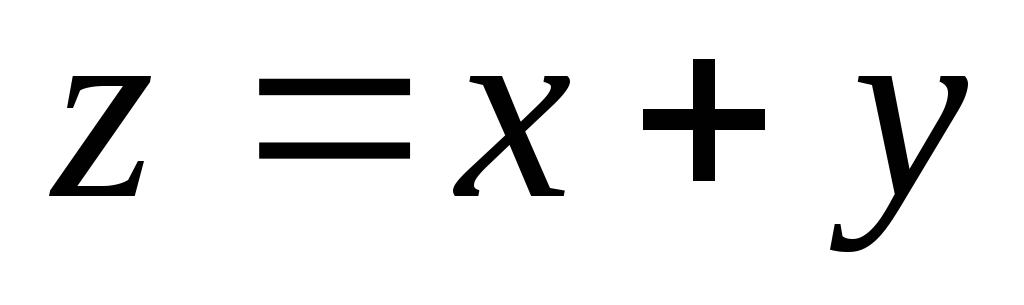 -
функция двух переменных, паре
-
функция двух переменных, паре
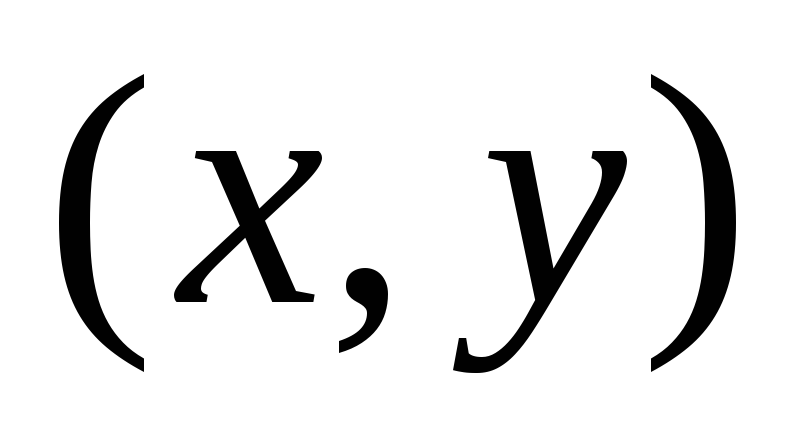 сопоставляет число
сопоставляет число .
.Отображение

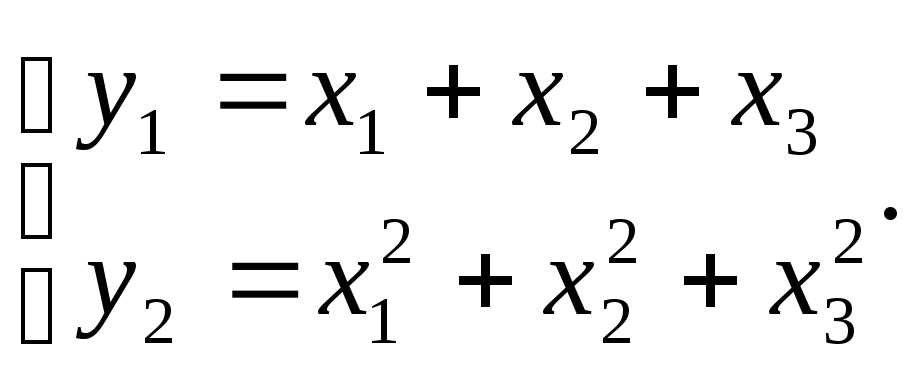
Вектор-функция
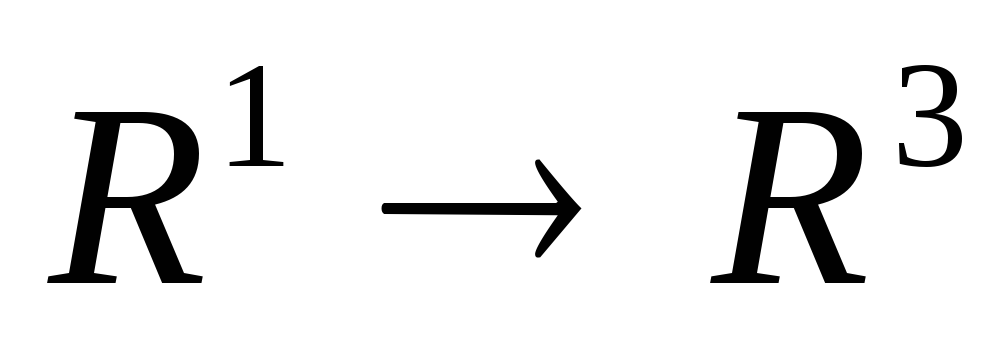
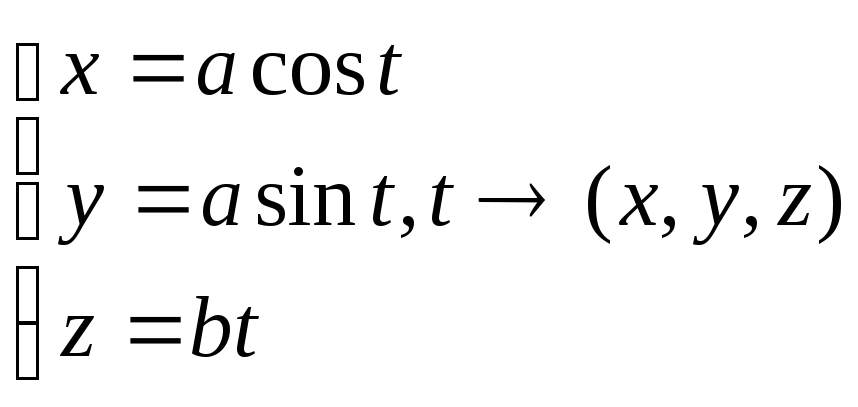 Винтовая
линия.
Винтовая
линия.
Пусть
![]() - предельная точка области определения
- предельная точка области определения![]() .
.
![]()
![]()
![]()
![]()
“Конкретизируя”
окрестности, это определение в метрических
пространствах
![]()
![]()
![]()
![]() ,
или, для
,
или, для![]()
![]()
![]()
![]()
![]() Или
Или
![]()
![]()
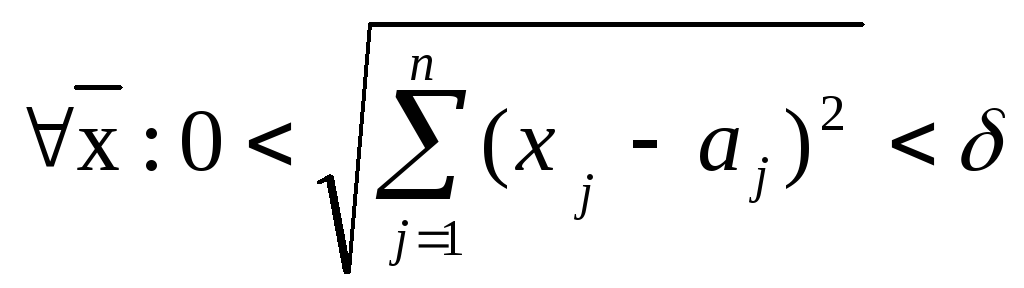 выполняется
неравенство
выполняется
неравенство
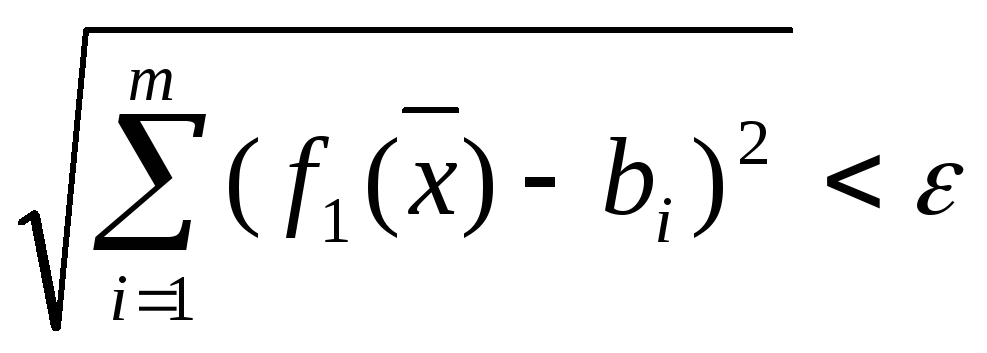 (17.1)
(17.1)
Теорема
32.1.
![]()
![]() .
.
Доказательство.
![]() Поскольку
Поскольку
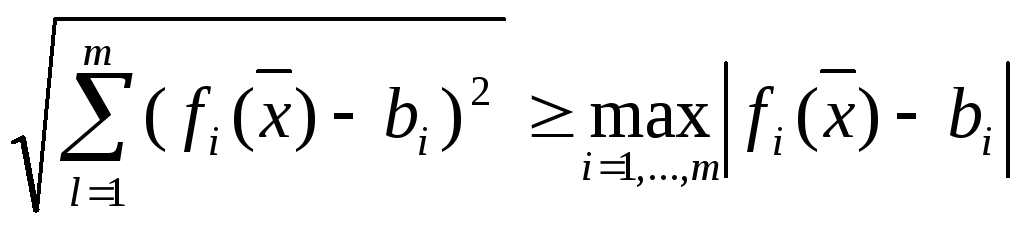 ,
из (17.1) следует, что
,
из (17.1) следует, что![]() при
при![]() .
Но это как раз и означает, что
.
Но это как раз и означает, что![]() .
.
![]() .
Пусть
.
Пусть
![]() - фиксировано. Выберем
- фиксировано. Выберем![]() так, чтобы при
так, чтобы при![]() выполнялось неравенство
выполнялось неравенство![]() Взяв
Взяв![]() получаем, что при
получаем, что при![]() выполняется неравенство
выполняется неравенство
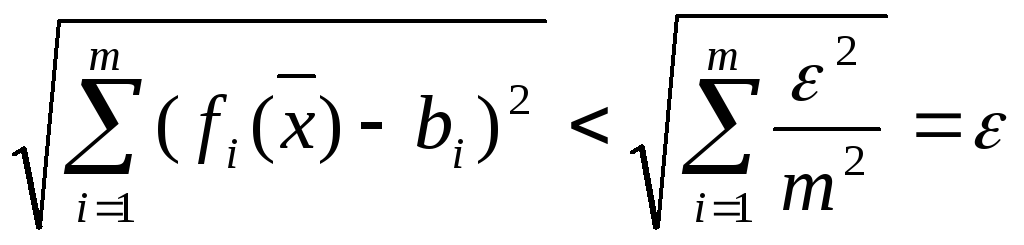 .
.
Определение
32.3.
Отображение
![]() непрерывно
в точке
непрерывно
в точке
![]() ,
если
,
если![]()
Согласно
сказанному выше, непрерывность отображения
![]() равносильна непрерывности всех функций
равносильна непрерывности всех функций![]() .
.
Так же, как и в случае функций одной переменной, справедлива следующая теорема.
Теорема
32.2.Если
![]() ,
то
,
то![]() ,
,![]() ,
и если
,
и если![]() ,
то
,
то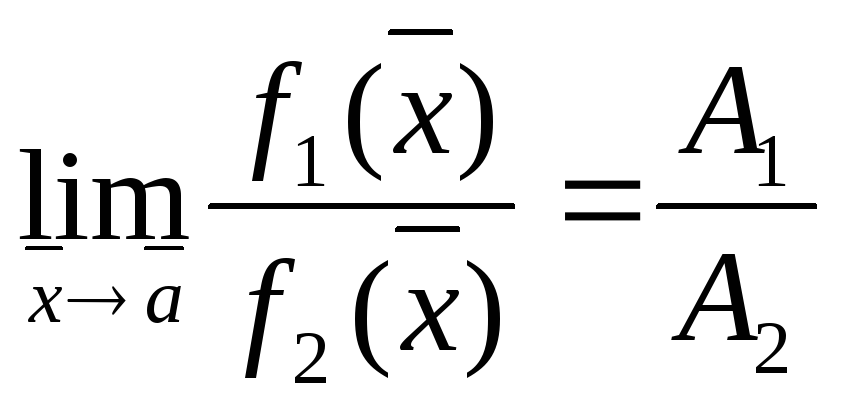 .
.
Следствие.
Сумма, разность, произведение и частное
( при
![]() )
непрерывных функций
)
непрерывных функций![]() и
и![]() являются непрерывными функциями.
являются непрерывными функциями.
Теорема
32.3.
Если
![]() непрерывно в точке
непрерывно в точке![]() ,
отображение
,
отображение![]() непрерывно в точке
непрерывно в точке![]() ,
то отображение
,
то отображение![]() непрерывно в точке
непрерывно в точке![]() .
.
Доказательство.
Для всякой окрестности
![]() существует
существует![]() такая, что
такая, что![]()
![]() .
Но
.
Но![]()
![]()
![]() .
Эта окрестность
.
Эта окрестность
![]() - искомая, т.к.
- искомая, т.к.
![]() .
.
Теорема
32.4.
(Теорема о сохранении знака непрерывной
функции). Если
![]() то
то![]()
![]() .
.
Доказательство.
Достаточно доказать, что если
![]() ,
то и
,
то и![]() .
Действительно, взяв
.
Действительно, взяв![]() получаем по определению непрерывности
окрестность
получаем по определению непрерывности
окрестность
![]() такую
что
такую
что
![]()
![]() .
.
Теорема 32.5. Непрерывный образ компактного множества есть компактное множество. (без доказательства).
Замечание. Эта теорема непосредственно обобщает теоремы 1 семестра о том, что непрерывная на отрезке функция ограничена и достигает наибольшего и наименьшего значений.
Теорема 32.6. Непрерывный образ связного множества (т.е. множества, любые 2 точки которого можно соединить кривой, целиком лежащей внутри этого множества) есть связное множество. (без доказательства).
Замечание. Эта теорема обобщает теорему 1 семестра о том, что непрерывная на отрезке функция принимает все свои промежуточные значения.
Теорема
32.7.
(Теорема Кантора). Непрерывная на компакте
![]() функция равномерно непрерывна на нем,
т.е.
функция равномерно непрерывна на нем,
т.е.![]()
![]()
![]()
![]() .
.
Функции Кобба-Дугласа.
Функция
Кооба-Дугласа имеет вид
![]() ,
где
,
где![]() -
величина произведённого продукта,
-
величина произведённого продукта,![]() - затраты труда,
- затраты труда,![]() - объём производственных фондов,
- объём производственных фондов,![]() - коэффициенты.
- коэффициенты.
Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
Пусть
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() ,
,![]() - точка из этой окрестности.
- точка из этой окрестности.
Определение
33.1
Величина
![]() называетсяприращением
функции
называетсяприращением
функции
![]() в точке,
в точке,
![]() соответствующим
приращению аргумента
соответствующим
приращению аргумента
![]() .
.
Определение
33.2
Функция
![]() называетсядифференцируемой
в точке
называетсядифференцируемой
в точке
![]() ,если
существуют такие постоянные числа
,если
существуют такие постоянные числа
![]() и
функции
и
функции
![]() при
при
![]()
![]() (18.1)
(18.1)
Часто
обозначают
![]() и
и
![]() .Тогда
(18) перепишем в виде
.Тогда
(18) перепишем в виде
![]() .
.
При
![]() наше определение (18.1) совпадает с
известными из материала 1-го семестра
определением дифференцируемости
наше определение (18.1) совпадает с
известными из материала 1-го семестра
определением дифференцируемости![]() .
Для функций одной переменной
дифференцируемость равносильна
существованию производной. В случае
нескольких переменных ситуация несколько
сложнее.
.
Для функций одной переменной
дифференцируемость равносильна
существованию производной. В случае
нескольких переменных ситуация несколько
сложнее.
Сначала
введем в рассмотрение величину
![]() .
Она представляет собой приращение
функции при фиксированных значениях
всех производных, кромеi-той.
.
Она представляет собой приращение
функции при фиксированных значениях
всех производных, кромеi-той.
Пусть
![]() дифференцируема в точке
дифференцируема в точке
![]() .Тогда
для любого
.Тогда
для любого
![]() равенство
(18.1) дает
равенство
(18.1) дает
![]() при
при![]() (18.2)
(18.2)
Поскольку
![]() при фиксированных значениях
при фиксированных значениях![]() равносильно тому, что
равносильно тому, что![]() ,
равенство (18.2) означает, что функция
одной переменной
,
равенство (18.2) означает, что функция
одной переменной![]() .
.
![]() дифференцируема
в точке
дифференцируема
в точке
![]() и, значит, существует
и, значит, существует![]()
![]() (18.3)
называемый, по определению, частной
производной функции
(18.3)
называемый, по определению, частной
производной функции
![]() по переменной
по переменной![]() в точке
в точке
![]() .
.
Мы только что, тем самым, доказали теорему:
Теорема
33.1.
Если
![]() дифференцируема в точке
дифференцируема в точке
![]() ,то
для всех
,то
для всех
![]() существуют
существуют
![]() .
.
Таким
образом, существование частных производных
– необходимое
условие
дифференцируемости. При этом
![]()
![]() при
при
![]() .
.
Другое необходимое условие дифференцируемости – непрерывность функции, как показывает следующая теорема.
Теорема
33.2.
Если
![]() дифференцируема в точке
дифференцируема в точке
![]() ,то
,то
![]() .
.
Доказательство.
Достаточно
доказать, что при
![]() ,
,
![]() ,
(т.к.
,
(т.к.![]() ).
Но это сразу следует из равенства (18.1),
так как
).
Но это сразу следует из равенства (18.1),
так как![]() .
.
Однако,
в отличие от случая
![]() ,
из существования частных производных
,
из существования частных производных
![]() ,определенных
равенством (18.3)не
следует
даже непрерывность функции
,определенных
равенством (18.3)не
следует
даже непрерывность функции
![]() в точке
в точке
![]() и
тем более не следует дифференцируемость
и
тем более не следует дифференцируемость
![]() в точке
в точке
![]() ,согласно
теореме(18.2).
,согласно
теореме(18.2).
Пример.
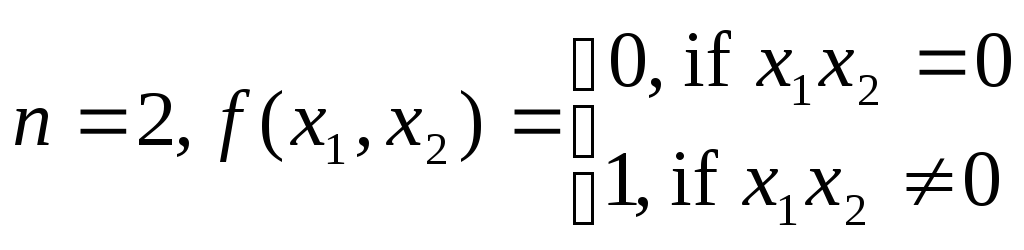 .
Тогда
.
Тогда![]() ,
так как
,
так как
![]() .Аналогично,
.Аналогично,
![]() .Однако
.Однако
![]() даже
не непрерывна в точке
даже
не непрерывна в точке
![]() .
.
Достаточное условие дифференцируемости дает следующая теорема.
Теорема
33.3.
Пусть частные производные
![]() существуют в окрестности точки
существуют в окрестности точки
![]() и
непрерывны в этой точке. Тогда
и
непрерывны в этой точке. Тогда
![]() дифференцируема в точке
дифференцируема в точке
![]() .
.
Доказательство.
Пусть
![]() принадлежит рассматриваемой окрестности
принадлежит рассматриваемой окрестности
![]() .При
этом все точки
.При
этом все точки
![]() так же принадлежат рассматриваемой
окрестности. Приращение функции
так же принадлежат рассматриваемой
окрестности. Приращение функции
![]() представим в виде
представим в виде![]() (4)
(4)
и
рассмотрим разности
![]() (5)
составляющие
в сумме приращение (4).
(5)
составляющие
в сумме приращение (4).
Положим
![]() (то
есть фиксируем все переменные, кроме
(то
есть фиксируем все переменные, кроме![]() ).
Тогда рассматриваемая разность (5) имеет
вид
).
Тогда рассматриваемая разность (5) имеет
вид![]() .
Функция
.
Функция![]() по условию дифференцируема на отрезке,
соединяющим
по условию дифференцируема на отрезке,
соединяющим![]() и
и![]() .
Значит, она непрерывна на этом отрезке
и можно применить теорему Лагранжа,
согласно которой
.
Значит, она непрерывна на этом отрезке
и можно применить теорему Лагранжа,
согласно которой![]() ,
где
,
где![]() .
.
Но
![]() .
По условию непрерывности частных
производных
.
По условию непрерывности частных
производных![]() ,
где
,
где
![]() при
при
![]() .
.
Поэтому
каждая из разностей (5) имеет вид
![]() ,
а приращение (4) совпадает с (3) из
определения дифференцируемости. Теорема
доказана.
,
а приращение (4) совпадает с (3) из
определения дифференцируемости. Теорема
доказана.
Замечание
1.
Непрерывность частных производных не
является необходимым условием
дифференцируемости функций. Например
можно доказать, что функция
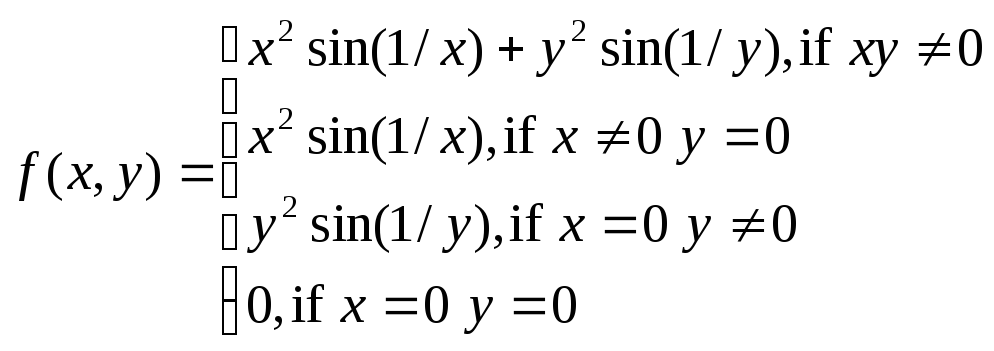 дифференцируема в точке
дифференцируема в точке
![]() ,
но частные производные в этой точке не
непрерывны.
,
но частные производные в этой точке не
непрерывны.
Замечание
2.
Тем не менее, для функции
![]() частные производные в точке
частные производные в точке
![]() равны
0, так как
равны
0, так как
![]() и
и![]() (в остальных точках
(в остальных точках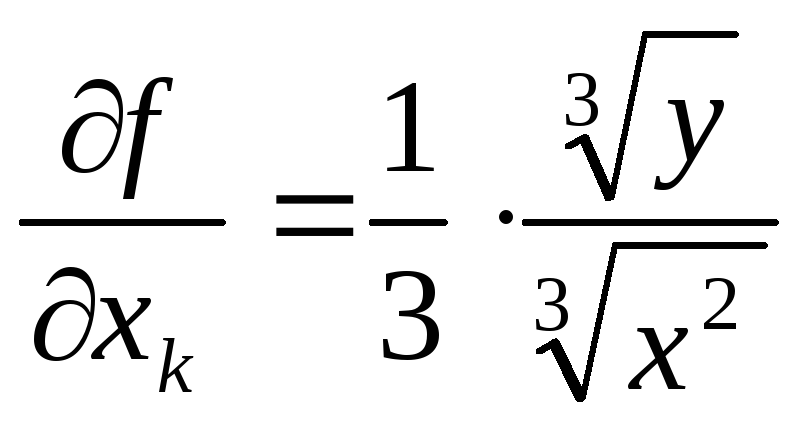 ,
,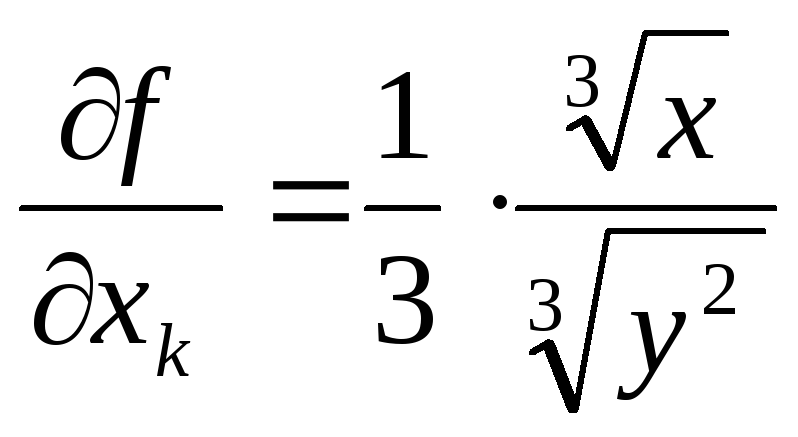 и ясно, что эти производные терпят разрыв
в точке
и ясно, что эти производные терпят разрыв
в точке
![]() .
Но приращение
.
Но приращение
![]() не имеет вид
не имеет вид
![]() ,
где
,
где
![]() при
при
![]() .Действительно,
полагая
.Действительно,
полагая
![]() и
предполагая, что
и
предполагая, что
![]() получаем
получаем
![]() ,
или
,
или
![]() что
невозможно, так как при
что
невозможно, так как при
![]() правая часть стремится к 0, а левая нет!
правая часть стремится к 0, а левая нет!
