
- •Основные теоремы о пределах.
- •Непрерывность функции в точке и на интервале.
- •Непрерывность функции в точке.
- •Производная и дифференциал.
- •Поиск экстремума функции двух переменных.
- •Определенный интеграл, основные теоремы.
- •Понятие о дифференциальном уравнении: его порядке, общем и частном решении.
- •Дифференциальные уравнения первого порядка: с разделяющимися переменными.
- •Линейные дифференциальные уравнения, однородные и неоднородные. Понятие общего решения линейного уравнения.
- •Числовой ряд. Сходимость и сумма ряда. Признак Даламбера.
- •Признаки сходимости
Графики и свойства основных элементарных функций.
К
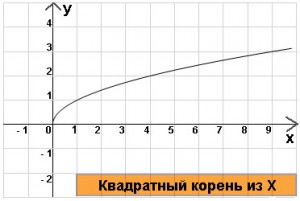 вадратный
корень, функция
вадратный
корень, функция
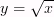 Свойства:
1)
Область определения:
Свойства:
1)
Область определения:
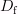 =
[
=
[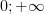 )
2)
Область значений:
)
2)
Область значений:
 =
[
)
3)
Промежуток возрастания:
[
)
4)
Промежутки убывания: нет
5)
Нули функции:
=
[
)
3)
Промежуток возрастания:
[
)
4)
Промежутки убывания: нет
5)
Нули функции:
 6)
Промежутки знакопостоянства:
y>0
если
6)
Промежутки знакопостоянства:
y>0
если
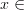 (
)
y<0,
нет таких Х
(
)
y<0,
нет таких Х
 Показательная
функция
Показательная
функция
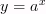 ,
где a > 1
Свойства:
1)
Область определения:
=
(
,
где a > 1
Свойства:
1)
Область определения:
=
( )
2)
Область значений:
=
(
)
3)
Промежуток возрастания:
(
)
4)
Промежутки убывания: нет
5)
Нули функции: нет
6)
Промежутки знакопостоянства:
y>0
если
(
)
y<0,
нет таких Х
)
2)
Область значений:
=
(
)
3)
Промежуток возрастания:
(
)
4)
Промежутки убывания: нет
5)
Нули функции: нет
6)
Промежутки знакопостоянства:
y>0
если
(
)
y<0,
нет таких Х
П
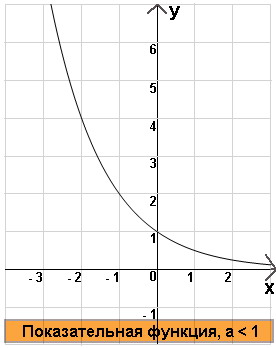 оказательная
функция
,
где a < 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=
(
)
3)
Промежутки возрастания: нет
4)
Промежуток убывания:
(
)
5)
Нули функции: нет
6)
Промежутки знакопостоянства:
y>0
если
(
)
y<0,
нет таких Х
оказательная
функция
,
где a < 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=
(
)
3)
Промежутки возрастания: нет
4)
Промежуток убывания:
(
)
5)
Нули функции: нет
6)
Промежутки знакопостоянства:
y>0
если
(
)
y<0,
нет таких Х
Л
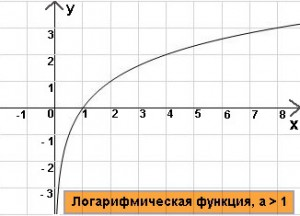 огарифмическая
функция
огарифмическая
функция
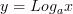 ,
a > 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=
(
)
3)
Промежуток возрастания: (
)
4)
Промежуток убывания: нет
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:
y>0
если
(
,
a > 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=
(
)
3)
Промежуток возрастания: (
)
4)
Промежуток убывания: нет
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:
y>0
если
(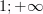 )
y<0
если
(
)
y<0
если
(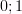 )
)Логарифмическая функция , a < 1 Свойства: 1
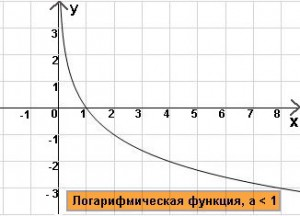 )
Область определения:
=
(
)
2)
Область значений:
=(
)
3)
Промежуток возрастания: нет
4)
Промежуток убывания:(
)
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:
y>0
если
(
)
y<0
если
(
)
)
Область определения:
=
(
)
2)
Область значений:
=(
)
3)
Промежуток возрастания: нет
4)
Промежуток убывания:(
)
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:
y>0
если
(
)
y<0
если
(
)Т
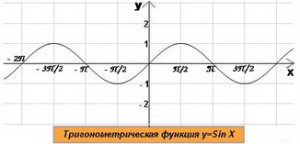 ригонометрическая
функция
ригонометрическая
функция
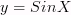 Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[
Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[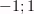 ]
3)
Промежутки возрастания: [
]
3)
Промежутки возрастания: [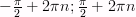 ],
где
],
где
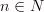 4)
Промежутки убывания: [
4)
Промежутки убывания: [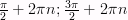 ],
где
5)
Нули функции:
],
где
5)
Нули функции:
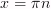 ,
где
6)
Промежутки знакопостоянства:
y>0
если
[
,
где
6)
Промежутки знакопостоянства:
y>0
если
[
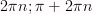 ],
где
y<0
если
[
],
где
y<0
если
[
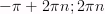 ],
где
],
где
Т
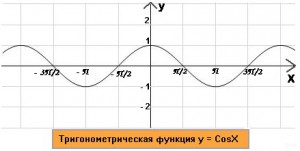 ригонометрическая
функция
ригонометрическая
функция
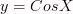 Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[
]
3)
Промежутки возрастания: [
],
где
4)
Промежутки убывания: [
],
где
5)
Нули функции:
Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[
]
3)
Промежутки возрастания: [
],
где
4)
Промежутки убывания: [
],
где
5)
Нули функции:
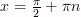 ,
где
6)
Промежутки знакопостоянства:
y>0
если
[
,
где
6)
Промежутки знакопостоянства:
y>0
если
[
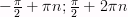 ],
где
y<0
если
[
],
где
],
где
y<0
если
[
],
где
Предел функции
Предел функции. Число L называется пределом функции y = f ( x ) при x, стремящемся к a :
![]()
если для любого
![]() >
0 найдётся такое положительное
число
>
0 найдётся такое положительное
число
![]() =
(
),
зависящее от
,
что из условия | x
a | <
следует
| f ( x ) – L | <
=
(
),
зависящее от
,
что из условия | x
a | <
следует
| f ( x ) – L | <
Это определение означает, что L есть предел функции y = f ( x ), если значение функции неограниченно приближается к L , когда значение аргумента x приближается к a. Геометрически это значит, что для любого > 0 можно найти такое число , что если x находится в интервале ( a a ), то значение функции лежит в интервале ( L , L + ). Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.
Основные теоремы о пределах.
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
![]() Þ
Þ
![]()
![]() .
.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
![]() Þ
Þ
![]() .
.
Теорема 3. Предел постоянной равен самой постоянной.
![]() .
.
Доказательство. f(x)=с,
докажем, что
![]() .
.
Возьмем произвольное e>0. В качестве d можно взять любое
положительное число. Тогда при
![]()
![]() .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
![]() и
и
![]() .
.
По теореме о связи предела и бесконечно малой функции:
f(x)-A=![]() - б.м. при
- б.м. при
![]() ,
,
f(x)-B=![]() - б.м. при
.
- б.м. при
.
Вычитая эти равенства, получим:![]()
B-A= - .
Переходя к пределам в обеих частях равенства при , имеем:
B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.
Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при , то и алгебраическая сумма имеет предел при , причем предел алгебраической суммы равен алгебраической сумме пределов.
![]()
![]()
![]()
![]() .
.
Доказательство. Пусть
,
![]() ,
,
![]() .
.
Тогда, по теореме о связи предела и б.м. функции:
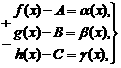 где
где
![]() - б.м. при
.
- б.м. при
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)=![]() ,
,
где
![]() б.м.
при
.
б.м.
при
.
По теореме о связи предела и б.м. функции:
![]() А+В-С=
А+В-С=
![]() .
.
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при , то и произведение имеет предел при , причем предел произведения равен произведению пределов.
![]()
![]()
![]() .
.
Следствие. Постоянный множитель можно выносить за знак предела.
![]()
![]()
![]() .
.
Теорема 7. Если функции f(x) и g(x) имеют предел при ,
причем
![]() ,
то и их частное имеет предел при
,
причем предел частного равен частному
пределов.
,
то и их частное имеет предел при
,
причем предел частного равен частному
пределов.
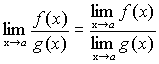 ,
.
,
.
Непрерывность функции в точке и на интервале.
Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
![]()
Тот же факт можно записать иначе:
![]()
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию
![]()
верно неравенство
![]() .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
