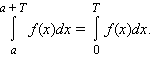16. Определенный интеграл, основные теоремы.

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

Пусть определена на . Разобьём на части с несколькими произвольными точками Тогда говорят, что произведено разбиение отрезка Далее выберем произв. точку , , Определённым интегралом от функции на отрезке называется предел интегральных сумм при , если он существует независимо от разбиения и выбора точек , т.е. 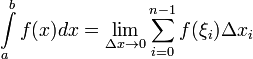(1) Если существует (1), то функция называется интегрируемой на – определение интеграла по Риману.

• 

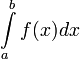
• – нижний предел.

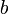• – верхний предел.

• – подынтегральная функция.

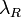• - длина частичного отрезка.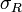

• – интегральная сумма от функции на соответствующей разбиению .

• - максимальная длина част. отрезка.

Определение интеграла на языке , :(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λ_R < δ, выполняется неравенство: |I- σ_R | = |∑^n-1_i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫_a^bf(x)dx

свойства Если функция интегрируема на [a; b], то она интегрируема на любом отрезке

• Для любых a, b и c

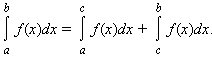
• Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A

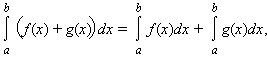
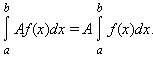
• Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.

• Если f (x) – периодическая функция с периодом T, то для любого a

17. Понятие о дифференциальном уравнении: его порядке, общем и частном решении.

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.