11. Поиск экстремума функции двух переменных.

Пусть функция определена в некоторой области G и точка .

Функция имеет в точке максимум, если существует такая окрестность этой точки, что для всех точек этой окрестности, отличных от , выполняется неравенство .

Аналогично определяется минимум функции.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума). Если –точка экстремума функции , то частные производные и в этой точке равны нулю или не существуют.

Точки, в которых частные производные и обращаются в нуль или не существуют, называются критическими точками этой функции.

Сформулированный признак не является достаточным: не обязательно критическая точка является точкой экстремума.

Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума).

Пусть в некоторой области, содержащей точку , функция имеет непрерывные частные производные до 3–го порядка включительно и . Обозначим: . Тогда

1)если , то функция имеет экстремум в точке , причем это максимум, если и минимум, если ;

2)если , то экстремума в точке нет;

3)если , требуется дополнительное исследование (экстремум в точке может быть или не быть).

12. Неопределенный интеграл. Основные теоремы ( не могу найти).

Неопределённый интегра́л для функции  — это совокупность всех первообразных данной функции.

Если функция определена и непрерывна на промежутке и  — её первообразная, то есть при , то

,

где С — произвольная постоянная.

Если , то и , где  — произвольная функция, имеющая непрерывную производную

13. Интегрирование подстановкой.

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл Сделаем подстановку где  — функция, имеющая непрерывную производную.

Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

14. Интегрирование по частям.

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

для определённого:

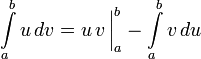
15. Интегрирование рациональной функции.

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь , знаменатель которой разложен на множители

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

где  — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.