
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
Вопрос 15: символы ,. Вычисление ,,
Пусть
![]() ,
,![]() определены в
определены в![]() .
.
Определение
15.1.
![]() ,
,![]() ,
если существует
,
если существует![]() ,
,![]() – б. м. при
– б. м. при![]() такая, что
такая, что![]() .
.
Определение
15.2.
![]() ,
,![]() ,
если существует
,
если существует![]() ,
– ограниченная в
,
– ограниченная в![]() ,
такая, что
,
такая, что![]() .
.
Примеры.
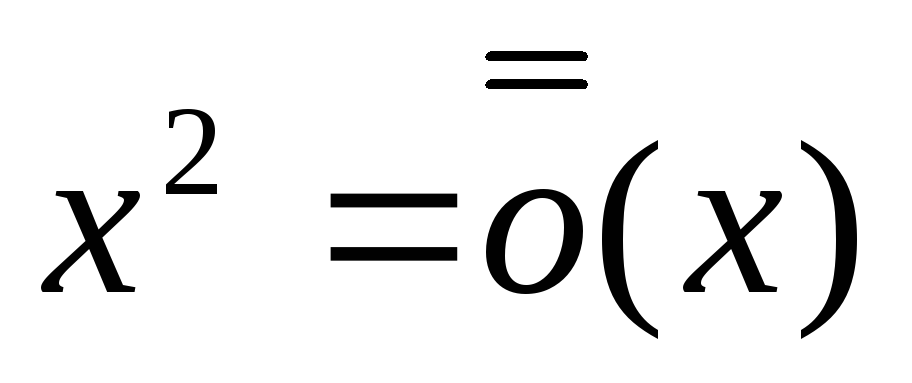 при
при
 ,
т.к.
,
т.к.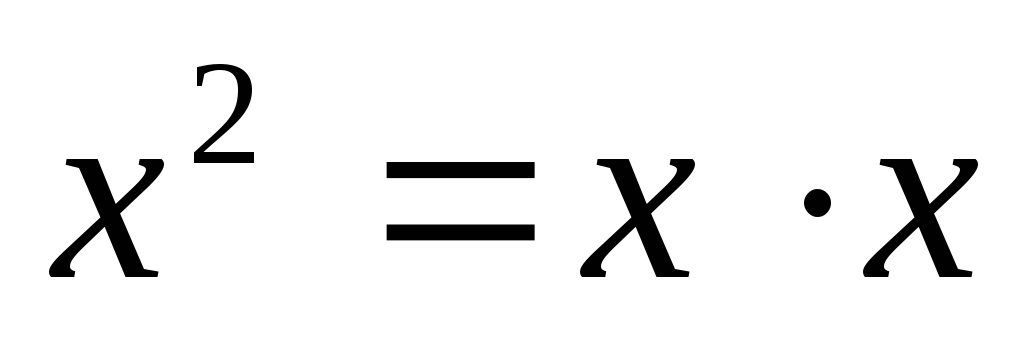 ,
а
,
а ;но
;но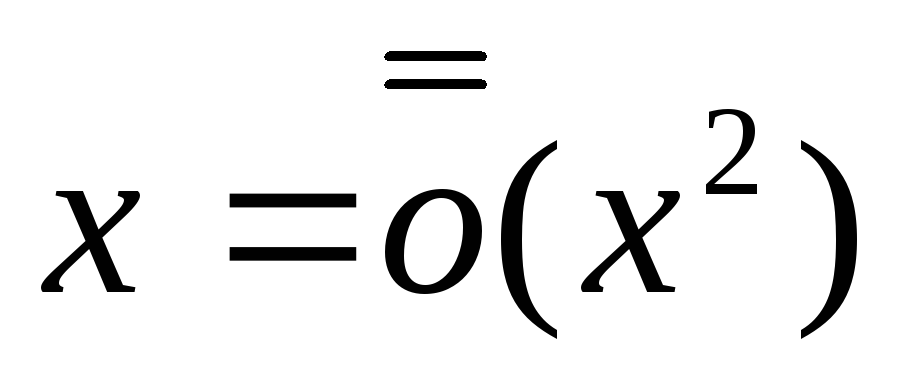 ,
при
,
при
 ∞,
т.к.
∞,
т.к.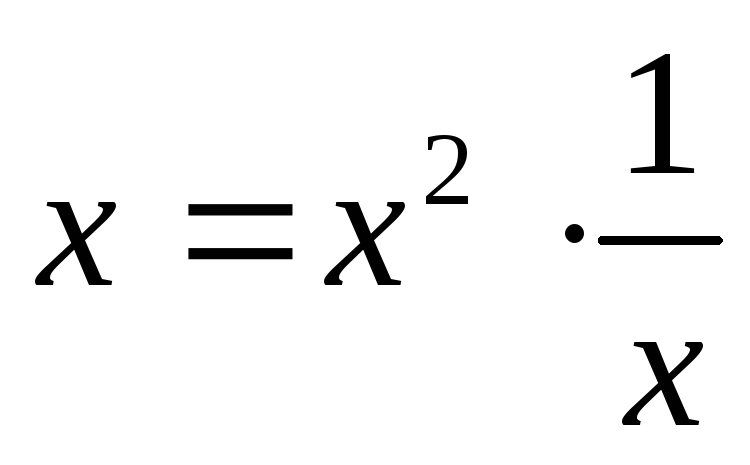 ,
и
,
и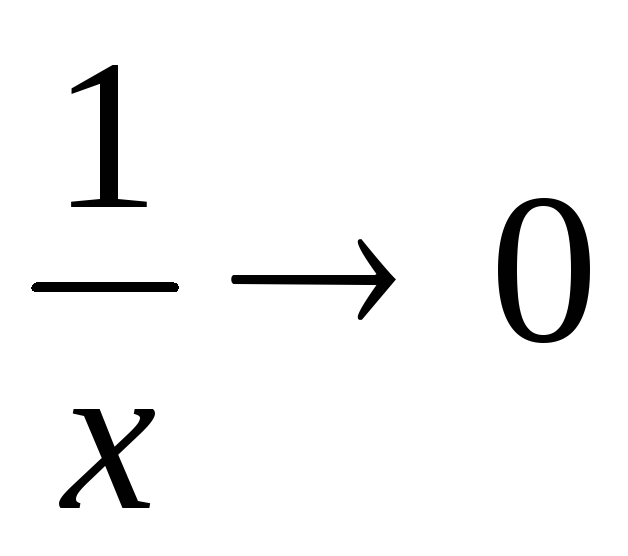 при
при ∞.
∞.
Вообще,
если
![]() и
и![]() ,
то
,
то![]() и если
и если![]() и
и![]() ∞
то
∞
то![]() .
.
Из
свойств бесконечно малых величин следуют
такие свойства символов
![]() ,
,
![]() :
:
Теорема
15.1.Если
![]() ,
,![]() ,
то
,
то![]() ,
,![]() ;
все соотношения выписаны при
;
все соотношения выписаны при![]() .
.
Доказательство.
Действительно,
![]() ,
,![]() ,
,![]() – б. м. при
– б. м. при![]() и
и![]() ,
а
,
а![]() .В
фигурных скобках стоят бесконечно малые
при
.В
фигурных скобках стоят бесконечно малые
при![]() .
.
Теорема
15.2.![]() ,
т.е.
,
т.е.
если
![]() ,
то
,
то![]() при
при![]() .
.
Доказательство.
Действительно, если
![]() ,
а
,
а![]() ,
т. е.
,
т. е.![]() ,
,![]() ,
где
,
где![]() ,
,![]() – б. м. при
– б. м. при![]() ,
то
,
то![]() ,
где
,
где![]() – б. м. при
– б. м. при![]() ,
что и означает справедливость
доказываемого равенства . Для большей
ясности повторим, что равенство следует
понимать так: если
,
что и означает справедливость
доказываемого равенства . Для большей
ясности повторим, что равенство следует
понимать так: если![]() ,
то
,
то![]() при
при![]() .
.
Теорема
15.3.![]() ,
,![]() ,
,![]()
Доказательство.Эти свойства сразу следуют из того, что произведение бесконечно малой величины на ограниченную есть бесконечно малая величина.
Символы
![]() ,
,![]() удобны при вычислении пределов.
удобны при вычислении пределов.
Перейдём
к вычислению пределов
![]() ,
,![]() ,
,![]() ,
которые далее будут использованы при
вычислении производных.
Вновь
подчеркнём, что при ответе на этот билет
при их вычислении нельзя пользоваться
правилами Лопиталя или формулой Тейлора.
Разумеется, они дадут верный ответ, но
их применение требует знания производных
функций, стоящих в числителях этих
дробей. А для вычисления этих производных,
как отмечено выше, требуется знать эти
самые пределы. Поэтому получится не
доказательство, а порочный логический
круг.
,
которые далее будут использованы при
вычислении производных.
Вновь
подчеркнём, что при ответе на этот билет
при их вычислении нельзя пользоваться
правилами Лопиталя или формулой Тейлора.
Разумеется, они дадут верный ответ, но
их применение требует знания производных
функций, стоящих в числителях этих
дробей. А для вычисления этих производных,
как отмечено выше, требуется знать эти
самые пределы. Поэтому получится не
доказательство, а порочный логический
круг.
Теорема
15.4.
![]() =1,
=1,![]() =
=![]() ,
,![]() =
=![]() .
.
Доказательство.
1.
В теореме 11.2 мы установили, что
![]() .
Рассмотрим левую часть этого равенства
и преобразуем её так:
.
Рассмотрим левую часть этого равенства
и преобразуем её так:![]() .
По непрерывности показательной функции
(а именно: непрерывность функции означает,
что
.
По непрерывности показательной функции
(а именно: непрерывность функции означает,
что
![]() )
получаем
)
получаем
![]() ,
т. е.
,
т. е.![]()
2.Далее
рассмотрим предел
![]() и сделаем в нём замену переменной
и сделаем в нём замену переменной![]() (это – монотонная замена и теорема о
пределе сложной функции будет верна).
При
(это – монотонная замена и теорема о
пределе сложной функции будет верна).
При![]() и
и![]() ,
и наоборот, при
,
и наоборот, при![]() также
также![]() .
.
Поэтому
![]() ,
по доказанному выше.
,
по доказанному выше.
Для
![]() имеем
имеем![]()
3.
Рассмотрим
![]() .
Обозначим
.
Обозначим![]() ,
т. е.
,
т. е.![]() .
Тогда
.
Тогда
![]() ,
,![]() и
при
и
при![]() переменная
переменная![]() ,
и наоборот, при
,
и наоборот, при![]() переменная
переменная![]() .
Наш
предел примет вид
.
Наш
предел примет вид![]() .
Это преобразование законное, т. к. при
.
Это преобразование законное, т. к. при![]() и
и![]() ,
поэтому
,
поэтому![]() .
Далее используем доказанное в первом
пункте равенство. Таким образом, искомый
предел равен
.
Далее используем доказанное в первом
пункте равенство. Таким образом, искомый
предел равен![]() .
.
Запишем
найденные предельные соотношения с
помощью символа
![]() .
.
![]() означает,
что
означает,
что
![]() ,
,![]() при
при
![]() или,
или,
![]() ,
,
![]() .
.
Равенство
![]() означает, что
означает, что![]() ,
,![]() .
.
Аналогично,
![]() ,
,![]() .
.
(Кстати,
![]() означает, что
означает, что
![]() при
при
![]() ).
).
Вопрос 16: промежуточные значения непрерывной на отрезке функции
Определение
16.1. Пусть
функция
![]() определена на некотором множестве
определена на некотором множестве![]() .
Если она непрерывна в каждой точке
этого множества, то говорят, что онанепрерывна
на множестве
.
Если она непрерывна в каждой точке
этого множества, то говорят, что онанепрерывна
на множестве
![]() .Иными
словами, функция
.Иными
словами, функция![]() непрерывна на множестве
непрерывна на множестве![]() ,
если для любого числа
,
если для любого числа![]() и любого
и любого![]() существует
такое число
существует
такое число![]() ,
что для всех
,
что для всех![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству![]() выполняется
неравенство
выполняется
неравенство![]() .
.
Теорема
16.1.(Больцано, Коши) Пусть
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке![]() и принимает на его концах значения
разных знаков. Тогда существует хотя
бы одна точка
и принимает на его концах значения
разных знаков. Тогда существует хотя
бы одна точка![]() такая, что
такая, что![]() .
.
Пусть,
для определённости,
![]() .
Обозначим
.
Обозначим![]() и рассмотрим точку
и рассмотрим точку![]() .
Если оказалось, что
.
Если оказалось, что![]() ,
то теорема верна при
,
то теорема верна при![]() .
Если же
.
Если же![]() ,
то либо
,
то либо![]() и в этом случае положим
и в этом случае положим![]() ,
либо
,
либо![]() и в этом случае положим
и в этом случае положим![]() .
В обоих случаях получен отрезок
.
В обоих случаях получен отрезок![]() ,
длина которого равна половине длины
отрезка
,
длина которого равна половине длины
отрезка![]() и на концах которого функция
и на концах которого функция
![]() принимает значения разных знаков.
принимает значения разных знаков.
Разделим
этот отрезок пополам точкой
![]() .
Если
.
Если![]() ,
то теорема верна при
,
то теорема верна при![]() .
Если же
.
Если же![]() ,
то либо
,
то либо![]() и в этом случае положим
и в этом случае положим![]() ,
либо
,
либо![]() и в этом случае положим
и в этом случае положим![]() .
Снова обоих случаях получен отрезок
.
Снова обоих случаях получен отрезок![]() ,
длина которого равна половине длины
отрезка
,
длина которого равна половине длины
отрезка![]() и на концах которого функция
и на концах которого функция
![]() принимает значения разных знаков.
принимает значения разных знаков.
Продолжим
процесс деления отрезков пополам. При
этом возникают две возможности. Либо
на каком- то шаге получаем, для
![]() ,
и
,
и![]() .
Тогда теорема справедлива. Либо для
всех
.
Тогда теорема справедлива. Либо для
всех![]() выполняются неравенства
выполняются неравенства![]() .
Тогда получается бесконечная система
стягивающихся отрезков. Действительно,
по построению каждый следующий отрезок
вложен в предыдущий, а длина отрезка
.
Тогда получается бесконечная система
стягивающихся отрезков. Действительно,
по построению каждый следующий отрезок
вложен в предыдущий, а длина отрезка![]() ,
равная
,
равная![]() ,
стремится к нулю при
,
стремится к нулю при![]() .
Эти отрезки имеют общую точку, которую
будем обозначать
.
Эти отрезки имеют общую точку, которую
будем обозначать![]() .
Докажем, что
.
Докажем, что
![]() .
.
Действительно,
с одной стороны,
![]() ,
поэтому, по теореме о предельном переходе
в неравенствах,
,
поэтому, по теореме о предельном переходе
в неравенствах,![]() ,
так как функция
,
так как функция![]() по условию непрерывна на отрезке
по условию непрерывна на отрезке![]() и
и![]() .
С другой стороны,
.
С другой стороны,![]() ,
так как
,
так как![]() .
Полученные неравенства доказывают, что
.
Полученные неравенства доказывают, что
![]() .
.
Следствие.
Пусть
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке![]() ,
,![]() и пусть
и пусть![]() (
(![]() ).
Тогда для любого числа
).
Тогда для любого числа
![]() ,
удовлетворяющего неравенствам
,
удовлетворяющего неравенствам![]() (
(![]() ),
существует точка
),
существует точка
![]() такая, что
такая, что![]() .
.
Рассмотрим
функцию
![]() .
Она непрерывна на отрезке
.
Она непрерывна на отрезке![]() как разность непрерывной по условию
функции
как разность непрерывной по условию
функции
![]() и
постоянной функции.
и
постоянной функции.
![]() ,
поэтому существует точка
,
поэтому существует точка![]() такая, что
такая, что![]() ,
т.е.
,
т.е.![]() .
.
