
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
4. Правила дифференцирования
Дифференцирование
линейной комбинации, произведения и
частного.
Теорема
19.5
Пусть
![]() имеет
производную в точке
имеет
производную в точке
![]() .
Тогда для любой постоянной
.
Тогда для любой постоянной
![]() справедлива
формула:
справедлива
формула:
![]()
(постоянный
множитель можно вынести за знак
производной).
◄Приращение
функции
![]() в точке
в точке![]() равно
равно
![]() .
Поскольку
существует
.
Поскольку
существует
![]() , существует и
, существует и
![]() что и требовалось доказать.►
что и требовалось доказать.►
Теорема
19.6
Пусть
![]() и
и
![]() имеют
производные в точке
имеют
производные в точке
![]() .Тогда
существует производная сумма этих
функций, причём
.Тогда
существует производная сумма этих
функций, причём
![]() .
.
◄
Приращение
функции
![]() в точке
в точке![]() равно
равно
![]() ,
,
поэтому
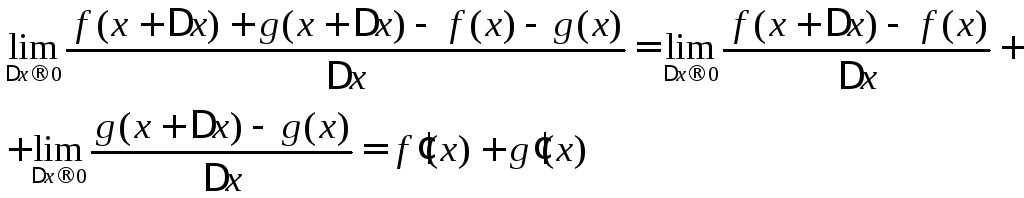
►
Напомним,
что линейной комбинацией функций![]() называют
всякую функцию
называют
всякую функцию
![]() ,
представимую в виде
,
представимую в виде
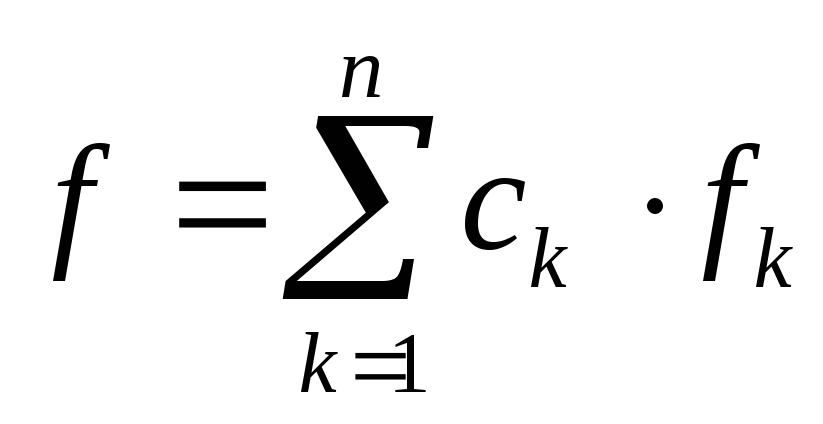 ,
где коэффициенты
,
где коэффициенты
![]() -
постоянные. Областью ее определения
служит пересечение областей определения
функций
-
постоянные. Областью ее определения
служит пересечение областей определения
функций
![]() .
Из теорем 19.5 и 19.6 следует
.
Из теорем 19.5 и 19.6 следует
Теорема
19.7
(линейное
свойство операции дифференцирования).
Если
функции
![]() дифференцируемы
в точке
дифференцируемы
в точке
![]() ,
то всякая линейная комбинация
,
то всякая линейная комбинация
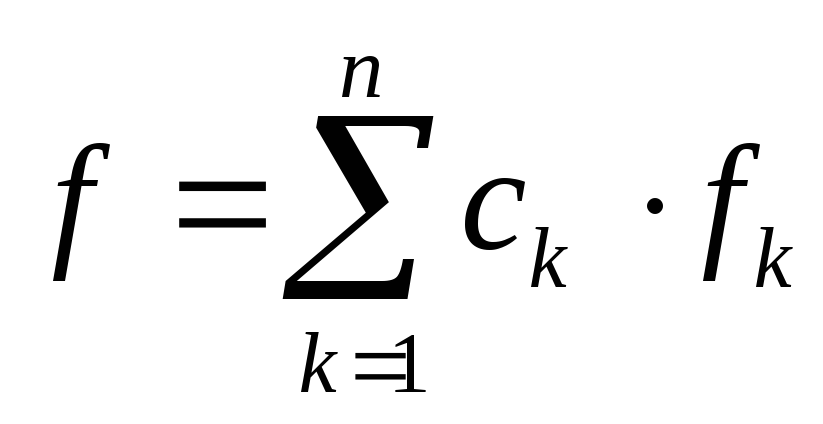 этих
функций дифференцируема в точке
этих
функций дифференцируема в точке
![]() ,
причем
,
причем
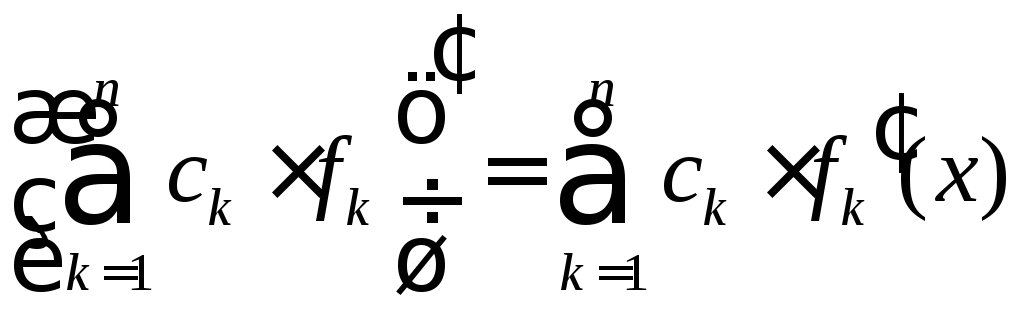 .
.
Теорема
19.8 Если
функции![]() и
и
![]() дифференцируемы в точке
дифференцируемы в точке![]() ,
то их произведение
,
то их произведение
![]()
![]() дифференцируемо в точке
дифференцируемо в точке
![]() ,
причем
,
причем
![]() .
.
◄Приращение
произведения
![]()
![]() равно
равно
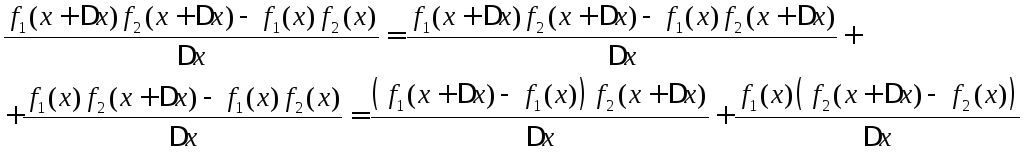
При
![]() выполняются
соотношения
выполняются
соотношения
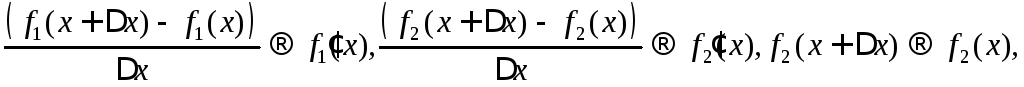
откуда, по теореме 8.4 , получаем утверждение теоремы. ►
Теорема
19.9. Если
функции
![]() и
и
![]() дифференцируемы в точке
дифференцируемы в точке![]() ,
и
,
и
![]() то
их частное
то
их частное
![]() дифференцируемо
в точке
дифференцируемо
в точке
![]() ,
причем
,
причем
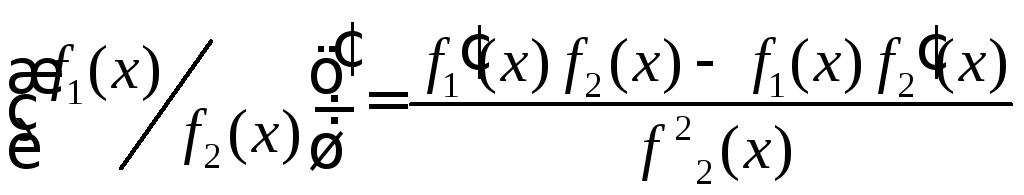 .
.
◄ Сначала докажем лемму
Лемма
19.1.
Если функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
и
,
и
![]() то
функция
то
функция
![]() дифференцируема
в точке
дифференцируема
в точке
![]() ,
причем
,
причем
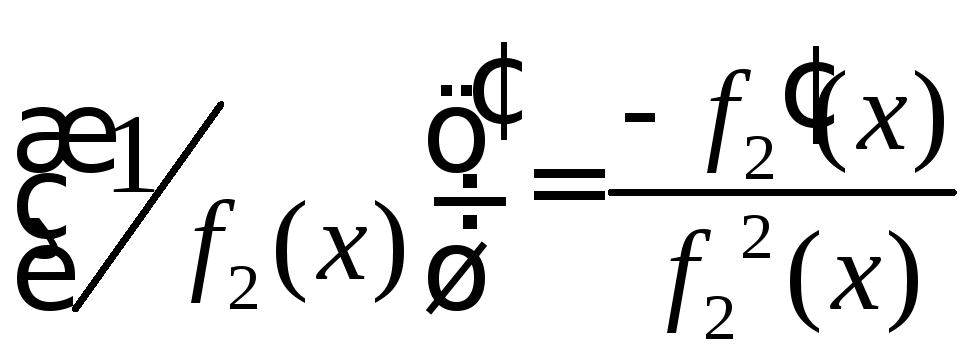 .
.
◄Приращение имеет вид:
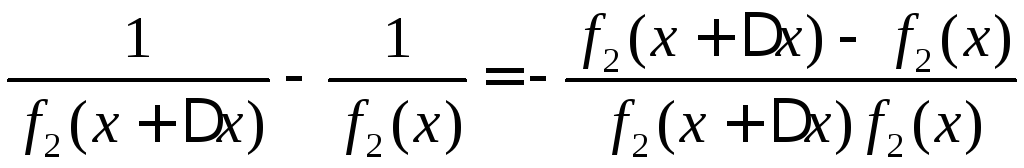
По
лемме 8.2 функция![]() определена
в окрестности точки
определена
в окрестности точки
![]() и по лемме 8.3 .
Следовательно,
и по лемме 8.3 .
Следовательно,
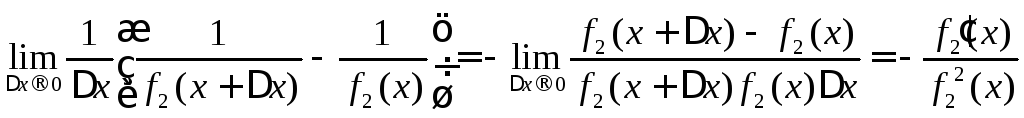 .►
.►
Теорема 19.9 сразу следует из теоремы 19.8 и леммы 19.1.
Предельные величины.
Пусть
![]() обозначает
величину издержек производства,
рассматриваемую, как функцию от количества
обозначает
величину издержек производства,
рассматриваемую, как функцию от количества
![]() выпускаемой продукции. Если
выпускаемой продукции. Если
![]() прирост
продукции,
прирост
продукции,
![]() приращение издержек производства , то
приращение издержек производства , то![]() среднее приращение издержек производства
на единицу продукции. Производная
среднее приращение издержек производства
на единицу продукции. Производная![]() выражаетпредельные
издержки производства
и является приблизительной характеристикой
дополнительных затрат на производство
единицы дополнительной продукции.
выражаетпредельные
издержки производства
и является приблизительной характеристикой
дополнительных затрат на производство
единицы дополнительной продукции.
Вполне аналогично определяются предельная выручка, предельный доход, предельная полезность и т.п.
Предельные величины также часто называют маржинальными .
Вопрос :ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ, ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ, ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ, ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
Этот вопрос является дополнительным к вопросу 19. Хотя он не включён в билеты, информацию, в нём содержащуюся, знать на экзамене обязательно!
1.Производная
степенной функции
![]() ,
где
,
где
![]() − любое вещественное число). Область
определения этой функции зависит от
− любое вещественное число). Область
определения этой функции зависит от![]() .
Имеем (при
.
Имеем (при![]() )
)
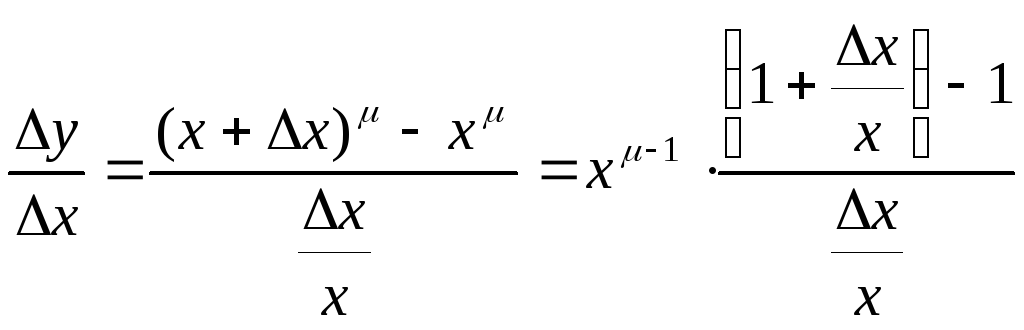 .
.
Если воспользоваться пределом, вычисленным в теореме 15.4, то получим
![]() .
.
В частности
если
![]() ,
то
,
то![]()
если
![]() ,
то
,
то![]() .
.
2.Производная
показательной функции
![]() (
(![]() ,
,![]() ).
Здесь
).
Здесь
![]() .
.
Воспользовавшись пределом, вычисленным в теореме 15.4, найдём:
![]() .
.
В частности,
если
![]() ,
то и
,
то и![]() .
.
Итак,
скорость возрастания показательной
функции ( при
![]() )
пропорциональна значению самой функции:
чем большего значения функция уже
достигла, тем быстрее в этот момент она
растёт. Это даёт точную характеристику
роста показательной функции, о которой
мы имели уже случай говорить.
)
пропорциональна значению самой функции:
чем большего значения функция уже
достигла, тем быстрее в этот момент она
растёт. Это даёт точную характеристику
роста показательной функции, о которой
мы имели уже случай говорить.
3.
Производная логарифмической
функции
![]() (
(![]() ,
,![]() ).
В этом случае
).
В этом случае
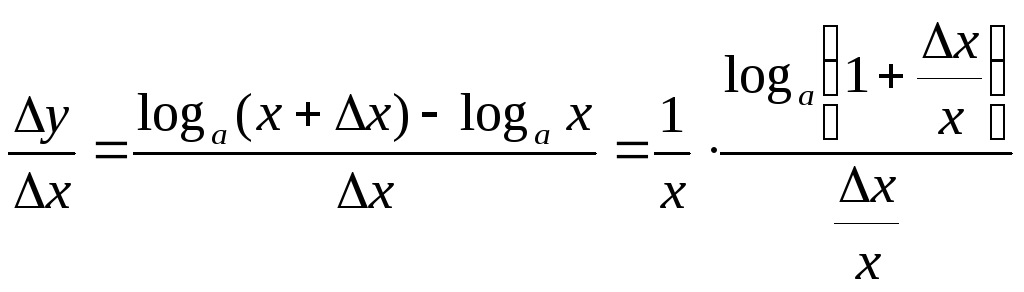 .
.
Воспользуемся пределом, вычисленным в теореме 15.4:
![]() .
.
В частности, для натурального логарифма получается исключительно простой результат:
при
![]() имеем
имеем![]() .
.
Это даёт (хотя, по существу, и не новое) основание для предпочтения, которое оказывается натуральным логарифмам при теоретических исследованиях.
4.Производные
тригонометрических функций.
Пусть
![]() ,
тогда
,
тогда
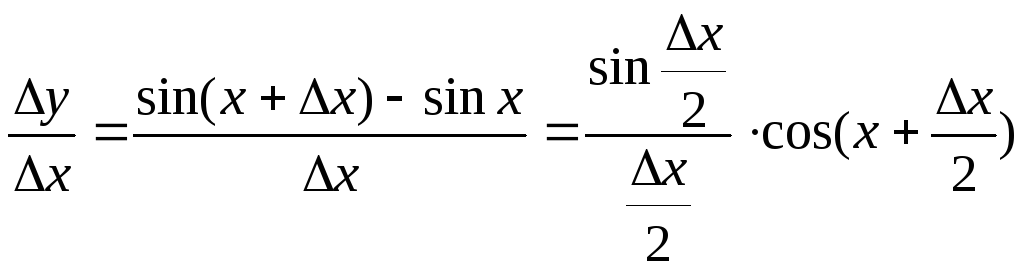 .
.
Пользуясь
непрерывностью функции
![]() и известным пределом
и известным пределом![]() ,
получим
,
получим
![]() .
.
Аналогично найдём:
если
![]() ,
то
,
то![]() .
.
В
случае
![]() применима теорема 19.9 , согласно которой
применима теорема 19.9 , согласно которой
Аналогично,
если
![]() ,
то
,
то![]() .
.
