Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций

Определение 13.1 Функция называется непрерывной в точке , если , т.е. .

Для непрерывности в точке используется обозначение.

Теорема 13.1.Если функции и непрерывны в точке , то сумма, разность, произведение и, если , то и частное этих функций - тоже непрерывны в точке .

Доказательство. Непосредственно следует из теоремы 8.4 о пределе суммы, разности, произведения и частного двух функций, имеющих пределы.

Теорема 13.2 (непрерывность сложной функции). Пустьнепрерывна в точке, причем. Пустьнепрерывна в точке . Тогда сложная функция непрерывна в точке.

◄ То, что , означает: .

То, что , означает:

Поэтому для произвольного можно сначала выбрать числотак, чтобы из неравенстваследовало неравенство. Затем по этому числунайдем число такое, что как только, так. Но тогда и, что и требовалось доказать.►

Несколько сложнее теорема о пределе сложной функции.

Теорема 13.3 Пустьопределена в проколотой окрестности точкиa, . Пустьопределена в проколотой окрестности точкиb и .

Пусть, кроме того, выполняется хотя бы одно из двух условий:

1. Непрерывна в точке ;

2. Существует такая , что.

Тогда существует и этот предел равен с.

◄Доказательство похоже на доказательство предыдущей теоремы.

То, что означает, что .

То, что означает, что .

Если потребовать, чтобы в некоторой проколотой окрестности точки a , то тогда можно по произвольному найти сначала числотакое, что если, то. Теперь по этомунаходимтак, чтобы изследовало неравенство. Пересекаем проколотые окрестности и . Это пересечение содержит некоторую проколотую окрестность точки a, и, если x принадлежит этой окрестности, то и , т.е., следовательно,. В этом случае теорема доказана. Если же ,то , поэтому выбирая по соответствующее , а потом по этому – соответствующее число получаем, что как только , так и, значит, .►

Примечание 1. Обычно при вычислении пределов мы используем монотонные замены переменной и условие 2 выполняется.

Примечание 2. Если не выполняется ни одно из условий, то может оказаться, что предел не существует, либо существует, но не равен с.

Первая ситуации встречается в таком примере:

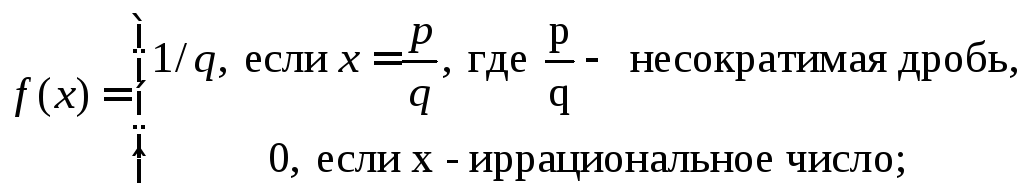
При стремлении x к 0 функция имеет пределом число 0. При стремлении y к 0 функция имеет предел, равный 1.

Однако функция

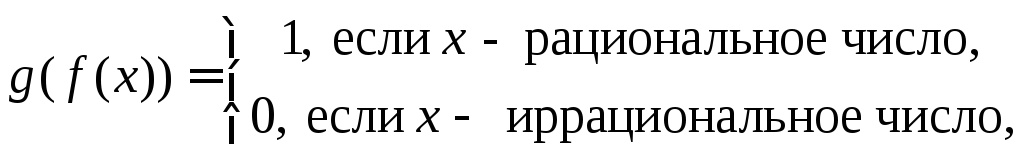
не имеет предела при .

Пример второй ситуации более простой. Пусть

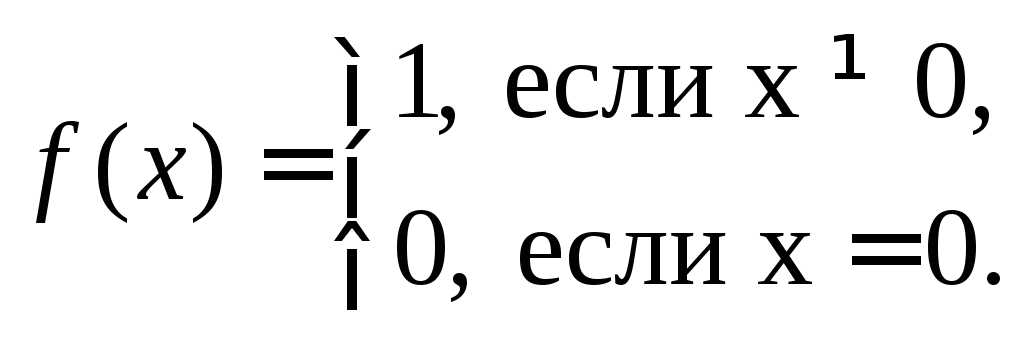
Очевидно, .

Пусть 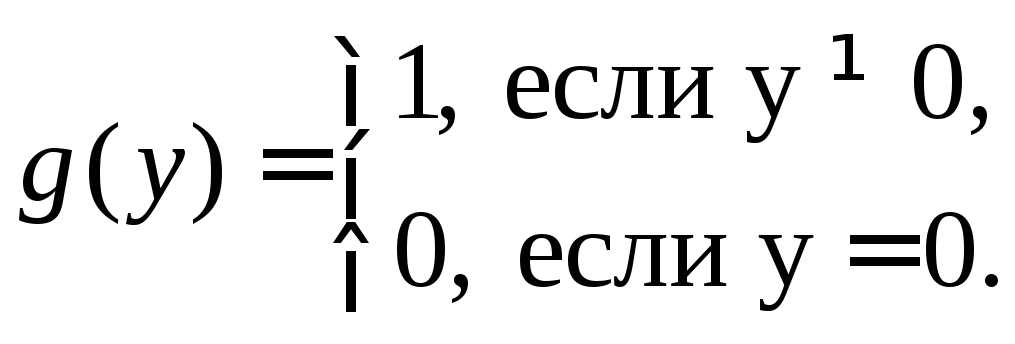. Тогда .

Однако

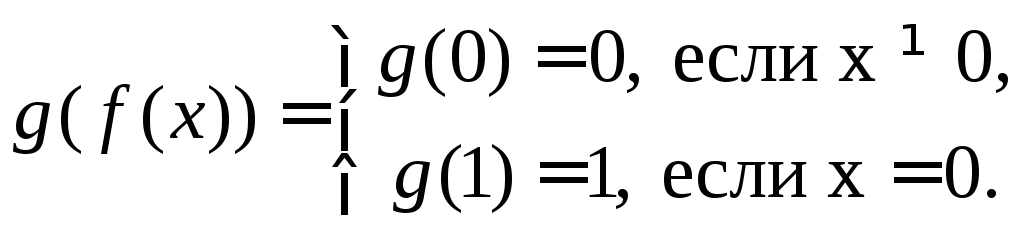
Поэтому .

Определение 13.2. Если функция не является непрерывной в точке , то говорят, что онаразрывна в этой точке.

При этом предполагаем, что либо является точкой из области определения, либо она является предельной точкой области определения.

Точки разрыва делятся на следующие классы.

Определение 13.3. Точкой устранимого разрыва называется такая точка , что существуетно при этом либо значение либоне определено, либо . В первом случае можно доопределить функцию в точке, во втором – переопределить функцию так, чтобы получилась непрерывная функция.

Поясним сказанное примерами:

1. Пусть 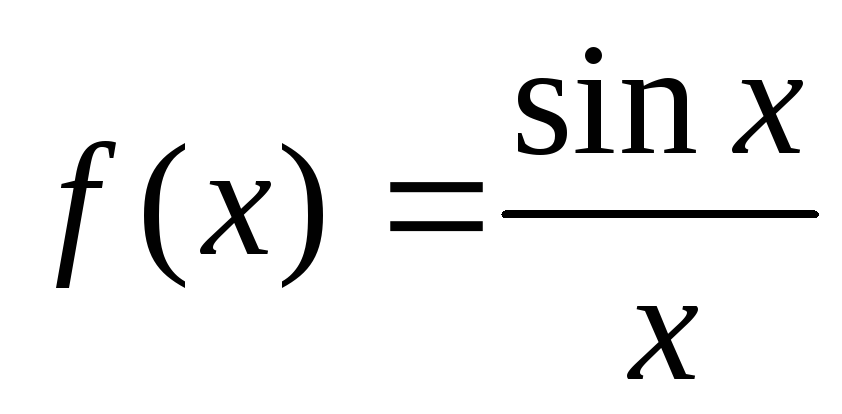. Эта функция не определена в точке 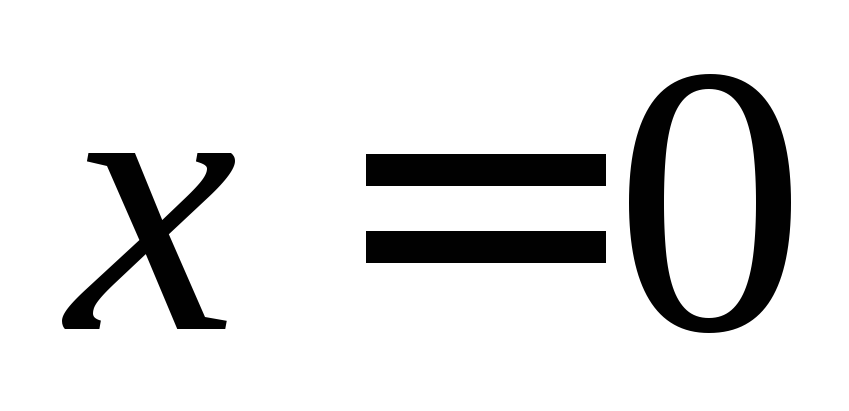,но её предел при существует и равен 1( теорема 9.5).Поэтому можно

доопределить функцию ,рассмотрев функцию

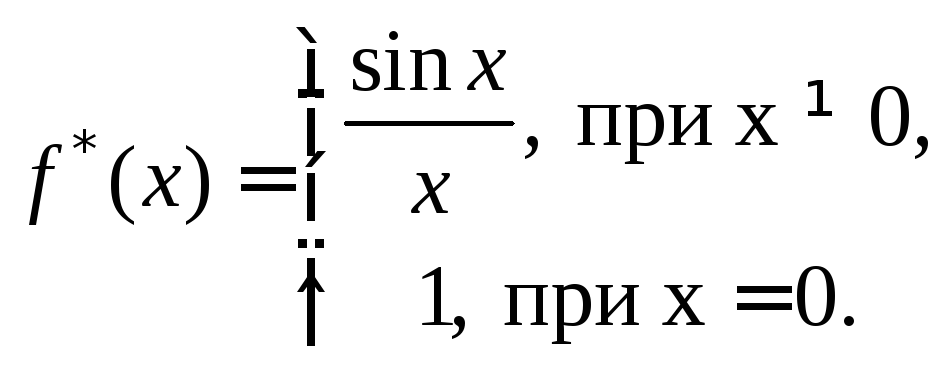
По определению, функция – непрерывна в .

2. Пусть

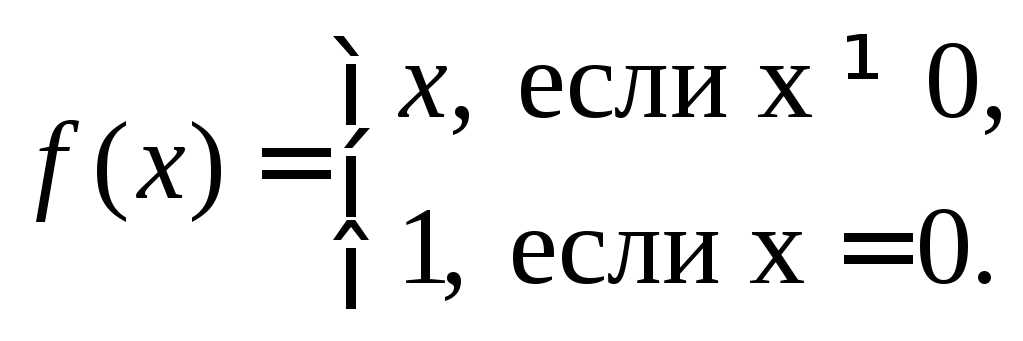
Переопределим функцию в точке, положив.

Получилась непрерывная функция .

И в том, и в другом примере разрыв удалось устранить.

Определение 13.4. Точкой разрыва первого рода называется точка,

в которой существуют и , причем.

Например, функция 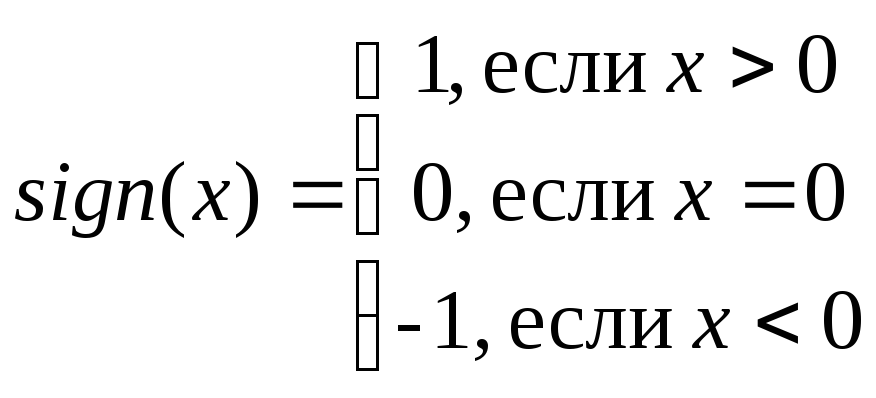обладает разрывом в точке 0 первого рода.

Замечание. По следствию теоремы 10.2 монотонная в окрестности точки функция имеет и . Поэтому она либо непрерывна в точке a, когда оба эти предела равны друг другу, либо имеет в ней разрыв первого рода, когда эти пределы различные.

Определение 13.5. Если хотя бы один из пределов , не существует, или бесконечен, то говорят, что–точка разрыва второго рода.