
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
Вопрос 12: критерий коши существования предела последовательности, предела функции
Определение
12.1.
Пусть задана последовательность
![]() и пусть
и пусть
![]() - возрастающая последовательность
натуральных чисел. Тогда последовательность
- возрастающая последовательность
натуральных чисел. Тогда последовательность
![]() подпоследовательность
исходной
последовательности.
подпоследовательность
исходной
последовательности.
Теорема
12.1.
Последовательность
![]() имеет пределA
тогда и только тогда, когда любая её
подпоследовательность имеет предел,
равный A.
имеет пределA
тогда и только тогда, когда любая её
подпоследовательность имеет предел,
равный A.
◄Поскольку
последовательность сама является одной
из своих подпоследовательностей ( для
которой
![]() ),утверждение
теоремы очевидно в одну сторону.
),утверждение
теоремы очевидно в одну сторону.
Обратно,
из определения подпоследовательности
сразу вытекает, что для любого
![]() выполняется неравенство
выполняется неравенство![]() .
Если
.
Если![]() ,то
для любого
,то
для любого![]() существует
существует![]() такое, что при
такое, что при![]() выполняется неравенство
выполняется неравенство![]() .При
этом для любой подпоследовательности
.При
этом для любой подпоследовательности![]() при
при![]() выполняется
неравенство
выполняется
неравенство![]() ,
из которого следует, что
,
из которого следует, что![]() .
Это означает, что
.
Это означает, что![]() .►
.►
Теорема 12.2. (Лемма Больцано-Вейерштрасса) Из любой ограниченной бесконечной последовательности можно извлечь подпоследовательность, сходящуюся к конечному пределу.
◄
Если множество значений , которые принимает последовательность
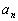 конечное, т.е.
конечное, т.е.
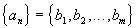 ,
то хотя бы одно из значений
,
то хотя бы одно из значений
 ,
обозначим его
,
обозначим его
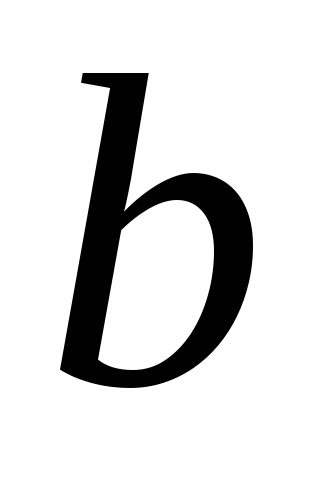 ,
она принимает бесконечно много раз,
т.е. существует бесконечное множество
номеров
,
она принимает бесконечно много раз,
т.е. существует бесконечное множество
номеров
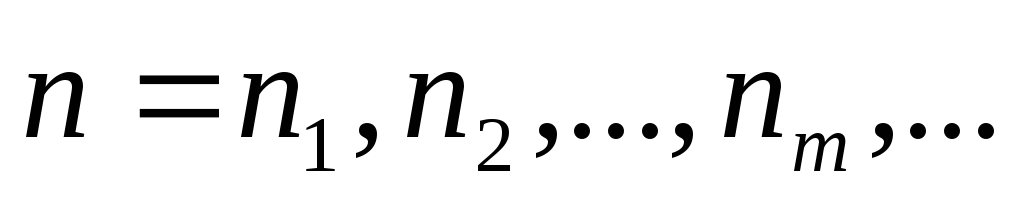 таких, что
таких, что
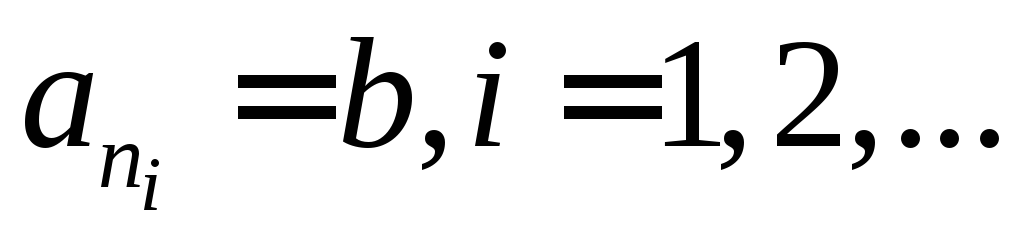 .Поэтому
.Поэтому
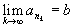 ,
подпоследовательность
,
подпоследовательность
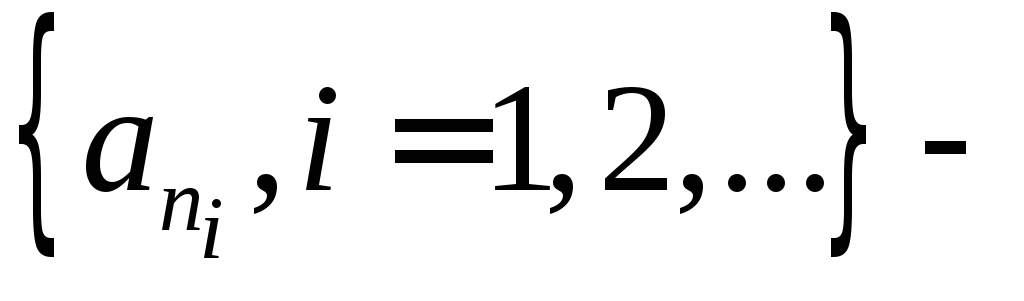 искомая.
искомая.Рассмотрим теперь случай, когда множество значений бесконечно. Так как
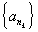 -
бесконечное ограниченное множество,
то по теореме 6.1
существует предельная точка этого
множества, равная A.
Покажем, что существует последовательность
-
бесконечное ограниченное множество,
то по теореме 6.1
существует предельная точка этого
множества, равная A.
Покажем, что существует последовательность
 такая, что
такая, что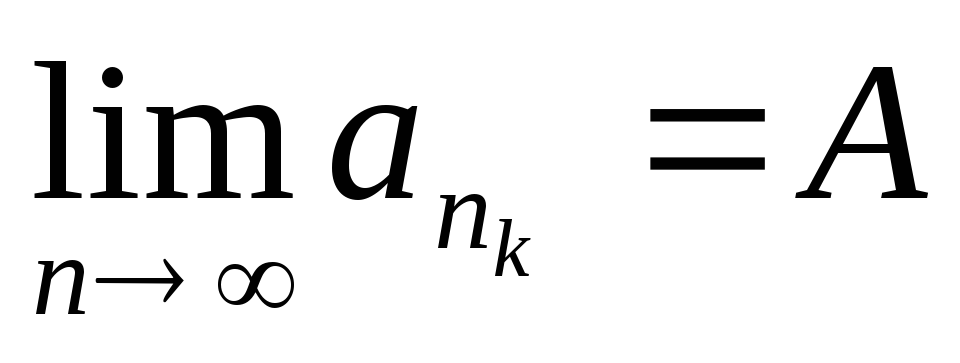 .
По определению предельной точки, для
.
По определению предельной точки, для
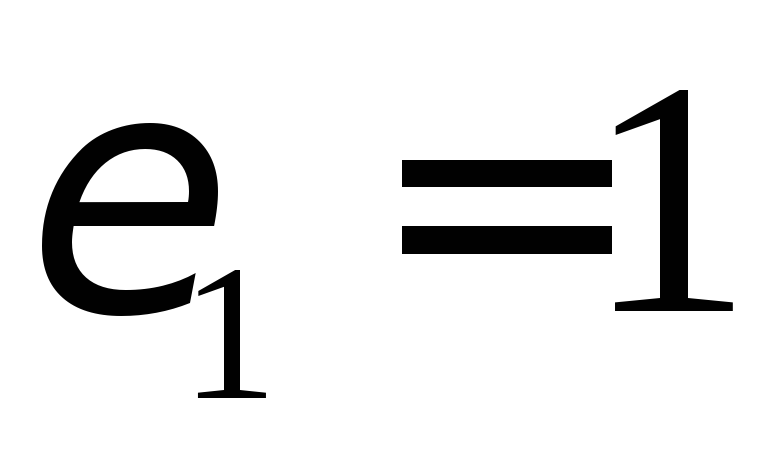 существует номер
существует номер
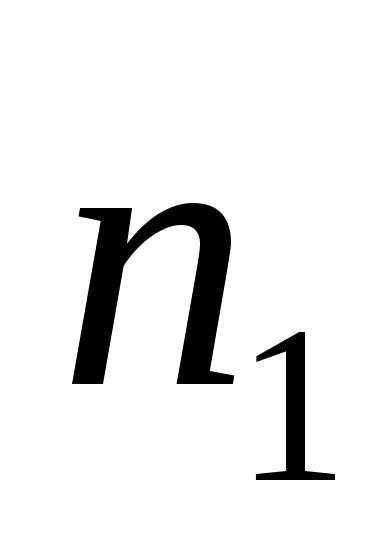 такой, что
такой, что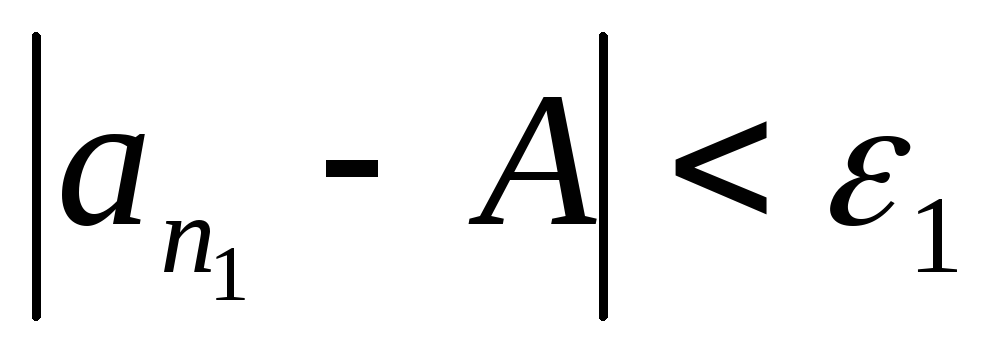 .
Положим
.
Положим
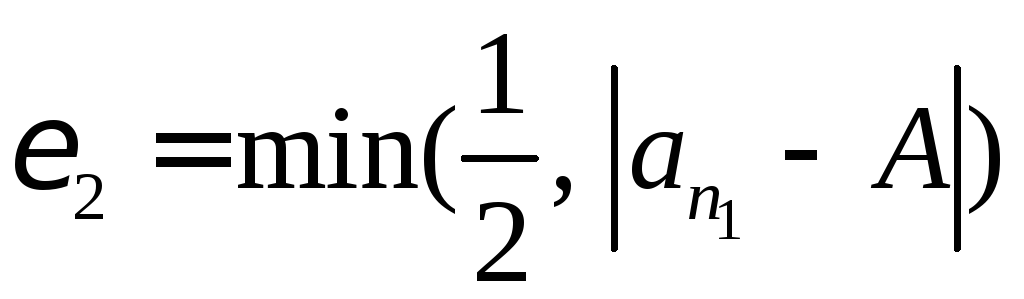 .
Существует
.
Существует
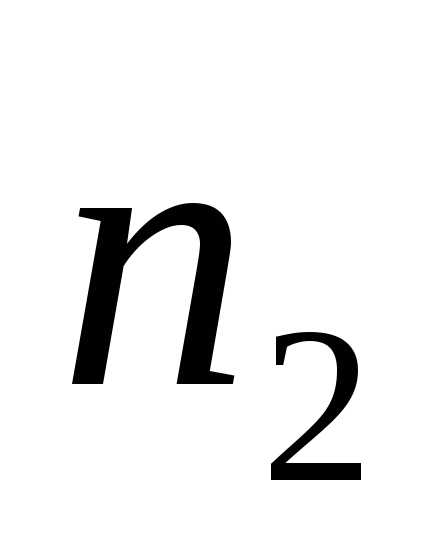 такое, что
такое, что
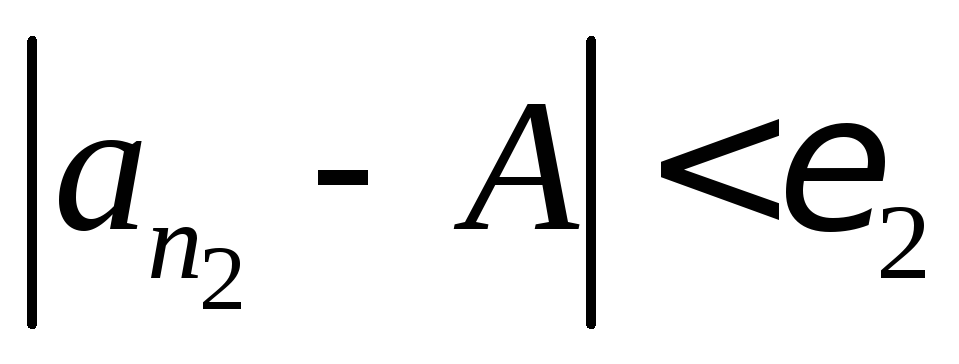 .
Точка
.
Точка
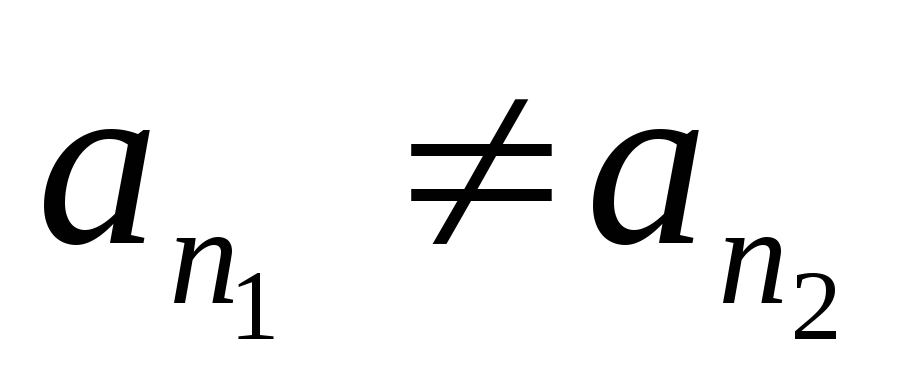 ,
т.к.
,
т.к.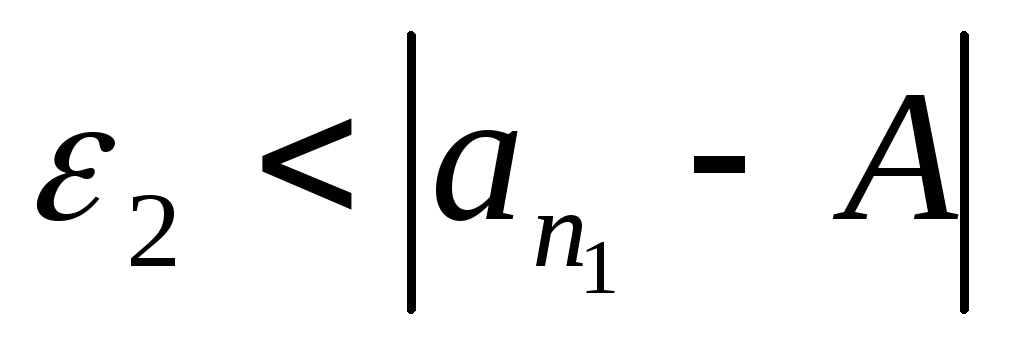 ,
а номер
,
а номер выбираем так, чтобы выполнялось
неравенство
выбираем так, чтобы выполнялось
неравенство
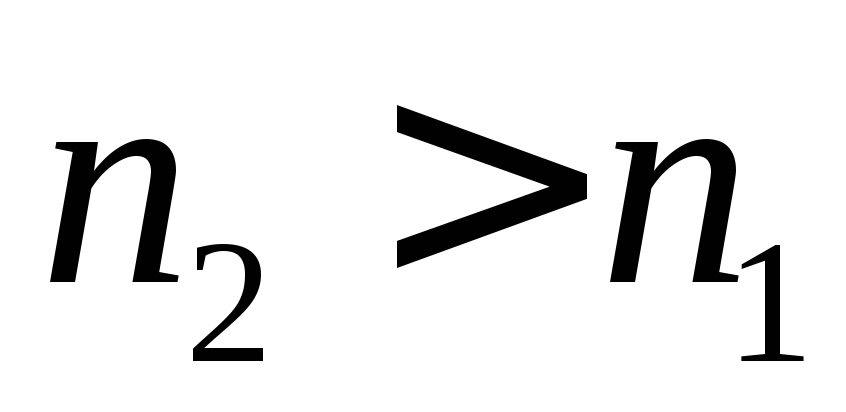 ,
что можно сделать, так как в любой
окрестности предельной точки содержится
бесконечное число элементов этого
множества. Далее,
,
что можно сделать, так как в любой
окрестности предельной точки содержится
бесконечное число элементов этого
множества. Далее,
 .
Как и раньше, строим
.
Как и раньше, строим
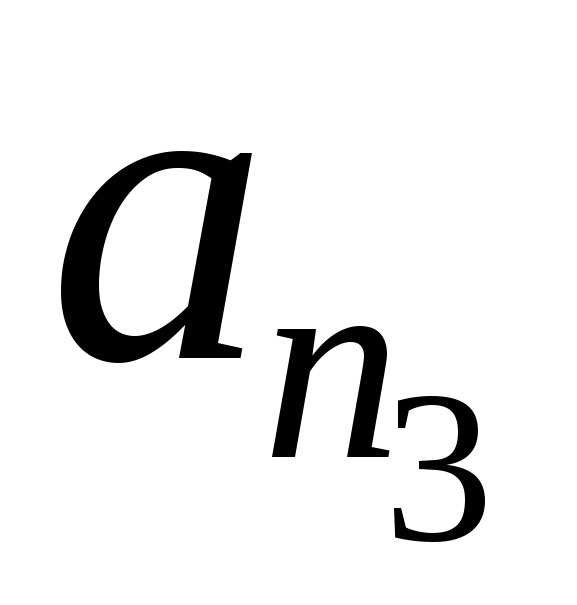 так,
что
так,
что
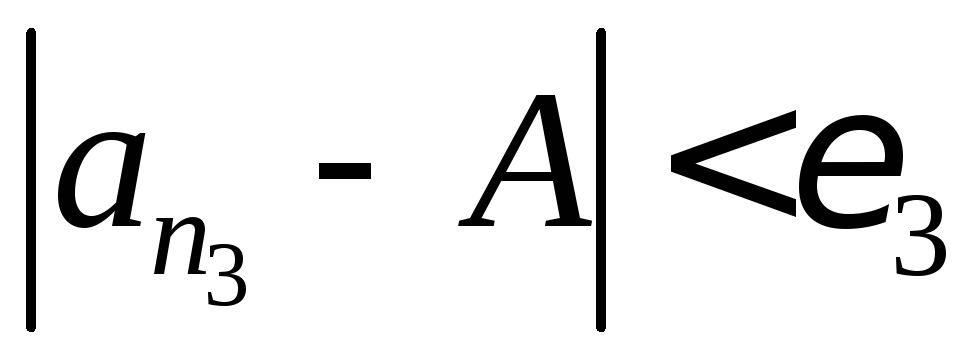 и
и
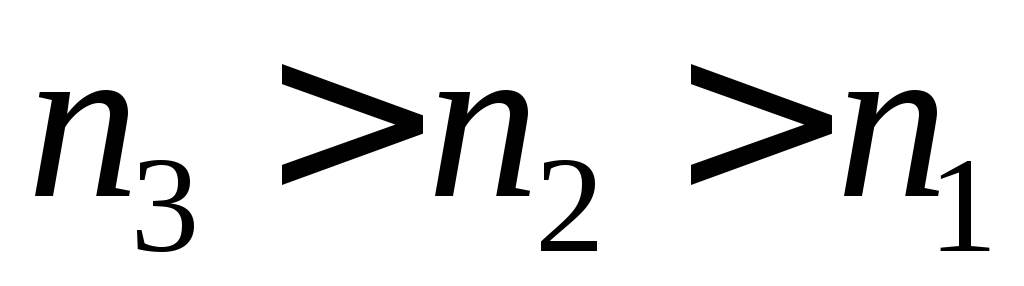 .
Продолжая этот процесс, получаем
последовательность
.
Продолжая этот процесс, получаем
последовательность
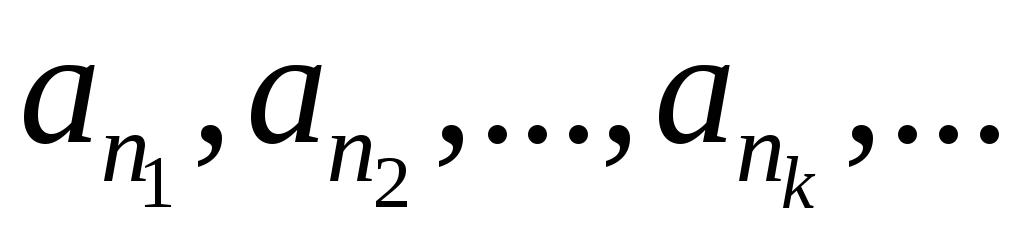 такую, что
такую, что
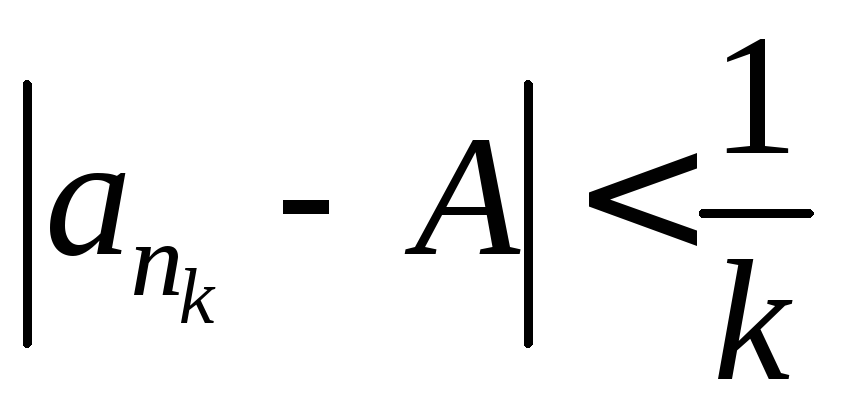 ,
что означает, что
,
что означает, что
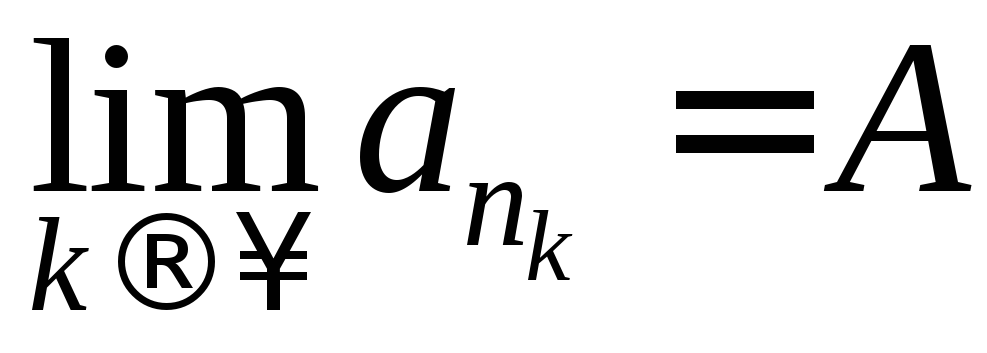 .►
.►
Определение
12.2.Последовательность
![]() называется
фундаментальной,
если для любого положительного
называется
фундаментальной,
если для любого положительного![]() существует такое
существует такое
![]() ,
что для всех
,
что для всех
![]() разность значений
разность значений
![]() по
модулю меньше
по
модулю меньше![]() ,
т.е.
,
т.е.
![]() .
.
Теорема 12.3 (Критерий Коши для последовательности) Предел последовательности существует тогда и только тогда, когда эта последовательность является фундаментальной.
◄Необходимость
![]()
То,
что последовательность имеет предел,
запишем так:
![]() .
Легко видеть, что
.
Легко видеть, что
![]() .
По свойству модулей:
.
По свойству модулей:
![]() .
Обозначив
.
Обозначив
![]() ,
имеем:
,
имеем:
![]() ,
т.е. из существования предела
последовательности легко следует ее
фундаментальность.
,
т.е. из существования предела
последовательности легко следует ее
фундаментальность.
Достаточность
![]()
Во-первых,
из фундаментальности последовательности
следует ее ограниченность. Действительно,
пусть
![]() .
Тогда существует
.
Тогда существует
![]() такое, что для всех
такое, что для всех
![]() имеет место неравенство
имеет место неравенство
![]() .
Положим
.
Положим
![]() .
Тогда для всех
.
Тогда для всех
![]()
![]() ,
т.е.
,
т.е.
![]() .
Пусть
.
Пусть
![]() .
Из этих неравенств тогда следует, что
при
.
Из этих неравенств тогда следует, что
при
![]() имеем:
имеем:
![]() .
Положим
.
Положим![]() .
Теперь для всех
.
Теперь для всех
![]() имеет
место неравенство
имеет
место неравенство
![]() ,
т.е.
,
т.е.![]() - ограниченная последовательность.
- ограниченная последовательность.
По
теореме 12.2 существует подпоследовательность
![]() такая, что она имеет некоторый предел
такая, что она имеет некоторый предел
![]() , т.е.
, т.е.
![]() .
Докажем, что вся последовательность
имеет тот же предел, т.е . что
.
Докажем, что вся последовательность
имеет тот же предел, т.е . что
![]() ,
для чего достаточно доказать, что
,
для чего достаточно доказать, что
![]() .
.
У
нас доказано, что
![]() ,
что
,
что
![]() .
.
Если
![]() и если
и если
![]() ,
то
,
то
![]() ,
поэтому
,
поэтому
![]() ,
что и требовалось доказать.
►
,
что и требовалось доказать.
►
Теорема
12.4 (Критерий
Коши для функции) Условие:
для любого
![]() существует
такое
существует
такое
![]()
![]() ,
что для любых
,
что для любых
![]() из
из
![]() разность значений функции
разность значений функции
![]() в этих точках по абсолютной величине
меньше
в этих точках по абсолютной величине
меньше![]() ,
равносильно тому, что существует предел
этой функции при
,
равносильно тому, что существует предел
этой функции при
![]() ,
т.е.
,
т.е.
![]() .
(1)
.
(1)
◄Необходимость![]()
Пусть
существует предел
![]() .
Тогда
.
Тогда
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() ,
,
![]() .
Следовательно,
.
Следовательно,![]() .
.
Достаточность![]()
Доказательство достаточности значительно труднее и его не обязательно рассказывать на экзамене.
Однако для заинтересованного читателя ниже приводится схема этого доказательства.
Сначала
дадим ещё одно определение предела
функции при
![]() .
.
Определение
12.3(
предела
функции
![]() при
при
![]() по Гейне
). Говорят, что функция
по Гейне
). Говорят, что функция
![]() имеет
при
имеет
при
![]() предел
предел
![]() ,если
для любой последовательности
,если
для любой последовательности
![]() такой,
что
такой,
что![]() и такой, что для всех
и такой, что для всех![]() выполнено неравенство
выполнено неравенство![]() ,
предел
,
предел![]() .
.
Теорема 12.5. Определение 8.3, т.е. определение предела по Коши, равносильно определению 12.3 предела по Гейне.
◄ Пусть
сначала функция имеет предел по Коши.
Рассмотрим произвольную последовательность
![]() такую, что
такую, что![]() и такую, что для всех
и такую, что для всех![]() выполнено неравенство
выполнено неравенство![]() .
По определению предела по Коши,
.
По определению предела по Коши,
![]() . По определению предела последовательности,
. По определению предела последовательности,
![]() .Значит,
при
.Значит,
при
![]() выполняется
условие
выполняется
условие
![]() ,из
которого сразу следует неравенство
,из
которого сразу следует неравенство
![]() , означающее, что
, означающее, что![]() ,
Тем самым, предел этой функции по Гейне
также существует.
,
Тем самым, предел этой функции по Гейне
также существует.
Предположим
теперь, что предел по Коши не существует
и докажем, что не существует и предел
по Гейне. По предположению, существует
такое число
![]() ,что
для любого числа
,что
для любого числа
![]() существует такая точка
существует такая точка![]() ,
что
,
что![]() .
Последовательно выбирая в качестве
.
Последовательно выбирая в качестве![]() числа
числа![]() ,
находим точки
,
находим точки![]() такие, что
такие, что![]() .
Эти
точки представляют собой последовательность
точек, удовлетворяющую всем условиям,
входящим в определение предела по Гейне,
однако для этой последовательности
условие
.
Эти
точки представляют собой последовательность
точек, удовлетворяющую всем условиям,
входящим в определение предела по Гейне,
однако для этой последовательности
условие
![]() не
выполнено.►
не
выполнено.►
Докажем теперь, что из условия (1) вытекает, что функция имеет предел по Гейне.
Действительно,
возьмём
любую последовательность
![]() такую,
что
такую,
что![]() и такую, что для всех
и такую, что для всех![]() выполнено неравенство
выполнено неравенство![]() .
Рассмотрим соответствующую
последовательность
.
Рассмотрим соответствующую
последовательность![]() .
Зафиксируем
.
Зафиксируем![]() и выберем соответствующее
и выберем соответствующее![]() с помощью (1). Так как
с помощью (1). Так как![]() ,
имеем:
,
имеем:![]() .
Далее, при
.
Далее, при
![]()
![]() и ,по условию (1) ,
и ,по условию (1) ,
![]() .Значит,
.Значит,
![]() -фундаментальная
последовательность. По теореме 12.3
существует предел последовательности
-фундаментальная
последовательность. По теореме 12.3
существует предел последовательности![]() ,
обозначим его
,
обозначим его![]() .
.
Осталось
доказать, что если взять любую другую
последовательность
![]() такую,
что
такую,
что
![]() и такую, что для всех
и такую, что для всех
![]() выполнено неравенство
выполнено неравенство
![]() ,
то
,
то![]() .
.
Для
этого рассмотрим последовательность
![]() .
Это – последовательность точек,
сходящаяся к точке
.
Это – последовательность точек,
сходящаяся к точке
![]() и
не принимающая значение
и
не принимающая значение![]() ,
согласно своему определению. Поэтому
последовательность значений
,
согласно своему определению. Поэтому
последовательность значений![]() также имеет предел, по доказанному выше.
Тогда по теореме 12.1 предел этой
последовательности равен пределу
подпоследовательности
также имеет предел, по доказанному выше.
Тогда по теореме 12.1 предел этой
последовательности равен пределу
подпоследовательности![]() и пределу подпоследовательности
и пределу подпоследовательности![]() ,
равному
,
равному![]() .►
.►
