
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
Вопрос 3: отображения и их свойства
Определение
3.1.Назовём
бинарное отношение
![]() функциональным,
если для каждого
функциональным,
если для каждого
![]() сечение
сечение![]() содержит не более одного элемента.
содержит не более одного элемента.
Определение
3.2.Если
отношение
![]() ,
симметричное к отношению
,
симметричное к отношению![]() ,
также является функциональным, то
отношение
,
также является функциональным, то
отношение![]() называетсявзаимно
однозначным.
называетсявзаимно
однозначным.
Определение
3.3.Если
для каждого
![]() сечение
сечение![]() содержит ровно один элемент, то
функциональное отношениевсюду
определено.
содержит ровно один элемент, то
функциональное отношениевсюду
определено.
С функциональным отношением непосредственно связано понятие отображения.
Определение
3.4.Отображение,
обозначим его![]() ,
сопоставляет каждому элементу, называемомуаргументом
отображения,
для которого сечение
,
сопоставляет каждому элементу, называемомуаргументом
отображения,
для которого сечение
![]() - непустое множество, единственный
элемент
- непустое множество, единственный
элемент![]() подмножества
подмножества![]() множества
множества![]() .
Этот элемент
.
Этот элемент![]() называетсяобразом
элемента
называетсяобразом
элемента
![]() при отображении
при отображении![]() .
.
Множество
тех элементов
![]() ,
для которых существует
,
для которых существует![]() ,
называетсяобластью
определения
отображения
,
называетсяобластью
определения
отображения
![]() .
.
Определение
3.5.Если
отображение
![]() определено на всём множестве
определено на всём множестве![]() ,
то говорят, что заданоотображение
,
то говорят, что заданоотображение
![]() в
в
![]() .
.
Определение
3.6.Множество
образов элементов
![]() при отображении
при отображении![]() называетсяобразом
отображения.
Если
называетсяобразом
отображения.
Если
![]() ,
тообраз
,
тообраз
![]() определяется,
как множество образов элементов
определяется,
как множество образов элементов![]() .
.
Определение
3.7.Если
образ совпадает со всем множеством
![]() ,
то говорят, что заданоотображение
,
то говорят, что заданоотображение
![]() на
на![]() ,
или что
,
или что
![]() -сюръективное
отображение,
или сюръекция.
(При этом требование всюду определённости
не является обязательным).
-сюръективное
отображение,
или сюръекция.
(При этом требование всюду определённости
не является обязательным).
Определение
3.8.Если
![]() ,
то
,
то![]() обозначаетпрообраз
множества
обозначаетпрообраз
множества
![]() ,
т.е. множество тех элементов
,
т.е. множество тех элементов![]() ,
для которых
,
для которых![]() .
.
Отметим очевидные свойства образа и прообраза:
![]() .
.
Определение
3.9.Если
отношение
![]() является взаимно однозначным, то
отображение, соответствующее
является взаимно однозначным, то
отображение, соответствующее![]() ,
называетсяобратным
к
,
называетсяобратным
к
![]() и обозначается
и обозначается![]() .
Если при этом отношение
.
Если при этом отношение![]() всюду определено, то
всюду определено, то![]() называетсяинъективным
отображением,
или инъекцией.
Если, кроме того, отображение ещё и
сюръективно, то оно называется биективным
или биекцией.
называетсяинъективным
отображением,
или инъекцией.
Если, кроме того, отображение ещё и
сюръективно, то оно называется биективным
или биекцией.
Отметим,
что выше мы использовали обозначение
прообраза![]() и
в случаях, когда обратное к
и
в случаях, когда обратное к![]() отображение
отображение![]() не существует. Если же обратное отображение
существует, то прообраз
не существует. Если же обратное отображение
существует, то прообраз![]() можно рассматривать, как образ множества
можно рассматривать, как образ множества![]() при отображении
при отображении![]() .
.
Наиболее
часто встречающимся функциональным
отношением является обычная функция
![]() ,
определённая на некотором подмножестве
,
определённая на некотором подмножестве![]() числовой прямой, значения которой
образуют множество
числовой прямой, значения которой
образуют множество![]() .
Действительно, эту функциональную
зависимость можно трактовать, как
задание подмножества в множестве
.
Действительно, эту функциональную
зависимость можно трактовать, как
задание подмножества в множестве![]() ,
в которое входят те пары
,
в которое входят те пары![]() ,
для которых выполнено равенство
,
для которых выполнено равенство![]() .
Изображение этого множества пар на
плоскости носит название графика
функции.
.
Изображение этого множества пар на
плоскости носит название графика
функции.
Вопрос 4: множество действительных чисел. Аксиома отделимости
Предварительные сведения о натуральных, целых, рациональных числах. На экзамене содержание параграфов 1,2,3 следует знать, но можно не рассказывать. (Содержание параграфа 1΄ можно и не знать, сведения об аксиоматике Пеано приведены исключительно для общего развития).
§1. Натуральные числа
Натуральное число можно также отнести к тем понятиям, которые интуитивно ясны каждому человеку и, разумеется, свойства этих чисел известны из курса средней школы. В этом параграфе мы напомним эти свойства
Сложение натуральных чисел обладает следующими свойствами:
1.
![]() (ассоциативность, или сочетательный
закон).
(ассоциативность, или сочетательный
закон).
2.
![]() (коммутативность, или переместительный
закон).
(коммутативность, или переместительный
закон).
Для
натуральных чисел
![]() естественно вводится отношение порядкаменьше
или равно,
обозначаемое
естественно вводится отношение порядкаменьше
или равно,
обозначаемое
![]() ,
и для любых чисел
,
и для любых чисел![]() выполняется либо соотношение
выполняется либо соотношение![]() ,
либо
,
либо![]() .
.
Отношение порядка обладает такими свойствами:
Если одновременно
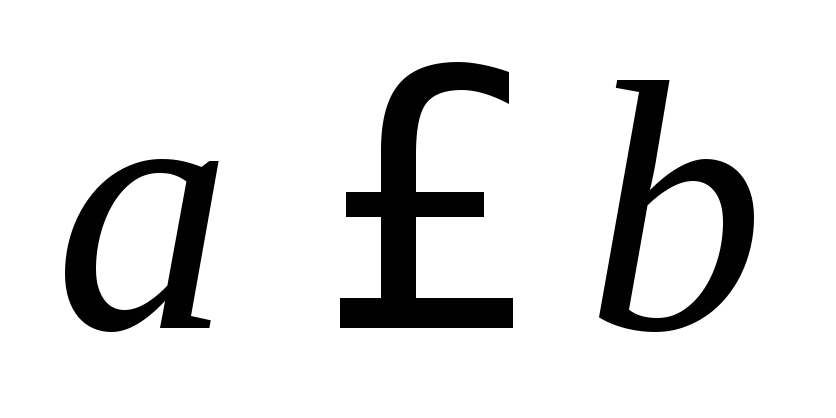 и
и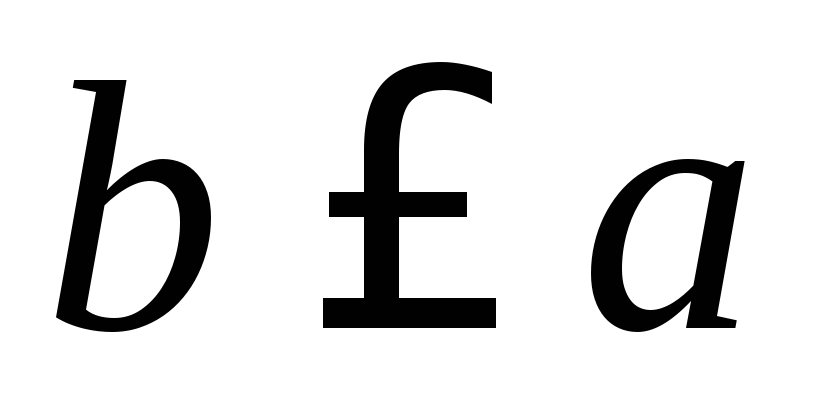 ,
то
,
то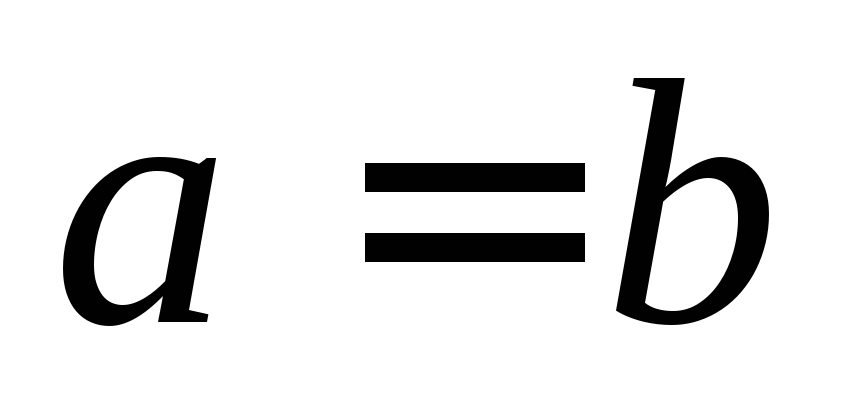 .
.Если
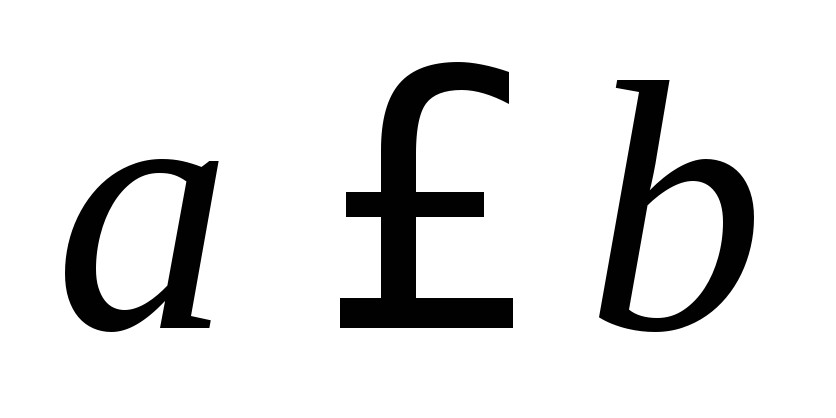 и
и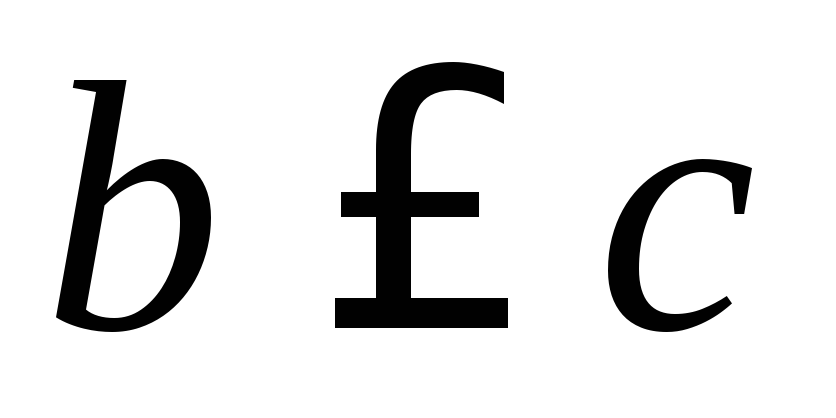 ,
то
,
то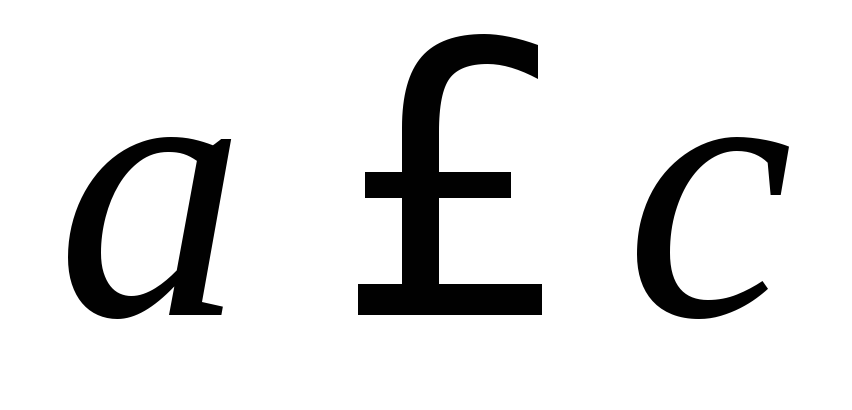 .
.Если
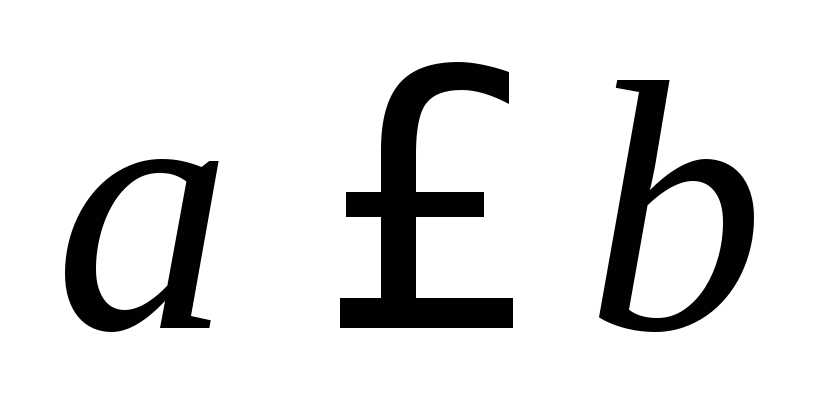 ,
то для всех
,
то для всех выполняется:
выполняется: .
.
Умножение натуральных чисел обладает следующими свойствами:
1.
![]() (ассоциативность, или сочетательный
закон).
(ассоциативность, или сочетательный
закон).
2.
![]() (коммутативность, или переместительный
закон).
(коммутативность, или переместительный
закон).
3.
Если
![]() ,
то для всех натуральных
,
то для всех натуральных![]() выполняется:
выполняется:![]() .
.
4.
![]() (дистрибутивность умножения относительно
сложения, или распределительный закон).
(дистрибутивность умножения относительно
сложения, или распределительный закон).
Множество натуральных чисел обозначается N.
Мы
не будем подробно останавливаться на
позиционных системах счисления, как
средствах для изображения чисел. В
школе, да и в большинстве вычислений,
используется привычная десятичная
система счисления. Отметим, однако, что
в ряде задач более удобны, например,
двоичная или троичная системы. Также в
качестве примера изобразим число 100 в
двоичной системе:1100100 ( так как 100=1
![]() 64+
1
64+
1![]() 32+0
32+0![]() 16+
0
16+
0![]() 8+1
8+1![]() 4+0
4+0![]() 2+0
2+0![]() 1).
1).
