3. Выпуклость дважды дифференцируемой функции

Теорема 30.3. Для того чтобы функция f, дважды дифференцируемая в интервале (a,b), была выпуклой вниз (вверх) на (a,b), необходимо и достаточно, чтобы во всех точках.

◄ Согласно критерию монотонности функции на промежутке (теорема29.1), условие для всехявляется необходимым и достаточным условием возрастания (убывания) производной функцииf’(x) на . Последнее свойство, согласно теореме 30.1 предыдущего пункта, является необходимым и достаточным условием выпуклости вниз (вверх) функции f на интервале .►

4.Точки перегиба

Определение 30.2. Точку кривой ,называютточкой перегиба, если она отделяет участок кривой, где функция выпукла вверх, от участка кривой, где функция выпукла вниз.

Если функция дифференцируема на интервале , то по теореме 30.1 в некоторой окрестности абсциссыточки перегиба её производная либо возрастает слева от точки, а справа от неё убывает, либо - наоборот. В первом случае рассматриваемая точка будет точкой максимума производнойf’(x), во втором случае – точкой минимума. Если предположить существование , то по теореме 23.1 (Ферма), применённой к функцииf’(x), получим: =0.

Это условие играет такую же роль в отношении точек перегиба, какую играло условие в отношении точек экстремума, т.е. оно является необходимым, но не достаточным. Действительно, функция, очевидно, выпукла вниз, но её вторая производная, равная, обращается в ноль при.

Достаточное условие точки перегиба даёт следующее правило, вытекающее из теоремы 30.3:

если при переходе через значение вторая производнаяменяет знак, то налицо перегиб. Если же знак не меняется, то перегиба нет.

Используя формулу Тейлора, так же, как при исследовании функции на экстремум, можно доказать следующее утверждение:

если , и еслинечётное число, то в точкеимеется перегиб, если жечётное число, то перегиба нет.

Просьба перенумеровать, т.е заменить все 16. на 31.

31. Пространство , множества в нем.

Напомним, что арифметическое n-мерное пространство представляет собой множество точек Это векторное пространство с операциями суммы и произведения на число ,определяемыми так

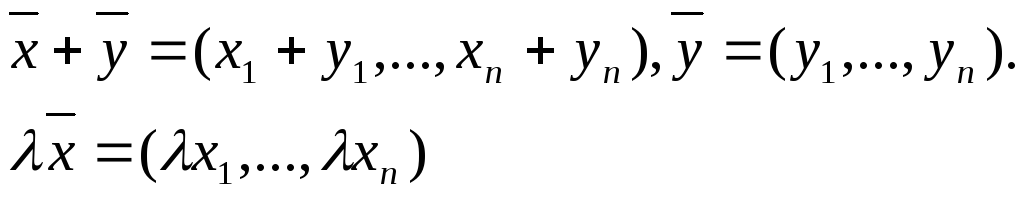
Более того это – евклидово пространство со скалярным произведением . Следовательно, определенанорма вектора , равная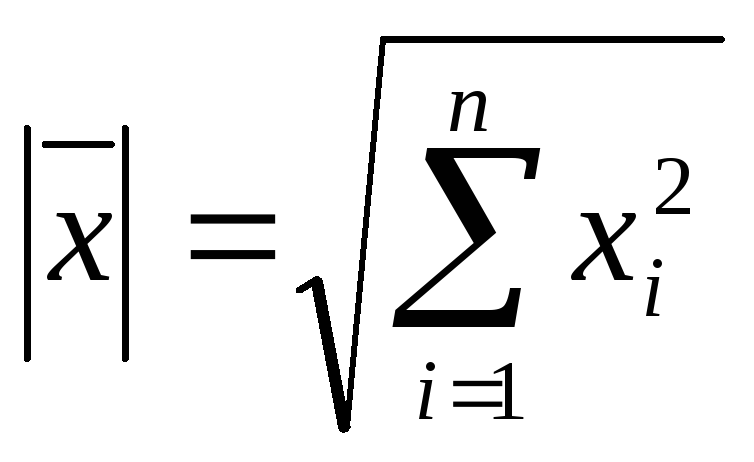и расстояние междуи,заданное формулой

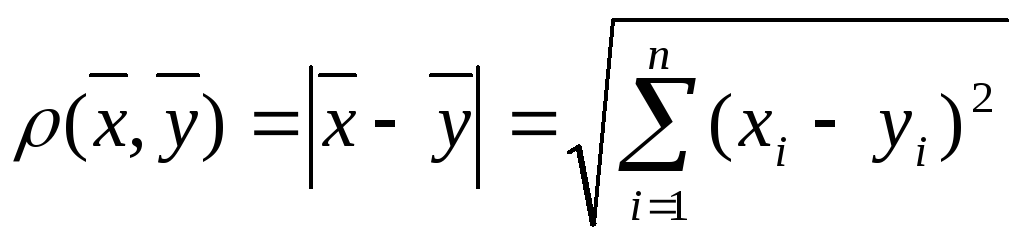(31.1)

При иэта формула становится очевидной формулой для расстояний на плоскости и в пространстве, поэтому общую формулу (31.1) для расстояния можно рассматривать какестественное обобщение известных формул на случай n-мерного пространства.

В курсе линейной алгебры было доказано:

1. , причем;

2. ;

3.

Свойство 3 называется неравенством треугольника.

Определение 31.1 Множество, на котором определена функция , обладающая свойствами 1-3, называетсяметрическим пространством, а -метрикой (или расстоянием) а этом пространстве.

Итак, - метрическое пространство с расстоянием (31.1).

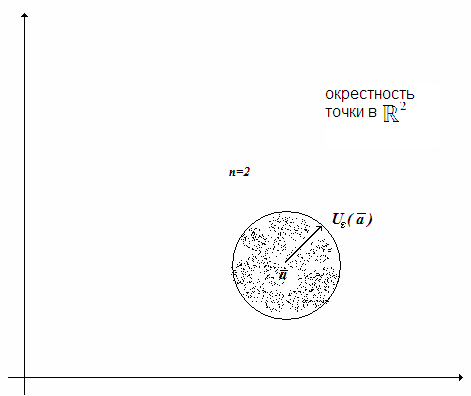
Определение 31.2 -окрестностью точки называется множество точек таких, что . Обозначим ее

Определение 31.3 Пусть . Тогда называетсявнутренней точкой этого множества, если .

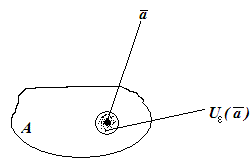
Определение 31.4 - открытое множество, если все его точки – внутренние.

Примеры: интервал в , круг без границы в .

(( ) )

Определение 31.5 Пусть . Точка называется предельной точкой множества, если.

Определение 31.6 называется замкнутым множеством, если оно содержит все свои предельные точки.

Примеры: отрезок в , круг с границей в .

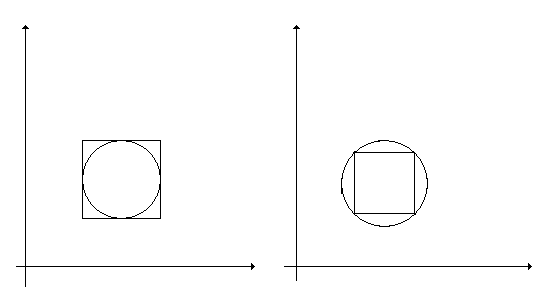
Замечание. Часто вместо «круглых» окрестностей рассматривают «прямоугольные», т.е. .

Легко видеть, что каждую «круглую» окрестность можно вписать в «прямоугольную» и наоборот.

Определение 31.7 Множество называетсякомпактным если из любой бесконечной системы открытых множеств такой, чтоможно выбрать конечное числотак, что .

Иными словами, из любого покрытия можно выделить конечное подпокрытие.

Теорема 31.1 компактно тогда и только тогда, когда оно ограниченное (т.е. содержится в некотором шаре с центром в начале координат) и замкнутое (без доказательства).