Вопрос 22.

Эластичность и её свойства.

Определение. Пусть функция y определена в некоторой окрестности точки x, дифференцируема в точке x и y(x) ≠ 0. Эластичностью функции y в точке x называется величина

(y) = (1)

Если предположить, что x , то можно рассматривать величину

, (2)

которая характеризует величину относительного изменения y в результате соответствующего относительного изменения x; например, процентное изменение спроса на товар в результате однопроцентного изменения цены этого товара. Тогда из (1) и (2) следует, что

Если y>0, то по теореме о производной сложной функции.

Если y<0, то ,

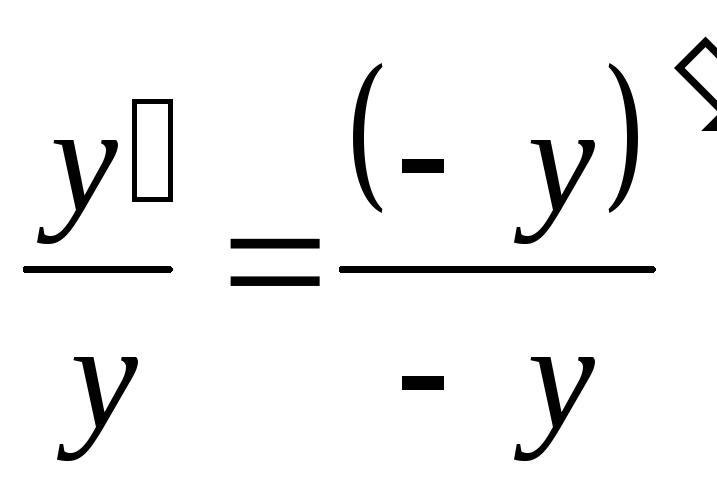поэтому при y<0

Следовательно, формулу (1) можно переписать в виде

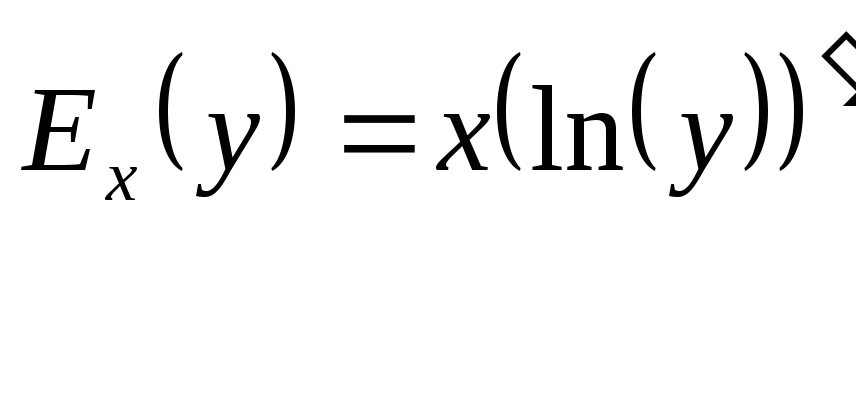при y>0

(3)

при y<0

Обе эти формулы можно объединить в одну : .

Теорема. 1) Если u, v – функции, для которых определены эластичности и,

То: =+,

(4)

-.

2) Если для функции y = y(x), определённой на интервале , существует обратная функцияx = x(y), причём y дифференцируема на этом интервале и ни в одной точкеx интервала не выполняется равенство , то для всехx0,y0 определены величиныи,

причём =(5)

◄По формуле

= ;

= Равенства (4) доказаны.

Далее, по теореме о производной сложной функции ,

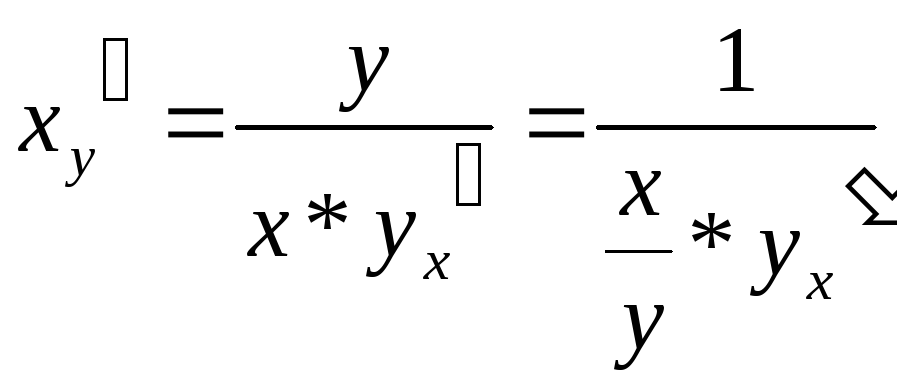что в соответствии с (1) даёт

, т.е (5) ►

В качестве примера рассмотрим ценовую эластичность спроса.

Пусть P – первоначальная цена товара, Q – первоначальное количество получаемой продукции, т.е. первоначальный спрос, - изменение цены,- соответствующее изменение спроса. Обычно при повышении цены, т.е. при>0, спрос на товар сокращается, т.е.<0, поэтому

и,

по теореме о предельном переходе в неравенствах, .

Величина эластичности в зависимости от цен представляет собой важную характеристику спроса на товар.

Спрос является эластичным, если . Причём уменьшение цен на 1% вызывает увеличение спроса меньше, чем на 1%.

При спросе с единичной эластичностью, т.е. , процент увеличения спроса равен проценту уменьшения цен товара.

Теорема. Пусть R(P) = P*Q(P) – выручка от реализации по цене P продукции в объёме Q(P) .

Пусть Q(P) – дифференцируемая функция. Если , т.е. если спрос эластичен, то с ростом цен выручка уменьшается, а с уменьшением цен – возрастает.

Если , т.е. если спрос неэластичен,, то с ростом цен выручка растёт, с уменьшением цен выручка уменьшается.

Если , то выручка не меняется с изменением цен.

Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума

Пусть - некоторая проколотая окрестность точки а.

Определение: Точка а – точка локального максимума f(x), если для всех xвыполняется неравенствоf(x)<f(a).Если для всех xвыполняется неравенство, то говорят о точкенестрогого максимума.

Аналогичным образом определяются точки локального минимума и нестрогого локального минимума. Следует только заменить входящие в определение неравенства неравенствами и, соответственно.

Обобщающие названия для точек максимума и минимума – точки экстремума.

Теорема 23.1(П. Ферма): Пусть функция y=f(x) определена в окрестности точки а, пусть эта точка – точка экстремума (хотя бы нестрогого) для функции f(x) и пусть существует производная Тогда=0.

◄Рассмотрим, для определенности, случай точки максимума. Тогда для всехxвыполняется неравенствоf(x)<f(a), или . Еслиxих<a, то .

По условию существует производная . Значит, существует. По теореме о предельном переходе в неравенствах,.

А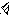налогично, приx,х>a выполняется неравенство , поэтому. Так как,==, должны выполняться неравенства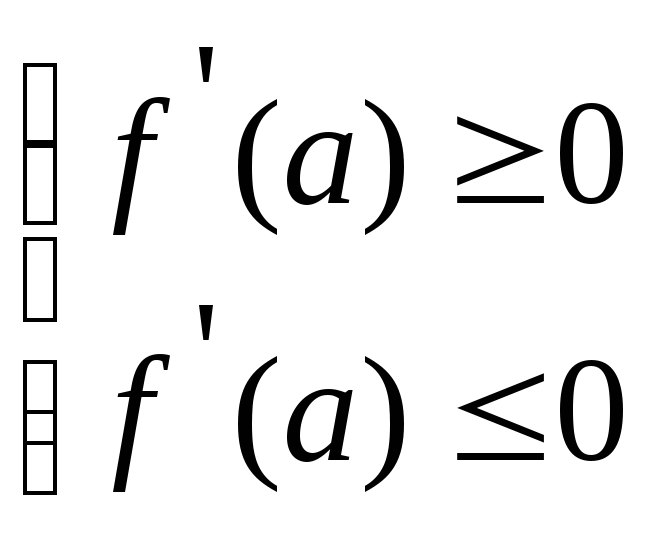, из которых следует доказываемое равенство=0. ►

Примечание 1. В точке экстремума производная может не существовать. Примером служит функция . Она имеет минимум в точке х=0. однако,ине существует.

Примечание 2. Теорема Ферма дает необходимое условие экстремума, но не достаточное, т.е. производная функции в точке может равняться нулю, а экстремума в этой точке нет. Пример: . Эта функция имеет производную, обращающуюся в ноль при х=0, однаковозрастает на всей числовой прямой.

Следствие (необходимые условия экстремума). Если функция непрерывна на (а;b), то точками локального экстремума могут быть только такие точки х₀ , в которых производная функции либо не существует, либо обращается в 0.

Теорема 23.2(М.Ролль) Пусть

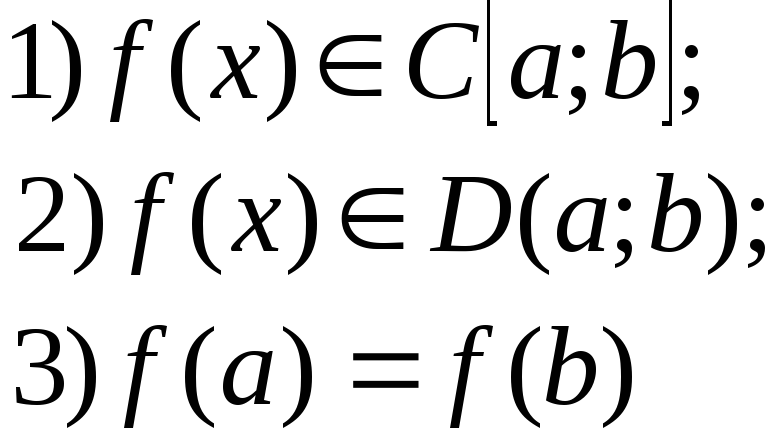
Тогда существует точка с(a;b) такая, что =0.

◄Так как функция f(x) непрерывна на отрезке [a;b], она принимает на этом отрезке наибольшее значение М и наименьшее значение m.

Если оказалось, что m=M, то это означает, что m=f(x)=M для всех x[a;b], т.е. функция - постоянная на [a;b]. Поэтому для всех х(a;b) имеет место равенство =0.

Если же mM, т.е. m<M, то хотя бы одно из этих значений функция принимает во внутренней точке [a;b].

Действительно, по условию 3) значения f(a) и f(b) равны друг другу и могут оказаться равны не более, чем одному из чисел m, M.

Пусть, например, М=f(c), где с(a;b). Так как М наибольшее значение функции f(x) на всем отрезке [a;b], то оно будет наибольшим и для x, т.е.с – точка локального экстремума.

По условию 2), в этой точке существует производная . По теореме Ферма,=0.►

Замечание 1. все условия теоремы Ролля являются существенными. Это означает, что если не выполняется одно из них, а остальные два выполняются, заключение теоремы может оказаться неверным.

Примеры. 1)

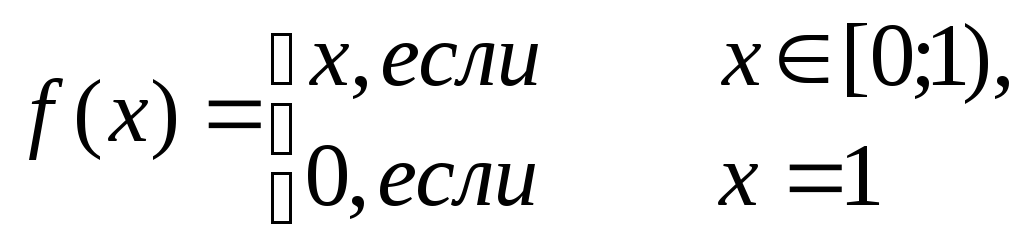
Выполнены условия 2) и 3), не выполнено условие 1). Для всех имеем=1.

2) f(x)=,x[-1;1].

Не выполнено условие 2), условия 1),3) выполнены. На интервале (-1;0): =-1; на интервале (0;1):=1. В точкеx=0 производная не существует, поэтому на (-1;1) нет такой точки, что =0

3) f(x)=x

Выполнены первые 2 условия, третье на отрезке [0;1] не выполнено. Всюду на (0;1) имеем =1.

Следствие теоремы 23.2: Пусть

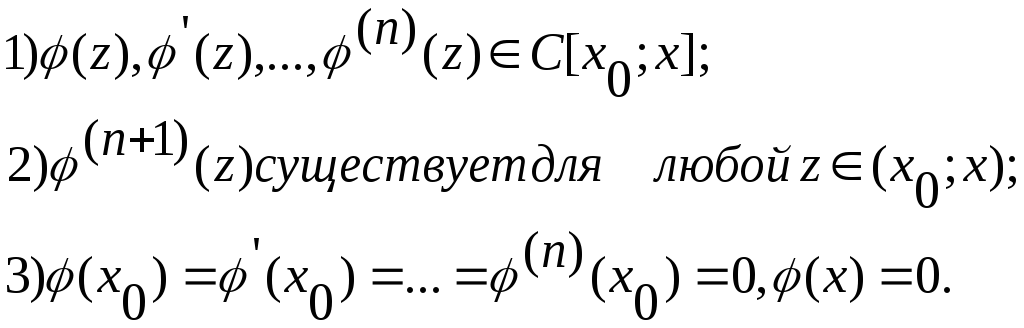
Тогда существует точка такая, что.

◄Для функции на отрезке [x₀;x] выполнены все условия теоремы Ролля, поэтому существует точка такая, что .

Рассмотрим функцию на отрезке [x₀;c₁]. Для нее также выполнены все условия теоремы Ролля. Поэтому существует точка с₂ , , такая что.

Аналогичными рассуждениями получаем, что существуют точки такие, чтоНаконец, рассмотрим функциюна отрезке [x₀;c_n]. она тоже удовлетворяет всем условиям теоремы Ролля, т.к. существует на (x₀;), значит и на (x₀;c_n). Поэтому, по теореме Ролля, существует точка такая, что.►

Замечание 2. Геометрический смысл теоремы Ролля: при ее условиях есть хотя бы одна точка с на интервале (а;b), касательная в которой параллельна оси x.