Вопрос 20: дифференциал. Инвариантность формы первого дифференциала

1.Понятие дифференциала числовой функции

Определение 1. Если числовая функция дифференцируема в точке , то ее дифференциалом в этой точке называют однородную линейную функцию (новой) независимой переменной .

Таким образом,

= (1)

Положив в формуле (1) , получим

(2)

так что дифференциал функции в каждой точке есть

тождественная функция. Подставляя (2) в правую часть (1), получаем

= , (3)

равенство двух линейных функций и . Из него следует, что часто используемое обозначение производной можно рассматривать, как отношение дифференциалови.

Функция определена для всех действительных значений . Однако по традиции часто рассматривают лишь на множестве тех , для которых принадлежит области определения функции; т.е., лишь на множестве приращений аргумента функции . Это объясняется тем, что дифференциал тесно связан с приращением функции. Так как, по предположению, дифференцируема в точке x, то

, (4)

где при и первое слагаемое в правой части (4) – дифференциал, но рассматриваемый только для . Если, то ,поэтому говорят, что «дифференциал есть главная линейная часть приращения функции».

2. Геометрический и механический смысл дифференциала.

Пусть числовая функция дифференцируема в точке . Как известно, ее график имеет в точке касательную с угловым коэффициентом .

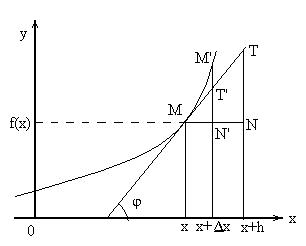
Теорема 20.1. Значение =дифференциала равно приращению ординаты этой касательной при переходе отк (см. рис.).

►Действительно, , ,поэтому . Из рисунка также видно, что есть часть приращения функции, стремящееся к совпадению с ним при .◄

Дифференциал допускает и механическое толкование. Если – время, а– путь, пройденный прямолинейно движущейся точкой к моменту , то - ее скорость в данный момент. Тогда равен длине пути, который прошла бы точка за промежуток времени от до , если бы ее скорость оставалась неизменной (т.е. приложенные силы уравновесились).

3. Инвариантность формы первого дифференциала

Правило дифференцирования сложной функции приведет нас к одному замечательному и важному свойству дифференциала.

Пусть функции итаковы, что из них может быть составлена сложная функция:. Если существуют производныеи, то по теореме 20.2 существует и производная

(5)

Дифференциал , еслисчитать независимой переменной, выразится по формуле (3). Перейдём теперь к независимой переменной; в этом предположении имеем другое выражение для дифференциала:

.

Заменяя производную её выражением (5) и замечая, чтоесть дифференциалкак функции от, окончательно получим:

,

т. е. вернёмся к прежней форме дифференциала.

Таким образом, мы видим, что

форма дифференциала может быть сохранена даже в том случае, если прежняя независимая переменная заменена новой.

Мы всегда имеем право писать дифференциал как в форме (1), будет линезависимой переменной или нет; разница лишь в том, что, если за независимую переменную выбрано, тоозначает не произвольное приращение, а дифференциалкак функции от. Это свойство и называютинвариантностью формы дифференциала.