
Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика
.pdf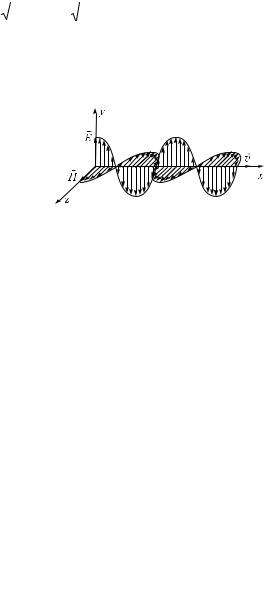
Колебания векторов E è H происходят с одинаковой фазой, а амплитуды этих векторов связаны соотношением
|
|
|
|
|
|
E m 0 H m 0 , |
(3.190) |
||||
т. е. по одному вектору однозначно определяется другой.
На рис. 3.44 представлено графическое изображение электромаг-
нитной волны, описываемой уравнениями (3.189). Электромагнитные
волны — поперечные волны, векторы E è H поля волны лежат в плоскости, перпендикулярной направле-
нию распространения волны. Кро-
ме того, векторы E è H поля волны
взаимно перпендикулярны, так что |
|
|||
|
|
и векторы |
|
|
вектор скорости волны v |
|
|||
|
|
|
|
|
E è H образуют правую тройку. |
|
|||
В фиксированной точке простран- |
|
|||
|
|
|
Ðèñ. 3.44 |
|
ства векторы E è H изменяются со |
||||
|
||||
временем по гармоническому за- |
|
|||
кону. Они одновременно увеличиваются от нуля, затем через 1/4 |
периода |
|
|
достигают наибольшего значения, причем если E направлен вверх, то H направлен вправо (смотрим вдоль направления распространения волны). Еще через 1/4 периода оба вектора одновременно обращаются в нуль. За-
тем опять достигают наибольшего значения, но на этот раз вектор E íà-
правлен вниз, а H — влево. И, наконец, по завершении периода колеба-
ния векторы снова обращаются в нуль. Такие изменения векторов E è H происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками, отсчитанными вдоль оси x.
Распространение всякой волны связано с переносом энергии. Элек-
тромагнитные волны также переносят энергию. Плотность потока энергии
можно получить, умножив плотность энергии w на скорость v (см. форму-
лу (1.156)). В случае электромагнитных волн вектор плотности потока |
|||||||
|
|
|
|
|
|
|
|
энергии принято обозначать буквой S. Следовательно, модуль вектора S |
|||||||
|
S = w v. |
|
|
|
(3.191) |
||
Плотность энергии электромагнитного поля слагается из плотностей |
|||||||
энергии электрического (3.58) и магнитного (3.136) полей: |
|
||||||
w w |
w |
|
0 E 2 |
|
0 H 2 |
. |
(3.192) |
|
|
||||||
E |
H |
2 |
2 |
|
|
||
|
|
|
|
||||
171
В вакууме и в непроводящей среде векторы E è H изменяются в каждой точке пространства в одинаковой фазе. Поэтому соотношение (3.191) между амплитудами напряженностей электрического и магнитного полей справедливо и для их мгновенных значений.
Отсюда следует, что плотность энергии электрического и магнитно-
го полей в каждый момент времени одинакова: w |
w |
. Поэтому мож- |
||
но написать, что w 2w |
0 E 2 |
E |
H |
|
. Воспользовавшись тем, что |
||||
E |
|
|
|
|
E
 0 H
0 H 
 0 , выражению для плотности энергии электромагнитной волны можно придать следующий вид:
0 , выражению для плотности энергии электромагнитной волны можно придать следующий вид:
w 
 0 0 EH EH , v
0 0 EH EH , v
а для плотности потока энергии:
S wv EH .
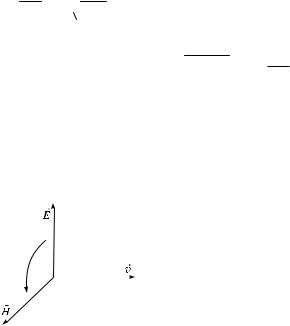
Векторы E è H взаимно перпендикулярны и образуют с направлени-
ем распространения волны правовинтовую систему (рис. 3.45). Поэтому |
|||||||
|
|
|
|
|
|
|
|
направление вектора E |
H совпадает с направлением переноса энергии, |
||||||
|
|
|
а модуль этого вектора равен ÅÍ. Следователь- |
||||
|
|
|
но, вектор плотности потока электромагнитной |
||||
|
|
|
энергии можно представить как векторное про- |
||||
|
|
|
|
|
|
|
|
|
|
|
изведение E è H : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
wv |
E |
H . |
(3.193) |
|
|
|
|
|
|
|
|
|
|
|
Вектор S называется вектором Пойнтин- |
||||
|
|
|
|
|
|
|
|
|
|
|
ãà. Поскольку векторы E è H изменяются со |
||||
Ðèñ. 3.45 |
|
временем по закону косинуса, модуль вектора |
|||||
|
|
|
Пойнтинга в каждой точке изменяется по зако- |
||||
|
|
|
ну квадрата косинуса. Среднее значение квад- |
||||
рата косинуса за период равно 1/2. Поэтому среднее значение плотности потока энергии — интенсивности волны I — будет следующее:
I = EmHm/2. |
(3.194) |
Поглощаясь в каком-либо теле, электромагнитная волна сообщает этому телу некоторый импульс, т. е. оказывает на него давление. Соответствующий расчет показывает, что в случае идеально поглощающей поверхности давление электромагнитной волны равно ее объемной
172
плотности энергии: p = w. Эта величина пульсирует с очень большой частотой. Поэтому практически может быть измерено ее среднее по времени значение. Таким образом,
p w . |
(3.195) |
Для идеально отражающей поверхности давление будет в два раза больше.
Световое давление было измерено П. Н. Лебедевым. Результаты измерений оказались в полном согласии с теорией Максвелла.
3.5.Вопросы для самоконтроля
1.Электрический заряд и его свойства. Закон сохранения электри- ческого заряда. Закон Кулона. Диэлектрическая проницаемость
èее физический смысл.
2.Электрическое поле. Напряженность поля. Поле точечного заряда. Графическое изображение электростатических полей. Принцип суперпозиции полей. Поле системы зарядов.
3.Энергетическая характеристика электростатического поля — потенциал. Потенциал поля точечного заряда и системы зарядов. Связь между напряженностью электрического поля и потенциалом.
4.Работа сил электростатического поля по перемещению зарядов. Циркуляция вектора напряженности. Потенциальный характер электростатического поля.
5.Поток вектора напряженности электростатического поля. Теорема Гаусса. Вычисление напряженности поля заряженных сферы
èшара с помощью теоремы Гаусса.
6.Теорема Гаусса. Вычисление поля заряженной плоскости, параллельных плоскостей с помощью теоремы Гаусса.
7.Поляризация диэлектриков. Вектор поляризованности. Электри- ческий диполь. Электрический момент диполя. Полярные и неполярные молекулы.
8.Свободные и связанные заряды. Электростатическое поле в диэлектриках. Диэлектрическая проницаемость и восприимчи- вость. Теорема Гаусса для электростатического поля в диэлектриках. Вектор электрического смещения.
173
9.Проводники в электрическом поле. Электростатическая защита. Электроемкость проводников. Конденсаторы. Соединение конденсаторов.
10.Энергия заряженного проводника. Энергия заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии.
11.Характеристики электрического тока: сила тока, вектор плотности тока. Законы Ома и Джоуля — Ленца в дифференциальной форме.
12.Основные характеристики электрической цепи: разность потенциалов, электродвижущая сила, напряжение, сопротивление.
13.Законы Ома для участков цепи. Соединение сопротивлений.
14.Работа, мощность и тепловое действие постоянного тока. Закон Джоуля — Ленца.
15.Разветвленные цепи. Правила Кирхгофа.
16.Магнитное поле и его характеристики: магнитная индукция и напряженность. Закон Био — Савара — Лапласа.
17.Применение закона Био — Савара — Лапласа к расчету магнитных полей токов. Поле прямолинейного и кругового проводников с током.
18.Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие параллельных токов. Единица силы тока в СИ — ампер.
19.Действие магнитного поля на движущийся заряд. Сила Лоренца.
20.Циркуляция вектора индукции магнитного поля. Вихревой характер магнитного поля. Напряженность магнитного поля. Закон полного тока. Магнитное поле соленоида.
21.Магнитный поток. Работа перемещения проводника и контура с током в магнитном поле.
22.Явление электромагнитной индукции. ЭДС индукции. Закон Фарадея. Правило Ленца. Практическая значимость явления электромагнитной индукции.
23.Явление самоиндукции, ЭДС самоиндукции, индуктивность контура.
24.Взаимная индукция. ЭДС взаимной индукции. Трансформаторы.
174
25.Энергия магнитного поля соленоида. Плотность энергии магнитного поля.
26.Намагничивание вещества. Вектор намагниченности. Магнитная проницаемость и магнитная восприимчивость.
27.Äèà-, пара- и ферромагнетики. Зависимость намагничивания ферромагнетиков от напряженности магнитного поля и температуры (гистерезис, точка Кюри).
28.Колебательный контур. Аналогия между механическими и электромагнитными колебаниями. Применение колебательного контура.
29.Переменный ток и его получение. Активное и реактивное сопротивление цепи. Мощность, выделяемая в цепи переменного тока.
30.Токи смещения. Вихревое электрическое поле. Система уравнений Максвелла в интегральной форме.
31.Уравнение плоской электромагнитной волны. Скорость распространения электромагнитных волн в средах.
32.Энергия электромагнитной волны. Вектор Пойнтинга. Шкала электромагнитных волн.
4. ОПТИКА
Оптика — раздел физики, изучающий свойства и физическую природу света, а также его взаимодействие с веществом.
Свет представляет собой сложное явление: в одних случаях он ведет себя как волна, в других — как поток особых частиц (фотонов). Двойственная природа света называется корпускулярно-волновым дуализмом.
Волновая оптика — раздел оптики, в котором свет рассматривается как электромагнитная волна, занимающая диапазон шкалы электромагнитных волн от 1 до 105 нм, включающих ультрафиолетовую (1–400 нм), видимую (400–750 нм) и инфракрасную (750–105 нм) области спектра. В волновой оптике изучаются явления интерференции, дифракции и поляризации.
Квантовая оптика — раздел оптики, в котором свет рассматривается как поток фотонов.
Однако многие оптические явления, в частности действие оптиче- ских приборов, можно рассматривать исходя из представления о световых лучах (геометрическая èëè лучевая оптика).
4.1. Элементы геометрической оптики
Геометрическая оптика — раздел оптики, в котором изучаются законы распространения света на основе представлений о световых лучах. Под световым лучом понимают линию, вдоль которой распространяется поток световой энергии.
Основные законы геометрической оптики
В рамках геометрической оптики могут быть поняты простейшие оптические явления, например возникновение теней и получение изображений в оптических приборах. В ее основе лежат четыре закона, установленных опытным путем: 1) закон прямолинейного распространения света; 2) закон независимости световых пучков; 3) закон отражения è 4) закон преломления света.
176
Согласно закону прямолинейного распространения света, ñâåò
âпрозрачной однородной среде распространяется по прямым линиям. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами, освещаемыми точечными источ- никами света, т. е. источниками, размеры которых малы по сравнению с размерами освещаемого тела и расстоянием до него.
Закон независимости световых пучков состоит в том, что распространение всякого светового пучка совершенно не зависит от того, есть
âней другие пучки света или нет. Световой пучок, прошедший через ка- кую-либо область пространства, выходит из нее одним и тем же, независимо от того, заполнена она другим светом или не заполнена. Закон независимости световых пучков необходимо дополнить утверждением, определяющим совместное действие световых пучков при их наложении друг на друга. Оно состоит в том, что освещенность экрана, создаваемая несколькими световыми пучками, равна сумме освещенностей, создаваемых каждым пучком в отдельности.
На основе законов прямолинейного распространения и независимости световых пучков и сложилось представление о световых лучах. В математическом смысле ëó÷ есть линия, вдоль которой распространяется свет. Это — математическая абстракция. Реальное существование имеют не математические лучи и бесконечно тонкие пучки света, а пучки конечного поперечного сечения, вырезаемые, например, диафрагмами. Поэтому под лучом в физическом смысле этого слова понимают конечный, но достаточно узкий световой пучок, который еще может существовать изолированно от других пучков.
Когда луч достигает плоской границы раздела двух прозрачных сред, он частично проходит во вторую среду (преломляется), частично возвращается обрат-
но (отражается). |
|
Закон отражения утверждает, что падаю- |
|
щий и отраженный лучи лежат в одной плос- |
|
|
|
кости с нормалью n к границе раздела в точке |
|
падения (эта плоскость называется плоско- |
|
стью падения), причем угол падения равен уг- |
|
лу отражения (ðèñ. 4.1). |
|
Закон преломления был установлен экспе- |
|
риментально в 1621 г. голландским ученым |
|
Снеллиусом: преломленный луч лежит в плос- |
Ðèñ. 4.1 |
177

кости падения, причем отношение синуса угла падения к синусу угла преломления для данных сред есть величина постоянная, не зависящая от угла падения (см. рис. 4.1), т. е.
sin |
n21 . |
(4.1) |
|
||
sin |
|
|
Постоянная величина n21 называется относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называется абсолютным показателем преломления этой среды. Его обозначают через n, снабжая эту букву, если требуется, соответствующими индексами. Например, n1 — показатель преломления первой среды, а n2 — второй. Относительный показатель преломления n21 выражается через абсолютные показатели n1 è n2 соотношением
n21 n2 n1 . |
(4.2) |
Cвет преломляется из-за различной скорости его распространения в разных средах. Абсолютный показатель преломления среды n показывает, во сколько раз скорость распространения света v в среде меньше, чем скорость света c в вакууме:
n c v. |
(4.3) |
Значение n для слабо поглощающих (прозрачных) твердых тел меняется от 1,3 до 4,0; для жидкостей — от 1,2 до 1,9; для газов (при нормальных условиях) — от 1,000035 (Не) до 1,000702 (Xe).
Показатель преломления характеризует оптическую плотность
среды. Среда с большим n называется оптически более плотной, чем среда с меньшим n (которая в этом случае называется оптически менее плотной).
На рис. 4.1 показан пример падения луча из среды, оптически менее плотной, в среду, оптически более плотную, при этом (в соответствии с законом (4.1)).
При переходе света из оптически более плотной среды в оптически менее плотную луч отклоняется от нормали к поверхности (рис. 4.2). Увеличение угла падения сопровождается более быстрым ростом угла преломления и по достижении углом значения
ïð arcsinn21 |
(4.4) |
178
угол становится равным /2. Величину ïð |
|
|
называют предельным углом падения. Ïðè óã- |
|
|
лах падения, больших ïð, свет во вторую сре- |
|
|
ду не проникает, интенсивность отраженного |
|
|
луча равна интенсивности падающего. Это яв- |
|
|
ление называется полным внутренним отра- |
Ðèñ. 4.2 |
|
жением. |
||
|
||
Явление полного отражения света исполь- |
|
|
зуется в различных областях науки и техники — от поляризационных |
||
устройств до световодов (оптоволокно). |
|
|
Линзы
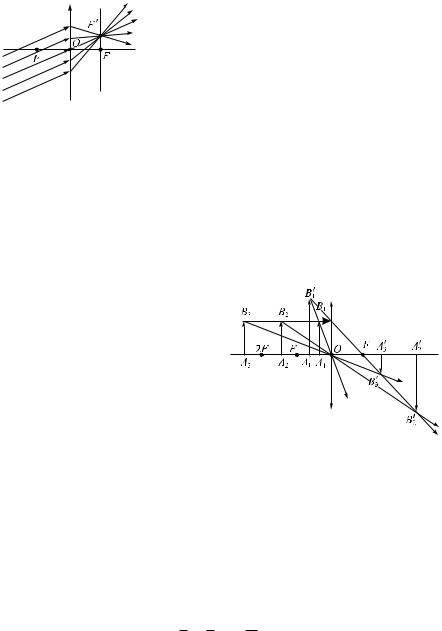
Линза — прозрачное тело, ограниченное криволинейными (обычно сферическими) поверхностями (рис. 4.3). Прямая, проходящая через центры O1 è O2 образующих сфер, называется главной оптической осью. Если толщина линзы d
много меньше радиусов R1 è R2 соответствующих сфер, то такая линза называется тонкой.
По способности отклонять проходящие лу-
чи тонкие линзы разделяются на собирающие è рассеивающие, схематическое обозначение и ход лучей которых приведены на рис. 4.4, à è á соответственно.
Точка O пересечения главной оптической оси с тонкой линзой называется оптическим центром линзы. Лучи, проходящие через оптический центр, не преломляются. Пучок лучей, параллельных главной оптиче- ской оси собирающей линзы, преломляясь на линзе, пересекается в од-
Ðèñ. 4.4
179
|
|
|
|
ной точке — главном фокусе линзы F. Äëÿ ðàñ- |
|||
|
|
|
|
сеивающей линзы в фокусе пересекаются про- |
|||
|
|
|
|
должения лучей (см. рис. 4.4). У каждой линзы |
|||
|
|
|
|
имеется 2 главных фокуса. Плоскость, перпен- |
|||
|
|
|
|
дикулярная главной оптической оси и прохо- |
|||
|
|
|
|
дящая через фокус, называется фокальной. |
|||
|
|
Ðèñ. 4.5 |
|
Прямая, проходящая через оптический центр |
|||
|
|
|
линзы, не совпадающая с главной оптической |
||||
|
|
|
|
||||
|
|
|
|
осью, называется побочной оптической осью. |
|||
Точка пересечения побочной оптической оси с фокальной плоскостью |
|||||||
называется побочным фокусом F. Пучок лучей, параллельных побочной |
|||||||
оптической оси собирающей линзы, преломляясь на линзе, пересекается |
|||||||
в побочном фокусе линзы F (ðèñ. 4.5). |
|
|
|||||
|
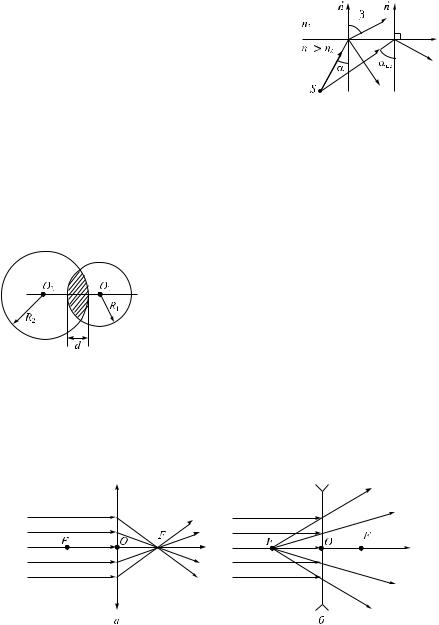
Построение изображений на примере собирающей линзы приведе- |
||||||
но на рис. 4.6. Если предмет A1B1 разместить от линзы на расстоянии |
|||||||
меньше фокусного, то лучи от каждой точки предмета после преломле- |
|||||||
ния на линзе окажутся расходящи- |
|
|
|||||
мися, но их продолжения в обрат- |
|
|
|||||
ную сторону пересекаются в точ- |
|
|
|||||
êàõ |
расположения |
изображения. |
|
|
|||
Такое |
изображение |
называется |
|
|
|||
мнимым. Итак, изображение A1B1 |
|
|
|||||
предмета A1B1 оказывается мни- |
|
|
|||||
мым. По рис. 4.6 также видно, что |
|
|
|||||
îíî |
|
оказывается |
увеличенным |
|
|
||
и прямым (неперевернутым). Ес- |
|
|
|||||
ли предмет A2B2 разместить между |
|
Ðèñ. 4.6 |
|||||
|
|
||||||
фокусом и точкой, расположен- |
|
|
|||||
ной от линзы на расстоянии, равном удвоенному фокусному, то изобра- |
|||||||
жение A2 B2 оказывается действительным, увеличенным и переверну- |
|||||||
тым. И, наконец, если предмет A3B3 разместить за двойным фокусным, |
|||||||
то изображение A3 B3 |
будет действительным, уменьшенным и пере- |
||||||
вернутым. |
|
|
|
|
|
||
|
Расстояние до изображения можно рассчитать по формуле тонкой |
||||||
линзы: |
|
|
|
|
|
||
|
|
|
|
1 1 1 , |
(4.5) |
||
|
|
|
|
a |
b |
f |
|
180 |
|
|
|
|
|
|
|
