Задачи контрольной работы
Даны координаты
точек
.
Требуется:
записать векторы
и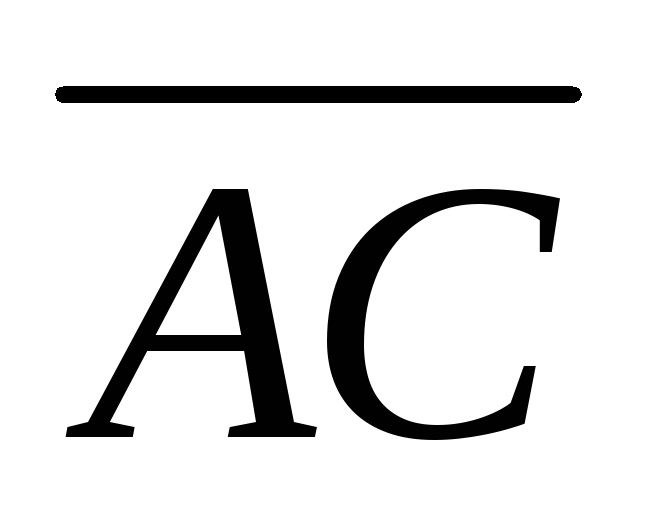
в системе орт
и
найти длины этих векторов;найти орт вектора
;изобразить векторы
и
в координатной плоскости
;найти вектора
и
аналитически и геометрически.
|
2.1 А(-8; -3), В(4; -12), С(8; 10) |
2.11 А(4; 0), В(7; 4), С(8; 2)
|
|
2.2 А(-5; 7), В(7; -2), С(11; 20)
|
2.12 А(-2; 7), В(10; -2), С(8; 12)
|
|
2.3 A(3; -1), В(7; 1), С(4; -2) |
2.13 А(-6; 8), В(6; -1), С(4; 13)
|
|
2.4 А(-12; -1), В(0; -10), С(4; 12)
|
2.14 А (0; 2), В(3; 6), С(4; 4)
|
|
2.5 А(-10; 3), В(2; 0), С(6; 22)
|
2.15 А(-10; 5), В(2; -4), С(0; 10)
|
|
2.6 А(0; 0), В(3; 4), С(4; 2)
|
2.16 А(-4; 12), В(8; 3), С(6; 17)
|
|
2.7 А(-9; 6), В(3; -3), С(7; 19)
|
2.17 А(-3; 10), В(9; 1), С(7; 15)
|
|
2.8 А(3; -3), В(6; 1), С(7; -1) |
2.18 А(4; -3), В(7; 1), С(8; -1)
|
|
2.9 А(1; 0), В(13; -9), С(17; 13)
|
2.19 А(2; -2), В(5; 2), С(6; 0)
|
|
2.10 А(0; 2), В(12; -7), С(16;15)
|
2.20 А(-1; 1), В(2; 5), С(3; 3)
|
2.2.Элементы векторной алгебры в пространстве Решение типового примера
Пример 2.2.
Даны координаты вершин пирамиды ABCD. Пусть А(0; 0; 1), В( 2; 3; 5), С(6; 2; 3), D(3; 7; 2).
Требуется:
Записать векторы
в системе орт
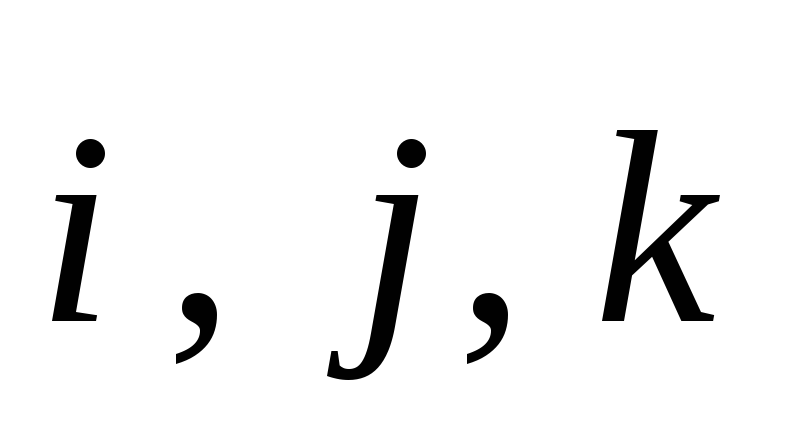и найти модули этих векторов;Найти угол между векторами
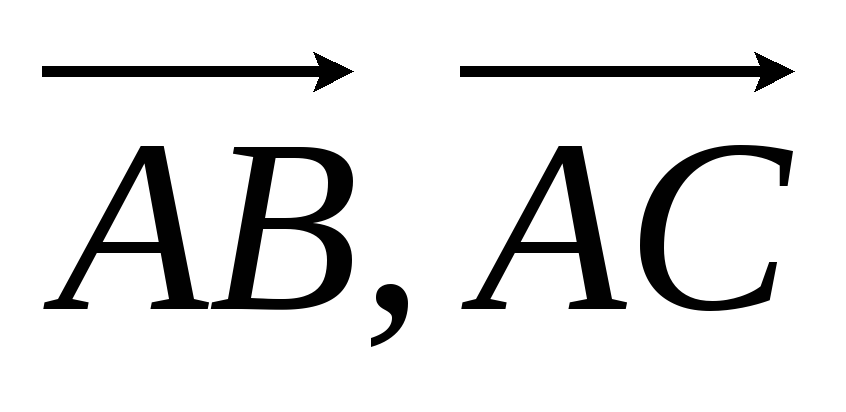;Найти проекцию вектора
на вектор
;Найти площадь грани АВС;
Найти объём пирамиды ABCD;
Решение.
1. Известно, что
произвольный вектор
представляется в системе орт
по формуле
(1)
где
координаты вектора
в системе координат, порождённой ортами,
причём
Если заданы точки
,
то для вектора
то есть
(2)
Воспользовавшись формулой (2) и координатами заданных точек A, B, C, D, получим:
Если вектор
задан формулой (1),то его модуль вычисляется
следующим образом:
(3)
Используя формулу (3), получаем модули найденных векторов:
Известна формула
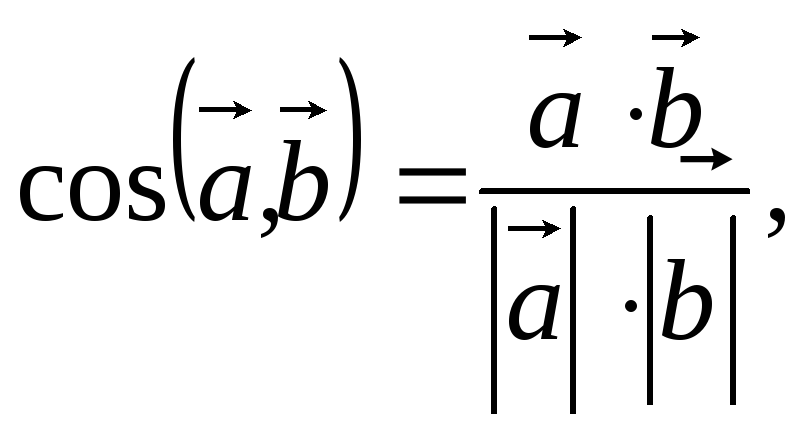
где
скалярное произведение векторов
и
,
которое можно вычислить следующим
образом:
У нас
то есть
.
3. Известно, что
,
то есть в нашем случае
4. Воспользуемся
формулой нахождения площади треугольника,
построенного на векторах
и
где
векторное произведение векторов,
которое можно вычислить по следующему
правилу:
.
В нашем примере
,
причём
Таким образом,
(кв. ед.).
Объём пирамиды,
построенной на трёх некомпланарных
векторах
можно найти по формуле
где
смешанное произведение векторов,
которое вычисляется следующим образом:
.
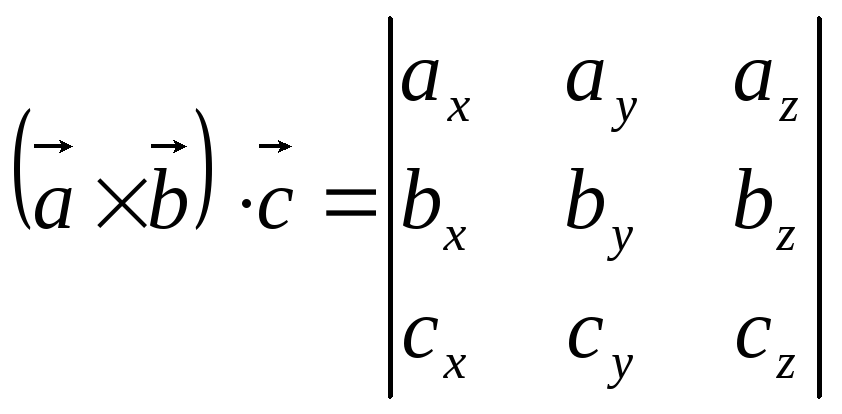У нас
,
где
,
то есть
(куб.ед.).
Задачи контрольной работы
Даны координаты вершин пирамиды ABCD.
Требуется:
Записать векторы
в системе орт
и найти модули этих векторов;Найти угол между векторами
;Найти проекцию вектора
на вектор
;Найти площадь грани АВС;
Найти объём пирамиды ABCD.
С(4; 8; -9), D(2; -1; 2).
|
2.11 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
2.12 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
2.13 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
2.14 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
2.18 A(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|
С(4; 8; -9), D(2; -1; 2).
|