
algebra10_нелін_дворівн
.pdf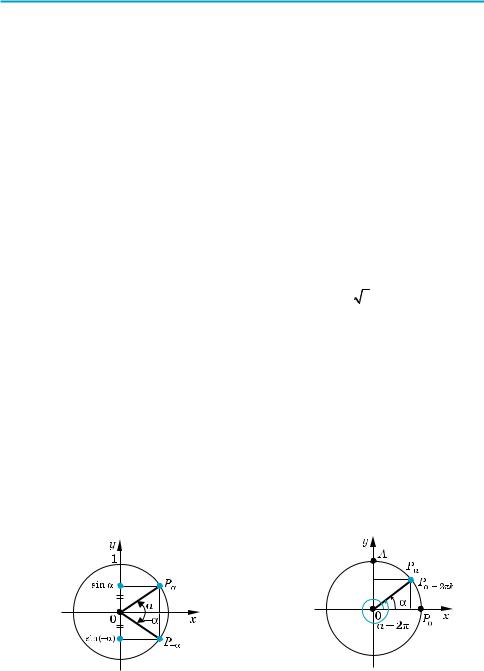
§ 4. Властивості тригонометричних функцій
Оскільки tgα = |
sinα |
і ctgα = |
cos α |
, то tg α > 0 і ctg α > 0 там, де sin α і cos α |
|
sin α |
|||||
cosα |
|||||
|
|
|
мають однакові знаки, тобто в I і III чвертях, tg α < 0 і ctg α < 0 там, де sin α
і cos α мають різні знаки, тобто в II і IV чвертях (рис. 41). )
2.Парність і непарність тригонометричних функцій.
(Щоб дослідити тригонометричні функції на парність і непарність, зазна
чимо, що на одиничному колі точки Pα і P–α розміщено симетрично віднос но осі Ox (рис. 42). Отже, ці точки мають однакові абсциси і протилежні
ординати. Тоді cos(−α )= xP−α = xPα = cosα, sin(−α )= yP−α = −yPα = − sinα. Таким чином, cos x — парна функція, а sin x — непарна.
Тоді tg(−α ) = |
sin(−α ) |
|
= − sinα = − tgα; |
ctg(−α ) = |
cos(−α ) |
= |
cos α |
= − ctgα. |
|
cos (−α ) |
sin(−α ) |
− sin α |
|||||||
|
cos α |
|
|
|
|||||
Отже, tg x і ctg x — непарні функції. )
Парність і непарність тригонометричних функцій можна використову вати для обчислення значень тригонометричних функцій від’ємних кутів
(чисел). |
)= − sin |
|
|
|
|
cos(− |
|
)= cos |
|
|
|
|
|
Наприклад, X sin(− |
π |
π |
= − |
1 |
, |
π |
π |
= |
2 |
. Y |
|||
|
|
|
|
2 |
|||||||||
6 |
6 |
2 |
|
4 |
4 |
|
|
||||||
3. Періодичність тригонометричних функцій. Багато процесів і явищ, що відбуваються в природі і техниці, мають повторюваний характер (наприклад, рух Землі навколо Сонця, рух маховика). Для опису такого роду процесів використовують так звані періодичні функції.
Функція y = f (x) називається періодичною з періодом T ≠ 0, якщо для
будь!якого x із області визначення функції числа (x + T) і (x – T) також належать області визначення і виконується рівність
f (x + T) = f (x – T) = f (x).
(Враховуючи, що на одиничному колі числам (кутам) α і α + 2πk, де k Z,
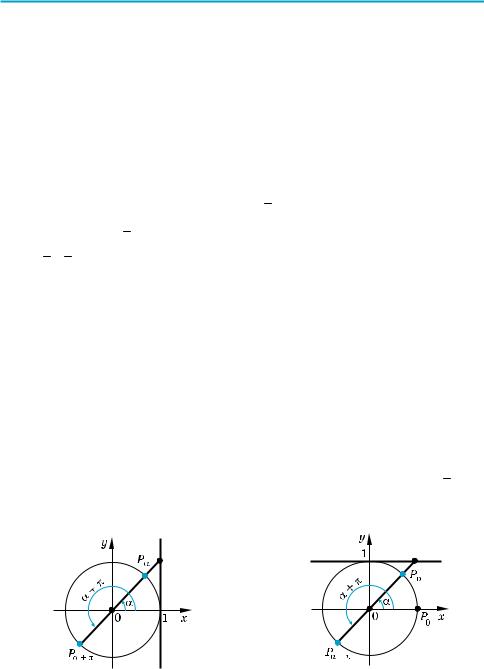
відповідає та сама точка (рис. 43), одержуємо
sin (α + 2πk) = sin α, cos (α + 2πk) = cos α. Тоді 2πk (k ≠ 0) є періодом функцій sin x і cos x.
Рис. 42 |
Рис. 43 |
51
РОЗДІЛ 1. Тригонометричні функції
При k = 1 одержуємо, що T = 2π — це період функцій sin x і cos x. Доведемо, що ці функції не можуть мати меншого додатного періоду. Щоб довести, що T = 2π — найменший додатний період косинуса, припустимо, що T > 0 — період функції cos x. Тоді для будь якого значення x вико нується рівність cos (x + T) = cos x. Взявши x = 0, одержуємо cos T = 1. Але це означає, що на одиничному колі при повороті на кут T точка P0 знову потрапляє в точку P0, тобто T = 2πk, де k Z. Отже, будь який період коси нуса повинен бути кратним 2π, а значить,
2π — найменший додатний період косинуса. )
(Щоб обґрунтувати, що T = 2π — найменший додатний період функції sin x,
досить у рівності sin (x + T) = sin x, яка виконується для будь яких зна чень x, взяти x = π2 . Одержуємо sin(T + 2π )= 1. Але це означає, що при пово
роті на кут T + π точка P потрапляє в точку A (0; 1) (рис. 43), тобто
2 0
T + π = π + 2πk, отже, T = 2πk. Таким чином, будь який період синуса пови
22
нен бути кратним 2π, а значить,
2π — найменший додатний період синуса. )
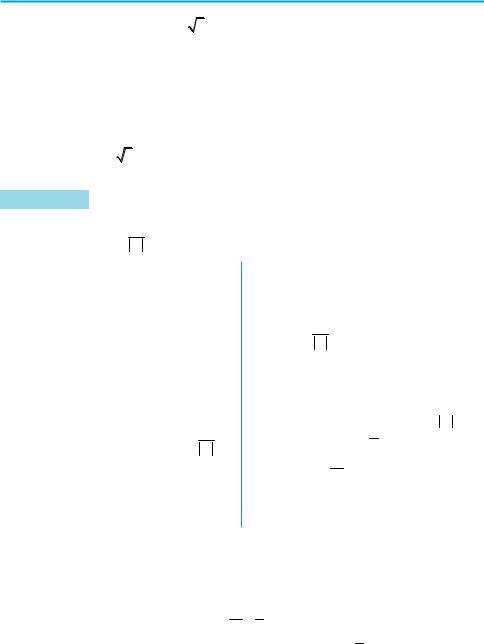
(Якщо врахувати, що на одиничному колі точки Pα і Pα + π є діаметрально протилежними, то цим точкам відповідає та сама точка на лінії тангенсів
(рис. 44) або на лінії котангенсів (рис. 45). Тоді tg (α + π) = tg α, ctg (α + π) = ctg α, а також tg (α + πk) = tg α, ctg (α + πk) = ctg α.
Тобто періодом функцій tg x і ctg x є πk (k ≠ 0, k Z).
Найменшим додатним періодом для функцій tg x і ctg x є T = π.
Щоб довести це, досить у рівності tg (x + T) = tg x взяти x = 0. Тоді одержує мо tg T = 0. Отже, T = πk, де k Z. Таким чином, будь який період тангенса повинен бути кратним π, а значить, π — найменший додатний період тан генса. Аналогічно у відповідній рівності для ctg x досить взяти x = π. )
2
(Щоб мати уявлення про поведінку графіка періодичної функції y = f (x), згадаємо, що за означенням графік функції y = f (x) складається з усіх то
Рис. 44 |
Рис. 45 |
52

§ 4. Властивості тригонометричних функцій
Рис. 46
чок M координатної площини, які мають координати (x; y) = (x; f (x)). Перша координата для точок графіка вибирається довільно з області ви значення функції. Виберемо як першу координату значення x + T (або в узагальненому вигляді — значення x + kT при цілому значенні k) і вра хуємо, що для періодичної функції f (x + T) = f (x – T) = f (x) (у загальному випадку f (x + kT) = f (x)). Тоді до графіка функції y = f (x) буде входити також точка M1 координатної площини з координатами:
(x + T; y) = (x + T; f (x + T)) = (x + T; f (x)).
Точку M1 (x + T; f (x)) можна одержати з точки M (x; f (x)) паралельним перенесенням уздовж осі Ox на T одиниць (рис. 46). У загальному випадку точку M2 (x + kT; f (x)) можна одержати з точки M (x; f (x)) паралельним перенесенням уздовж осі Ox на kT одиниць. Отже, через проміжок T ви гляд графіка періодичної функції буде повторюватися. Тому для побудови
графіка періодичної функції з періодом T досить побудувати графік на будь!якому проміжку довжиною T (наприклад, на проміжку [0; T]), а потім одержану лінію паралельно перенести праворуч і ліворуч уздовж осі Ox на відстані kT, де k — будь!яке натуральне число. )
Приклади розв’язання завдань
Приклад 1 Користуючись періодичністю, парністю і непарністю тригоно метричних функцій, знайдіть:
1) sin |
21π |
; |
2) cos (–405°); 3) tg |
16π |
; 4) ctg (–570°). |
|
|
||||
2 |
|
3 |
|
||
Ро з в ’ я з а н н я
1)X sin 212π = sin(10π + 2π )=
=sin(5 2π + 2π )= sin 2π = 1. Y
2)X cos(−405°)= cos405° =
= cos(360° + 45°)= cos45° = 2 . Y
2
Ко м е н т а р
1)Враховуючи, що значення функції sin x повторюються через період 2π,
виділимо в заданому аргументі число, кратне періоду (тобто 10π),
апотім скористаємося рівністю sin (α + 2πk) = sin α (k Z).
2)Спочатку враховуємо парність ко синуса: cos (–α) = cos α, а потім
його періодичність із періодом 2π = 360°: cos (α + 360°) = cos α.
53
РОЗДІЛ 1. Тригонометричні функції
|
16π |
|
π |
π |
= 3. |
Y |
|
||
3) X tg 3 = tg(5π + |
|
3 )= tg |
3 |
3) Функція тангенс періодична з пе |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ріодом π, тому виділяємо в задано |
|
|
|
|
|
|
|
|
|
му аргументі число, кратне періо |
|
|
|
|
|
|
|
|
|
ду (тобто 5π), а потім використо |
4) X ctg (–570°) = –ctg 570° = |
|
вуємо рівність tg (α + πk) = tg α. |
|||||||
|
4) Спочатку враховуємо непарність |
||||||||
= –ctg (540° +30°) = |
|
|
|
котангенса: ctg (–α) = –ctg α, |
|||||
= – ctg (180°æ3 + 30°) = |
|
|
|
а потім його періодичність із пе |
|||||
= − ctg 30° = − |
3. Y |
|
|
|
ріодом π =180°: |
||||
|
|
|
|
|
|
|
|
|
ctg (α + 180°æk) = ctg α. |
Приклад 2* Доведіть твердження: якщо функція y = f (x) періодична з пе!
ріодом T, то функція y = Af (kx + b) також періодична з періо! дом Tk (A, k, b — деякі числа і k ≠ 0).
Д о в е д е н н я
X Нехай ϕ (x) = Af (kx + b) і T = |
T |
. |
|
|
|
||
1 |
k |
|
|
|
|
||
Тоді ϕ (x + T1) = Af (k(x + T1) + b) =
= Af k x + |
|
T |
|
+ b |
= Af (kx ± T + b)= |
||
|
|
|
|
||||
|
|
k |
|
|
|
|
|
|
|
|
|||||
=Af (kx + b ± T)= Af(kx + b)= ϕ(x),
аце й означає, що функція
ϕ (x) = Af (kx + b) має період
T1 = Tk . Y
К о м е н т а р
За означенням функція ϕ (x) = = Af (kx + b) буде періодичною з пері
одом T1 = Tk , якщо для будь якого x
з області визначення ϕ значення цієї функції в точках x і x + T1 рівні, тобто ϕ (x + T1) = ϕ (x). У процесі обґрунту
вання враховано, що вираз k |
T |
при |
|
k |
|||
|
|
k > 0 дорівнює k T = T, а при k < 0
k
дорівнює k T = −T. Також врахова
−k
но, що функція f (x) за умовою періо дична з періодом T, і тому f (x1 ä T) = = f (x1), де x1 = kx + b.
Використаємо результат, одержаний у прикладі 2, для знаходження пе ріодів функцій.
Наприклад,
1) X якщо функція sin x має період T = 2π, то функція sin 4x має період
T1 = 2π = π ; Y
4 2
2) X якщо функція tg x має період T = π, то функція tg x має період
|
|
π |
4 |
|
T1 |
= |
= 4π. Y |
||
|
||||
|
1 |
|
||
|
4 |
|
||
54
§ 4. Властивості тригонометричних функцій
Запитання для контролю
1. а) Назвіть знаки тригонометричних функцій у кожній з координатних чвертей.
б*) Обґрунтуйте знаки тригонометричних функцій у кожній з координат них чвертей.
2. а) Які з тригонометричних функцій є парними, а які непарними? Наведіть приклади використання парності і непарності для обчислення значень тригонометричних функцій.
б*) Обґрунтуйте парність чи непарність відповідних тригонометричних функцій.
3.а) Яка функція називається періодичною? Наведіть приклади.
б*) Обґрунтуйте періодичність тригонометричних функцій. Укажіть най
менший додатний період для синуса, косинуса, тангенса і котангенса та обґрунтуйте, що в кожному випадку цей період дійсно є найменшим додатним періодом.
Вправи
1.Користуючись періодичністю, парністю і непарністю тригонометричної функції, знайдіть:
2)sin (–750°); (− 19π); 4) ctg 945°;1) cos 19π; 3) tg
3 |
|
|
( |
6 |
) |
|
||
4 |
|
|
4 |
|
||||
5) sin |
25π |
; |
6) cos (–3630°); 7) ctg |
|
− |
17π |
; |
8) tg 600°. |
|
|
|
||||||
2*. Серед заданих функцій знайдіть періодичні і вкажіть найменший додат ний період для кожної з них:
1) f (x) = x2; 2) f (x) = sin 2x; 3) f (x) = | x |; 4) f (x) = tg 3x; 5) f (x) = 3. 3. Знайдіть період кожної з заданих функцій:
1) y = cos 2x; 2) y = tg 5x; 3) |
y =sin |
x |
; |
4) y = ctg 3x; 5) |
y =cos |
2x |
. |
|
|
||||||
|
3 |
|
|
5 |
|
||
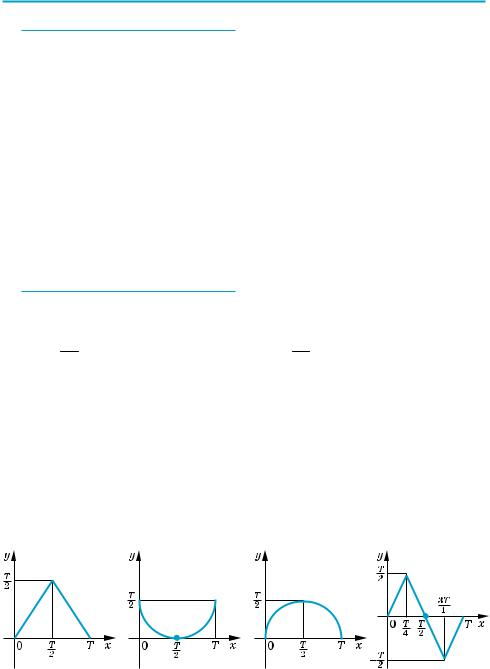
4.На кожному з рисунків 47–50 наведена частина графіка деякої періодич ної функції з періодом T. Продовжіть графік на відрізок [–2T; 3T].
Рис. 47 |
Рис. 48 |
Рис. 49 |
Рис. 50 |
55
§5 |
ГРАФІКИ ФУНКЦІЙ СИНУСА, КОСИНУСА, ТАНГЕНСА |
І КОТАНГЕНСА ТА ЇХ ВЛАСТИВОСТІ |
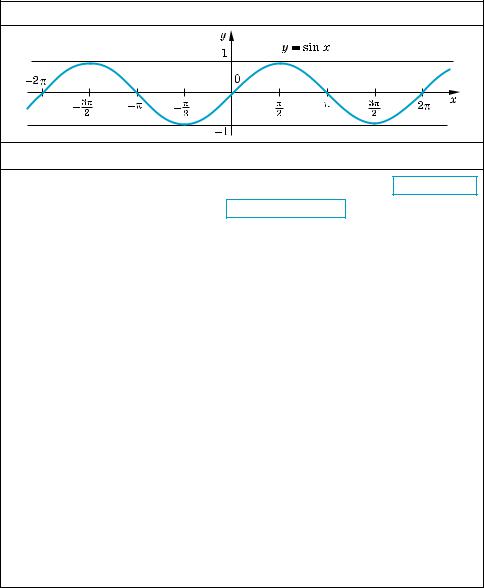
5.1. ГРАФІК ФУНКЦІЇ y = sin x ТА ЇЇ ВЛАСТИВОСТІ
Т а б л и ц я 10
Графік функції y = sin x (синусоїда)
Властивості функції y = sin x
1.Область визначення: x R (x — будь яке дійсне число). D (sin x) = R
2.Область значень: y [–1; 1]. E (sin x) = [–1; 1]
3.Функція непарна: sin (–x) = –sin x
(графік симетричний відносно початку координат).
4. |
Функція періодична з періодом |
T = 2π |
: |
|
sin (x + 2π) = sin x. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x = 0, |
|
|
|
|
|
|
y = 0, |
|
||||
5. |
Точки перетину з осями координат: |
Oy |
y = 0 |
|
|
Ox |
|
x = πk, k Z |
|
||||||||||
6. |
Проміжки знакосталості: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
sin x > 0 при x (2πk; π + 2πk), k Z |
|
|
|
|
|
|
|
|
|||||||||
|
|
sin x < 0 при x (π + 2πk; 2π + 2πk), k Z |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
Проміжки зростання і спадання: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
π |
|
||
|
функція sin x зростає на кожному з проміжків |
− |
|
|
+ 2πk; |
|
+ 2πk , k Z, |
||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
π |
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
||
|
і спадає на кожному з проміжків |
|
+ 2πk; |
|
+ 2πk , k Z. |
||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||||
8. |
Найбільше значення функції дорівнює 1 при x = |
π |
+ |
2πk, k Z. |
|||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
Найменше значення функції дорівнює –1 при x = − |
π + 2πk, k Z. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
56
§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості
Пояснення й обґрунтування
Характеризуючи властивості функцій, ми будемо найчастіше виділяти такі їх характеристики: 1) область визначення; 2) область значень; 3) парність чи непарність; 4) періодичність; 5) точки перетину з осями координат; 6) про міжки знакосталості; 7) проміжки зростання і спадання*; 8) найбільше та найменше значення функції.
З а у в а ж е н н я. Абсциси точок перетину графіка функції з віссю Ох (тоб то ті значення аргументу, при яких функція дорівнює нулю) називають нуля( ми функції.
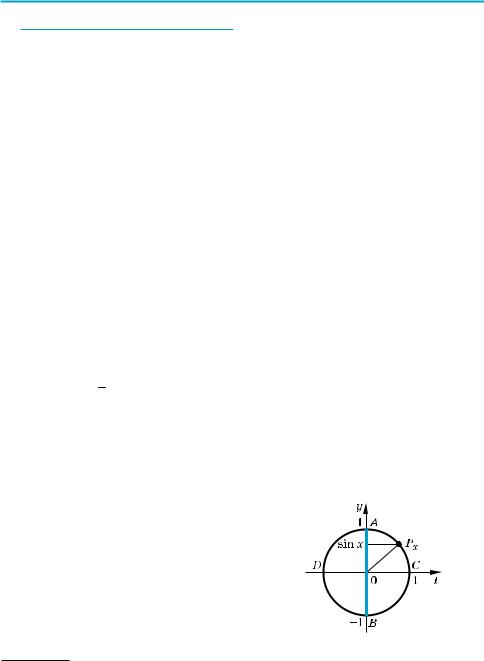
Нагадаємо, що значення синуса — це ордината відповідної точки одинич ного кола (рис. 51). Оскільки ординату можна знайти для будь якої точки одиничного кола, то область визначення функції y = sin x — усі дійсні числа. Це можна записати так: D (sin x) = R.
Для точок одиничного кола ординати набувають усіх значень від –1 до 1, отже, область значень функції y = sin x: y [–1; 1]. Це можна записати так:
E (sin x) = [–1; 1].
Як бачимо, найбільше значення функції sin x дорівнює одиниці. Це значен ня досягається тільки тоді, коли відповідною точкою одиничного кола є точ
ка A, тобто при x = π + 2πk, k Z.
2
Найменше значення функції sin x дорівнює мінус одиниці. Це значення досягається тільки тоді, коли відповідною точкою одиничного кола є точка B,
тобто при x = − π + 2πk, k Z.
2
Як було показано в § 4, синус — непарна функція: sin (–x) = –sin x, отже,
їїграфік симетричний відносно початку координат.
В§ 4 було обґрунтовано також, що синус — періодична функція з наймен шим додатним періодом T = 2π: sin (x + 2π) = sin x, отже, через проміжки довжиною 2π вигляд графіка функції sin x повторюється. Тому при побудові
графіка цієї функції досить побудувати графік на будь якому проміжку дов жиною 2π, а потім одержану лінію па
ралельно перенести праворуч і ліворуч уздовж осі Ox на відстані kT = 2πk,
де k — будь яке натуральне число. Щоб знайти точки перетину графі( ка функції з осями координат, згадає
мо, що на осі Oy значення x = 0. Тоді відповідне значення y = sin 0 = 0, тобто
графік функції y = sin x проходить че
рез початок координат.
Рис. 51
* Проміжки зростання і спадання функції інколи ще називають проміжками монотон ності функції.
57
РОЗДІЛ 1. Тригонометричні функції
На осі Ox значення y = 0. Отже, нам потрібні такі значення x, при яких sin x, тобто ордината відповідної точки одиничного кола, буде дорівнювати нулю. Це буде тільки тоді, коли відповідною точкою одиничного кола буде точка C або D, тобто при x = πk, k Z.
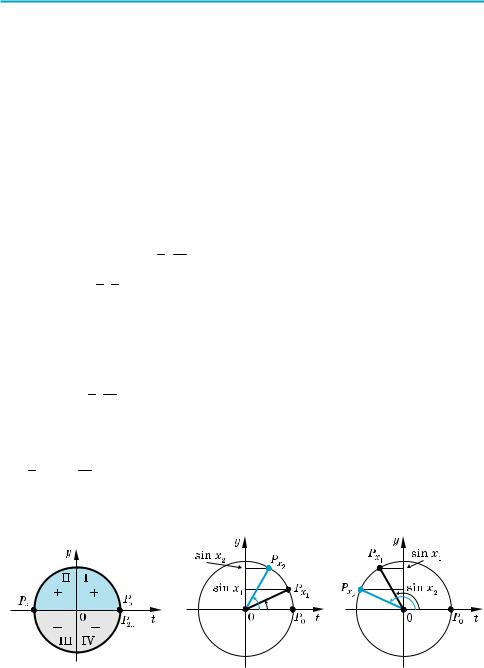
Проміжки знакосталості. Як було обґрунтовано в § 4, значення функції синус додатні (тобто ордината відповідної точки одиничного кола додатна) у I і II чвертях (рис. 52). Отже, sin x > 0 при x (0; π), а також, враховуючи період, при всіх x (2πk; π + 2πk), k Z.
Значення функції синус від’ємні (тобто ордината відповідної точки одинич ного кола від’ємна) у III і IV чвертях, отже, sin x < 0 при x (π + 2πk; 2π + 2πk), k Z.
Проміжки зростання і спадання.
(Враховуючи періодичність функції sin x з періодом T = 2π, досить досліди ти її на зростання і спадання на будь якому проміжку довжиною 2π, напри
клад, на проміжку −2π; 32π .
Якщо x −2π; 2π (рис. 53, а), то при збільшенні аргументу x (x2 > x1) орди
ната відповідної точки одиничного кола збільшується (тобто sin x2 > sin x1), отже, у цьому проміжку функція sin x зростає. Враховуючи періодичність, робимо висновок, що вона також зростає в кожному з проміжків
|
|
π |
|
π |
|
, k Z. |
|
|
− |
|
+2πk; |
|
+2πk |
||
2 |
2 |
||||||
|
|
|
|
|
Якщо x 2π; 32π (рис. 53, б), то при збільшенні аргументу x (x2 > x1) орди
ната відповідної точки одиничного кола зменшується (тобто sin x2 < sin x1), отже, у цьому проміжку функція sin x спадає. Враховуючи періодичність, робимо висновок, що вона також спадає в кожному з проміжків
π + 2πk; 3π + 2πk , k Z.)
2 |
2 |
|
Проведене дослідження дозволяє обґрунтовано побудувати графік функції y = sin x. Враховуючи періодичність цієї функції (з періодом 2π), досить спо
а |
б |
Рис. 52 |
Рис. 53 |
58
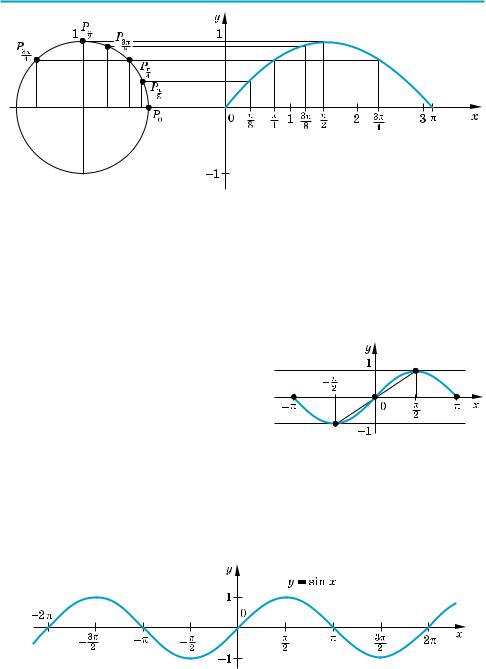
§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості |
Рис. 54 |
чатку побудувати графік на будь якому проміжку довжиною 2π, наприклад, |
||
на проміжку [–π; π]. Для більш точної побудови точок графіка користуємося |
||
тим, що значення синуса — це ордината відповідної точки одиничного кола. |
||
На рисунку 54 показана побудова графіка функції y = sin x на проміжку [0; π]. |
||
Враховуючи непарність функції sin x (її графік симетричний відносно початку |
||
координат), для побудови графіка на проміжку [–π; 0] відображуємо одержа |
||
ну криву симетрично відносно початку координат (рис. 55). |
||
Оскільки ми побудували графік на |
|
|
проміжку довжиною 2π, то, враховую |
|
|
чи періодичність синуса (з періодом 2π), |
|
|
повторюємо вид графіка на кожному |
|
|
проміжку довжиною 2π (тобто перено |
|
|
симо паралельно графік уздовж осі Ох |
|
|
на 2πk, де k — ціле число). |
|
|
Одержуємо графік, наведений на ри |
Рис. 55 |
|
сунку 56, який називається синусоїдою. |
||
|
||
З а у в а ж е н н я. Тригонометричні функції широко застосовуються в ма тематиці, фізиці та техниці. Наприклад, багато процесів, таких як коливан ня струни, маятника, напруги в колі змінного струму і т. п., описуються функ цією, яка задається формулою y = A sin (ωх + ϕ). Такі процеси називають гар( монічними коливаннями.
Рис. 56
59
РОЗДІЛ 1. Тригонометричні функції
Графік функції y = A sin (ωx + ϕ) можна одержати із синусоїди y = sin х стискуванням або розтягуванням її вздовж координатних осей і паралельним перенесенням уздовж осі Ох. Найчастіше гармонічне коливання є функцією часу t. Тоді воно задається формулою y = A sin (ωt + ϕ), де А — амплітуда коли
вання, ω — кутова частота, ϕ — початкова фаза, 2ωπ — період коливання.
5.2. ГРАФІК ФУНКЦІЇ y = cos x ТА ЇЇ ВЛАСТИВОСТІ
Т а б л и ц я 11
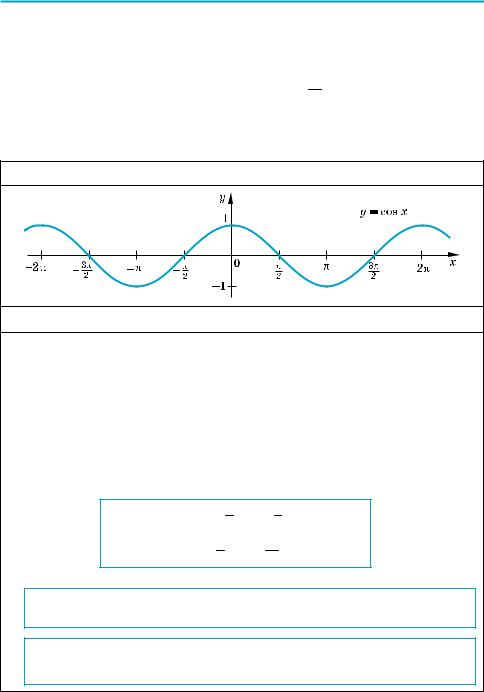
Графік функції y = cos x (косинусоїда)
Властивості функції y = cos x
1. |
Область визначення: x R ( x — будь яке дійсне число). |
D (cos x) = R |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Область значень: y [–1; 1]. |
E (cos x) = [–1; 1] |
|
|
|
|
|
|
|
||||
3. |
Функція парна: cos (–x) = cos x (графік симетричний відносно осі Oy). |
||||||||||||
|
|
|
|
|
cos (x + 2π) = cos x. |
||||||||
4. |
Функція періодична з періодом |
|
T = 2π |
: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
y = |
0, |
|||
|
|
|
|
|
x = 0, |
|
|
|
|
|
|
|
|
5. |
Точки перетину з осями координат: Оy |
|
|
Оx |
|
|
π |
|
|||||
|
|
|
|
|
y = 1 |
|
|
|
x = |
|
|
+ πk, k Z |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x > 0 при x (− 2π + 2πk; 2π + 2πk), k Z cos x < 0 при x (2π + 2πk; 32π + 2πk), k Z
7.Проміжки зростання і спадання:
функція cos x зростає на кожному з проміжків [π + 2πk; 2π + 2πk], k Z, і спадає на кожному з проміжків [2πk; π + 2πk], k Z.
8.Найбільше значення функції дорівнює 1 при x = 2πk, k Z. Найменше значення функції дорівнює –1 при x = π + 2πk, k Z.
60
