
OFP-Tretyak-Lozovski
.pdf
333 |
ДОДАТКИ |
Це однорідна система двох рівнянь із двома невідомими. Для існування нетривіальних розв'язків потрібно виконання умови занулення детермінанта системи. Звідси маємо
tgkwL / 2 =kb /kw . |
(H.7) |
Аналогічно для непарного розв'язку отримаємо умову
ctgkwL / 2 = −kb /kw . |
(H.8) |
Ці рівняння можна розв'язати чисельно, але наочніше – розв'язати їх графічно. Для цього перепишемо (H.7) і (H.8) у дещо іншому вигляді. А саме
|
|
|
(H.7) → tgkwL / 2 = |
|
|
V |
|
|
sin2ϕ |
|
V |
|
|
|
|
||||||
|
|
|
|
|
b −1; |
cos2ϕ |
= b −1; |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−cos2ϕ |
|
1 |
|
V |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
→ cosk |
|
L/2 = ± |
|
. |
|
|||||||||||
|
|
|
|
|
= |
|
−1 = |
b |
−1 |
w |
|
|
|||||||||
|
|
|
cos2ϕ |
cos2ϕ |
|
V |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
Це означає, що для tgkwL / 2> 0 мають виконуватись умови |
|
||||||||||||||||||||
|
|
|
|
|
|
coskwL / 2 = ±kw/k0 , |
|
|
|
|
|
|
(H.9) |
||||||||
де k |
|
|
|
|
|||||||||||||||||
0 |
= |
2m*V / 2 . У цьому рівнянні знак плюс вибирається для по- |
|||||||||||||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
зитивних значень coskwL / 2, а мінус – для негативних. |
|
|
|
|
|||||||||||||||||
Аналогічно можна записати й рівняння (H.8) |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
sinkwL / 2 = ±kw/k0 для ctgkwL / 2 < 0. |
|
|
|
(H.10) |
||||||||||||||
Тут знак плюс вибирається, |
якщо |
|
sinkwL / 2> 0 і |
мінус – |
якщо |
||||||||||||||||
sinkwL / 2 < 0. Ліві (L) та праві ( |
R) частини рівнянь (H.9) і (H.10) |
можна |
|||||||||||||||||||
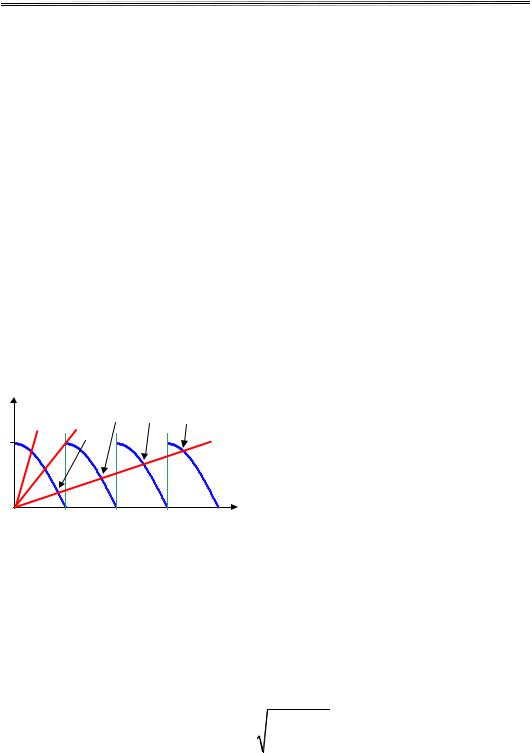
представити в одному графіку як функції величини kw. При цьому частини кривих в інтервалах
2π(l −1) |
< |
kw < |
2π(l −1/ 2) |
(H.11) |
|
L |
L |
||||
|
|
|
відповідають парним розв'язкам (тобто (H.9)), а частини кривих в інтервалах
2π(l −1/ 2) |
< |
kw < |
2πl |
(H.12) |
|
L |
L |
||||
|
|
|
– непарним розв'язкам (тобто (H.10)). Тут l = 1, 2, 3, … . Праві частини обох рівнянь є прямими лініями із кутовим коефіцієнтом k0−1, що










 z
z