
книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)
..pdf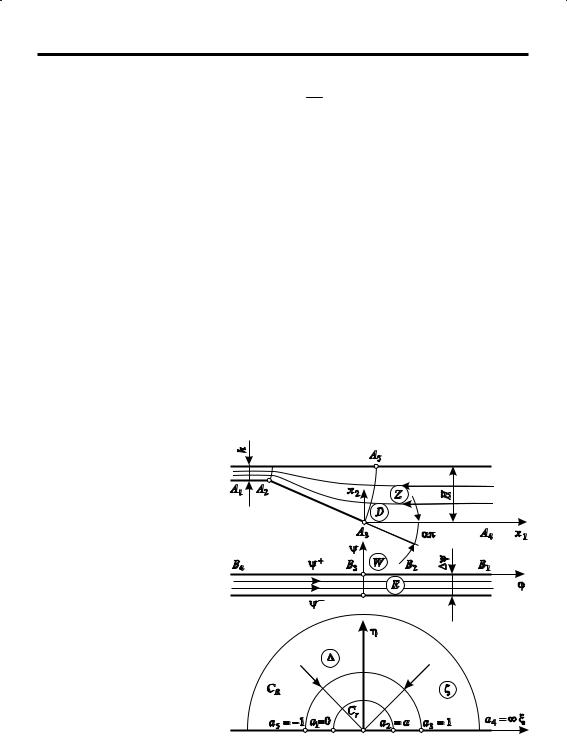
2.3. МЕТОДЫ ПОСТРОЕНИЯ НЕПРЕРЫВНЫХ КВ ПОЛЕЙ СКОРОСТЕЙ
[11 = –[22 = V0 h0 hc f ;
h2
|
|
|
|
|
h0 E1 |
§ |
2 |
|
2hc2 f 2 · |
|
||
[ |
12 |
= [ |
21 |
= V |
|
|
¨hcc f |
|
hc f |
|
¸ , |
(2.3.2) |
|
2 |
|
|
|||||||||
|
|
0 |
2h |
¨ |
|
|
h |
¸ |
|
|||
|
|
|
|
|
|
© |
|
|
¹ |
|
||
где текущая высота h вычисляется по формуле (П3.59), а ее первая и вторая производные – по формулам (П3.60) и (П3.64); производная склеивающей функции f (П3.61) вычисляется по формуле (П3.63).
Таким образом, во всей области : определены кинематические параметры (П3.58) и (2.3.2) процесса прокатки, которые с учетом (П3.57), (П3.59)–(П3.61), (П3.63) и (П3.64) непрерывно распределены в :. Эти кинематические параметры учитывают только геометрические характеристики очага деформации и могут быть использованы для оценки технологических параметров процесса плоской (без учета уширения полосы) прокатки. Для учета, кроме геометрических характеристик, реологии деформируемых металлов приведенное выше непрерывное поле скоростей (П3.58) следует рассматривать как основное в последующей корректировке.
2.3.2.Интеграл К. Шварца–Э. Кристоффеля
Вкачестве основного ре-
шения задач ОМД Г. Я. Гун предложил использовать гармонические поля скоростей, построенные с помощью интеграла К. Шварца–Э. Кристоффеля (П3.35). Необходимые элементы теоретических основ применения этого интеграла изложены в п. П3.1.4. Здесь использование интеграла К. Шварца–Э. Кристоффеля рассмотрим на примере течения сплошной среды в области, которую можно использовать для аппроксимации очага деформации при прессовании, волочении или прокатке (с заменой дуги захвата хордой) в условиях плоской деформации (рис. 85).
Рис. 85. Конформное отображение области D на плоскости W |
и ] для моделирования процесса прессования |
351
2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МЕХАНИКИ СПЛОШНЫХ СРЕД
Сначала выполним нормировку интеграла К. Шварца–Э. Кристоффеля для физической плоскости Z и плоскости W комплексного потенциала
для плоскости Z
k |
Ak |
ak |
αk |
1 |
– ∞ |
0 |
0 |
2 |
A2 |
a |
1 + α |
3 |
0 |
1 |
1 – α |
4 |
+ ∞ |
∞ |
0 |
|
|
|
|
для плоскости W
j |
Bj |
bj |
βj |
1 |
– ∞ |
0 |
0 |
2 |
B2 |
b |
1 |
3 |
0 |
1 |
1 |
4 |
+ ∞ |
∞ |
0 |
|
|
|
|
соответственно, где A2 = (H – h) [–ctg(απ)+i]. Тогда по формулам (П3.35) запишем интегралы, конформно отображающие обе плоскости на вспомогательную полуплоскость ζ:
ζ |
|
ζ − a |
α |
d ζ |
ζ |
d ζ |
|
|
|||
z (ζ) = c1 ∫ |
|
|
|
|
+ c2 ; w(ζ) = c3 ∫ |
|
+ c4 . |
(2.3.3) |
|||
ζ −1 |
ζ |
ζ |
|||||||||
ζ |
0 |
|
|
ζ |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Для обоих интегралов (2.3.3) назначим одинаковые нижние пределы интегрирования в точке ζ0 = 1 вспомогательной полуплоскости плоскости ζ. В физической плоскости Z образ этой точки находится в начале координат z = A3. Поэтому при ζ0 = 1 и при таком же верхнем пределе ζ = ζ0 имеем z(1) = c2 = 0. Тогда
ζ |
|
ζ − a |
α |
d ζ |
|
|
||
z (ζ) = c1 ∫ |
|
|
|
|
. |
(2.3.4) |
||
ζ −1 |
ζ |
|||||||
ζ |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
В плоскости W комплексного потенциала при ζ0 = 1 имеем w = 0 и при ζ = ζ0 имеем w(1) = c4 = iψ+ = 0. Тогда
w(ζ) = c |
lnζ + iψ+. |
(2.3.5) |
3 |
|
|
Если в плоскости ζ осуществить переход по окружности CR бесконечно большого радиуса R, то в плоскости Z ему будет соответствовать приращение
z = iH + 0 |
|
1 |
, где 0 |
|
1 |
– бесконечно малая величина порядка |
1 |
. Учиты- |
||
|
|
|
|
|
|
|
||||
|
|
R |
|
|
R |
|
R |
|
||
вая при этом переходе, что в подынтегральном выражении ζ >> 1 > a, из (2.3.4) имеем
352

2.3. МЕТОДЫ ПОСТРОЕНИЯ НЕПРЕРЫВНЫХ КВ ПОЛЕЙ СКОРОСТЕЙ
iH = c |
ζ |
d ζ |
. |
∫ |
|
||
1 |
ζ |
||
|
|
|
|
|
ζR |
|
|
Представим комплексную величину ζ в показательной форме ζ = ||ζ|| eiθ. Тогда dζ = ||ζ|| ieiθdθ, и последний интеграл представляется в виде
π
iH = c1 ∫id Ω = c1 i π .
0
Отсюда c1 = Hπ . Теперь точно так же рассмотрим переход по окружности Cr бес-
конечно малого радиуса r, которому соответствует приращение z = ih + 0(r), где 0(r) – бесконечно малая величина порядка r. Учитывая при втором переходе, что в подынтегральном выражении 1 >> a > ζ, из (2.3.4) имеем
iH = |
|
H |
∫ |
aα |
d ζ |
|
= iH α , |
|
|
|
||||||||||||
|
π |
|
|
|
|
|
|
|
||||||||||||||
|
|
Cr |
|
|
|
ζ |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a = |
α |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|||||||
Окончательно (2.3.4) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
h |
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
α |
|
|
|
|
||||||||||
|
H |
ζ |
|
ζ − |
|
|
|
|
d |
ζ |
|
|
||||||||||
|
|
|
|
|
||||||||||||||||||
z (ζ) = |
|
|
|
H |
|
|
|
|
||||||||||||||
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(2.3.6) |
||
|
π |
|
ζ −1 |
|
|
|
ζ |
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент c3 формулы (2.3.5) найдем, используя вспомогательную точку В5 = iψ–, симметричную точке В3 (рис. 85). Так как образу точки В3 в плоскости ζ соответствует b3 = 1 (см. нормировку), то образом точки В5 в этой же плоскости является b5 = –1. Тогда при ζ = 1 и w = iψ– из (2.3.5) имеем
iψ– = c3iπ + iψ+.
353

2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МЕХАНИКИ СПЛОШНЫХ СРЕД
Поскольку Δψ= ψ+ – ψ–, то c3 = − Δψπ . Окончательно получим формулу, аналогичную (П3.36):
w(z) = − |
Δψ lnζ. |
(2.3.7) |
|
π |
|
Формулы (2.3.6) и (2.3.7) в параметрическом виде z = z(ζ); w = w(ζ) определяют комплексный потенциал w = w(z). Также в параметрической форме можно определить вектор скорости, который является комплексно сопряженной величиной первой производной w по z (П3.29): V = w′ .
Упражнение 2.2.8. Используя (2.3.6) и (2.3.7), показать, что комплексная скорость имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζ −1 |
|
|
|
|
|
|||
W ′ = |
dw |
= − |
Δψ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
(2.3.8) |
||
dz |
H |
|
|
|
|
|
1 |
|
|||||
|
|
|
|
h |
|
|
|
|
|||||
|
|
ζ − |
α |
|
|||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
H |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
2.3.3.Суперпозиция гармонических течений
Вп. П3.1.5 изложены теоретические основы суперпозиции гармонических течений. Здесь в качестве примера рассмотрим применение этого метода для построения плоского, непрерывного КВ-поля скоростей, которое можно использовать как основное решение в последующей корректировке при моделировании процесса прокатки металла в абсолютно жестких валках (их упругая деформация пренебрежимо мала) в условиях плоской деформации.
Прежде всего выполним анализ течения металла при листовой прокатке в плос-
кости x1 x2, когда уширение металла в направлении x3 пренебрежимо мало. В этом случае деформация металла будет плоской. Предположим, что заготовка в виде
прямоугольного параллелепипеда с размерами h0b0  0 движется поступательно с постоянной скоростью в сторону вращающихся валков. Если бы зазор h1 между рабочими валками был больше высоты h0 или равен ей, то заготовка, попадая в область вращающихся валков, продолжала бы участвовать в поступательном движении с постоянной скоростью (тензоры дисторции и скорости дисторции равны нулю). Если же на пути движущейся заготовки встречаются вращающиеся валки с
0 движется поступательно с постоянной скоростью в сторону вращающихся валков. Если бы зазор h1 между рабочими валками был больше высоты h0 или равен ей, то заготовка, попадая в область вращающихся валков, продолжала бы участвовать в поступательном движении с постоянной скоростью (тензоры дисторции и скорости дисторции равны нулю). Если же на пути движущейся заготовки встречаются вращающиеся валки с
354
2.3. МЕТОДЫ ПОСТРОЕНИЯ НЕПРЕРЫВНЫХ КВ ПОЛЕЙ СКОРОСТЕЙ |
|
зазором между ними h1 < h0, то про- |
|
исходит деформация прокатывае- |
|
мого металла, т. е. валки будут ис- |
|
точником возмущения однородно- |
|
го потока металла со скоростью V0 |
|
(вектор дисторции dU отличен от |
|
нуля). При этом после выхода из |
|
зазора между валками металл опять |
|
будет участвовать в однородном по- |
|
токе, но с другой скоростью vf. |
|
Для имитации этого процесса с |
|
помощью гармонических полей |
|
скоростей рассмотрим суперпози- |
|
цию двух течений: бесчисленного |
|
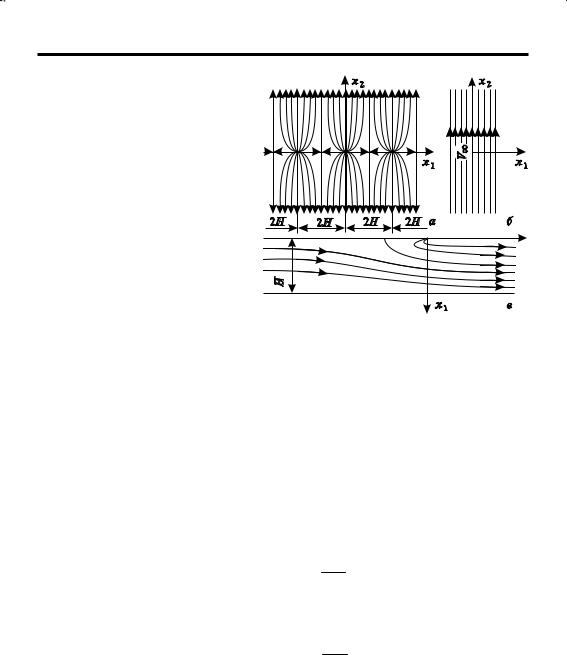
множества источников (рис. 86) |
Рис. 86. Множество источников (а), однородный по9 |
одинаковой интенсивности >0, |
ток (б) и их суперпозиция (в) |
|
|
находящихся на действительной |
|
оси х1 на одинаковом расстоянии 2Н друг от друга, с комплексным потенциалом |
|
(П3.45), и однородного потока в направлении оси х2 с комплексным потенциалом |
|
(П3.41) при C0 = –iVφ, где Vφ – скорость набегающего на источники однородного |
|
потока. Суммарный комплексный потенциал нового течения будет иметь вид |
|
w |
'\ |
Insin |
Sz |
iV z. |
(2.3.9) |
|
|
||||
|
2S |
2H |
φ |
|
|
|
|
|
|||
Разложением w(z) на действительную Μ и мнимую части (П3.11) найдем консервативную функцию
M |
|
'\ |
ª |
Sx2 |
cos |
||||
|
|
|
ln «ch |
|
|
||||
|
4S |
2H |
|||||||
|
|
|
¬ |
|
|
||||
и функцию тока |
|
|
|
|
|
|
|
|
|
\ |
|
'\ |
|
§ |
|
Sx |
|||
|
|
|
arctg¨ctg |
|
1 |
th |
|||
|
2S |
|
|
||||||
|
|
|
© |
|
2H |
||||
Sx1 º» Vφ x2
2 H ¼
Sx2 ·¸ Vφ x1 .
2H ¹
(2.3.10)
(2.3.11)
Далее, дифференцируя комплексный потенциал (2.3.9) по z, найдем комплексную скорость (П3.15)
c '\ |
|
Sz |
iVφ , |
|
||
w |
|
ctg |
|
(2.3.12) |
||
4S |
2H |
|||||
|
|
|
|
|||
355

2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МЕХАНИКИ СПЛОШНЫХ СРЕД
комплексно сопряженная величина которой равна вектору скорости V (П3.29).
Разложением V на мнимую и действительную части определяем компоненты вектора скорости:
V1 = Δψ |
|
sin |
πx1 |
|
|
= Δψ |
|
sh |
πx2 |
|
|
|
|
H |
|
; V |
|
H |
|
+V . (2.3.13) |
|||||
|
|
|
|
|
|
|
|
|
||||
4π ch |
πx2 |
− cos |
2 |
4π ch |
πx2 |
− cos |
|
∞ |
||||
πx1 |
πx1 |
|||||||||||
|
|
H |
|
|
H |
|
|
H |
|
H |
||
При x1 = ±H имеем V1 = 0. Поэтому линии x1 = ±H являются линиями тока, вдоль которых вектор скорости имеет только одну компоненту, отличную от нуля:
|
|
Δψ |
sh |
πx2 |
||
V2 |
= |
H |
|
+V∞ . |
||
4π ch πx2 |
|
|||||
|
|
+1 |
||||
|
|
|
|
H |
|
|
Причем если ImV∞ = 0 и V∞ ≠ 0, то вдоль этих линий везде V2 ≠ 0. Из анализа функций V1 и V2 (2.3.13) следует, что линия x1 = 0 является линией симметрии течения. На этой линии V1 = 0, а
|
|
Δψ |
sh |
πx2 |
||
V2 |
= |
H |
|
+V∞ . |
||
4π ch πx2 |
|
|||||
|
|
−1 |
||||
|
|
|
|
H |
|
|
Отсюда ясно, что точка x1 = 0; x2 = 0 является сингулярной и, кроме того, на линии x1 = 0 имеется точка бифуркации x2 = хб, где V2 = 0. Подстановкой этого условия в последнюю формулу находим мнимый аффикс такой точки:
xб = Hπ ln λ1 ,
где
V∞ + Δψ
λ = 4 H .
V∞ − 4ΔψH
356

2.3. МЕТОДЫ ПОСТРОЕНИЯ НЕПРЕРЫВНЫХ КВ ПОЛЕЙ СКОРОСТЕЙ
При x2 = –∞ компоненты вектора скорости (2.3.13) имеют значения V1 = 0 и
V2 |
= V0, где V0 |
= − |
Δψ |
+V∞ , а при x2 = +∞ компоненты вектора скорости V1 = 0 и |
|||||
|
|
|
|
4π |
|
|
|
|
|
V |
= V , где V |
f |
= Δψ |
+V . Отсюда, учитывая обозначение параметра λ, нахо- |
|||||
2 |
f |
|
4π |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дим, что Vf = λV0 и Δψ = 4HV0c1; V∞ = V0 c2, где |
|
|
|||||||
|
|
|
|
|
c = λ −1; |
c = λ +1. |
(2.3.14) |
||
|
|
|
|
|
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
||
С учетом полученных значений Δψ и V∞ кинематические параметры (2.3.10), (2.3.11), (2.3.13) имеют следующий вид:
консервативная функция
|
ϕ = |
V0 Hc1 |
|
ln |
ch πx2 − cos |
πx1 |
|
+V c |
x ; |
|
|
(2.3.15) |
|||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
π |
|
|
|
2 H |
2 H |
|
|
|
0 2 |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
функция тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ = |
V0 Hc1 |
arctg |
ctg πx1 th |
πx2 |
|
−V c |
x ; |
|
|
(2.3.16) |
||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
π |
|
|
|
2 H |
2 H |
|
0 2 |
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
компоненты вектора скорости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
πx1 |
|
|
|
|
|
|
|
|
sh |
πx2 |
|
|
|
|
|||
V1 =V0c1 |
|
sin H |
|
|
; |
V2 =V0c1 |
|
|
|
H |
|
|
|
+V0c2 . |
(2.3.17) |
||||||
ch |
πx |
πx |
ch |
πx |
− cos |
πx |
|||||||||||||||
|
|
|
2 − cos |
|
1 |
|
|
|
|
|
2 |
H |
1 |
|
|||||||
|
|
H |
|
H |
|
|
|
|
|
H |
|
|
|
|
|
||||||
Из анализа компонент вектора скорости следует, что общее направление потока однородного течения до и после возмущения его источниками не меняется. Значит, величина потока Q1 =2V0H при x2 = –∞ должна быть равна потоку Q2 = 2Vfh, где 2h – ширина потока при x2 = +∞. Учитывая соотношение между V0 и Vf, из равенства потоков Q1 и Q2 находим
λ = |
H |
. |
(2.3.18) |
|
|||
|
h |
|
|
357

2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МЕХАНИКИ СПЛОШНЫХ СРЕД
Таким образом, λ есть коэффициент уменьшения высоты однородного потока в результате обтекания им источника в области 0 ≤ х1 ≤ H.
Покажем, что построенное поле скоростей (2.3.17) можно использовать при моделировании процесса плоской прокатки.
Сначала рассмотрим значение функции тока (2.3.16) на произвольной линии тока в точке с координатами х1 = H – D; x2 = – ∞. Учитывая, что c1 – c2 = –1 (2.3.14), имеем
ψ |
x2 =−∞ |
= −V0 (Hc2 − D). |
(2.3.19) |
|
x1=H −D |
|
|
Легко показать, что эта же линия тока при x2 = – ∞ становится тоже прямой линией, параллельной оси x2. Обозначим уровень этой линии при x2 = – ∞ через х1 = H – d. Тогда, учитывая, что c1 + c2 = λ (2.3.14), находим
ψ |
x2 =+∞ = −V0 (Hc2 − λd ). |
(2.3.20) |
|
x1=H −d |
|
В связи с тем, что вдоль одной и той же линии тока имеем ψ = const, приравнивая (2.3.19) и (2.3.20), получим
λ = |
D |
. |
(2.3.21) |
|
|||
|
d |
|
|
Таким образом, показано, что параметр λ равен отношению исходной высоты канала, в котором движется поток, к его конечной высоте. В теории ОМД этот параметр при плоской деформации несжимаемой среды называется коэффици
ентом вытяжки.
Уравнение x2 = x2 (x1) произвольной линии тока, проходящей через точку с координатами х1 = H – D; x2 = – ∞, найдем из совместного решения (2.3.16) и (2.3.19) с учетом (2.3.21):
|
|
|
cos |
π(Hc2 − D− x1 ) |
|
||||
x2 = |
H |
2 Hc1 |
|
|
|
|
|||
|
|
|
|
|
|
||||
π |
ln |
|
π(λd − Hc + x λ) |
. |
(2.3.22) |
||||
|
|
|
cos |
|
2 |
1 |
|
|
|
|
|
|
|
2 Hc1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для того чтобы связать полученное поле скоростей (2.3.17) с процессом прокатки металла, необходимо параметрам обтекания источников в полосе шириной 2Н однородным потоком поставить в соответствие технологические параметры процесса прокатки. Частично это проделано выше. Действительно, скорость V∞ набегающего однородного потока и мощность источников Δψ мы
358

2.3. МЕТОДЫ ПОСТРОЕНИЯ НЕПРЕРЫВНЫХ КВ ПОЛЕЙ СКОРОСТЕЙ
выразили через величину V0, которая для процесса прокатки интерпретируется как скорость входа металла в валки, и нашли связь параметров c1 и c2 по формулам (2.3.14) с коэффициентом вытяжки λ.
В формулах (2.3.19)–(2.3.22) введем обозначения D = h20 и d = h21 , где в соответ-
ствии с теорией прокатки h0 – высота заготовки, а h1 – высота готового проката. Теперь единственным непонятным, с точки зрения теории прокатки, параметром является ширина Н полосы, в которой осуществляется обтекание источника однородным потоком. Из теории прокатки известно, что параметры геометрического очага деформации определяются высотой заготовки h0, высотой готового проката h1 и радиусом рабочего валка R. Так как параметр Н также определяет картину течения, то, очевидно, этот параметр должен зависеть от всех перечисленных геометрических параметров процесса прокатки.Эту зависимость, например, можно определить, если совместить центр валка со средневзвешенным центром кривизны граничной линии тока в области наибольшего возмущения однородного потока источником в полосе шириной 2Н. Однако такая процедура затруднительна как при безмашинном определении координат центра кривизны, так и при расчете их на ЭВМ. Наиболее просто и приемлемо дляпрактических расчетов координаты центра валкаможно найти, если центр кривизны граничной линии тока определять в точке пересечения этой линии с осью абсцисс х1. Тогда подстановкой в (2.3.22) значения ординаты x2 = 0 на оси абсциссы найдем координату х1 = H – r точки пересечения, где
r = |
h0 h1 |
. |
(2.3.23) |
|
|
||||
|
h + h |
|
||
|
0 |
1 |
|
|
В точке х1 = H – r; x2 = 0 вычислим радиус кривизны граничной линии тока, которая контактирует с рабочим валком, и приравняем его радиусу валка:
|
|
dx2 |
|
2 |
32 |
|
|
|
|
|
|
|
|||
|
1 |
+ |
dx |
|
|
|
|
|
|
|
|
|
|
||
R = |
|
1 |
|
|
, |
||
|
|
d 2 x |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
dx12
где, как результат дифференцирования (2.3.22), имеем
dx |
|
c |
|
πr |
d 2 x |
|
c |
|
πc |
|
|
|
|
||
2 |
|
2 |
|
|
|
2 |
|
2 |
|
2 |
|
|
|
(2.3.24) |
|
dx |
= c |
ctg 2 H ; |
dx2 |
= c |
2 H c sin |
2 |
π r . |
||||||||
|
|
||||||||||||||
1 |
1 |
|
|
|
1 |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 H |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
359
2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МЕХАНИКИ СПЛОШНЫХ СРЕД
Подстановкой этих производных в предыдущую формулу получим
R |
H c2 |
|
2 |
Sr § |
c22 |
2 |
Sr ·3 2 |
|
|||
|
sin |
|
|
¨1 |
|
ctg |
|
|
¸ . |
(2.3.25) |
|
Sc1 |
|
|
|
|
|
||||||
|
|
|
2 H ¨ |
c2 |
|
2 H ¸ |
|
||||
|
|
|
|
© |
1 |
|
|
¹ |
|
||
Теперь найдем координаты xc, yc центра кривизны граничной линии тока в точках х1 = H ρ r; x2 = 0, куда поместим центры рабочих валков:
|
|
|
|
dx2 |
ª |
§ |
dx2 |
·2 º½ |
|
|
|
|
|
§ dx2 |
· |
2 |
|
|
||||||
|
|
° |
|
«1 ¨ |
¸ |
»° |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
° |
|
dx |
« |
© |
|
dx |
¹ |
» |
° |
|
|
|
1 ¨ |
dx |
¸ |
|
|
|
||||
x |
H r |
° |
r |
1 |
¬ |
|
|
1 |
¼ |
° |
|
y |
|
|
© |
¹ |
. |
|
||||||
® |
|
|
|
|
|
|
¾ |
; |
c |
|
1 |
|
(2.3.26) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
c |
|
|
|
|
d2 x2 |
|
|
|
|
|
|
|
d2 x2 |
|
|
|
|
|||||||
|
|
° |
|
|
|
|
|
|
° |
|
|
|
|
|
|
|
|
|
||||||
|
|
° |
|
|
|
2 |
|
|
|
° |
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
° |
|
|
|
dx1 |
|
|
|
|
° |
|
|
|
|
|
dx1 |
|
|
|
|
|||
|
|
¯ |
|
|
|
|
|
|
|
|
|
¿ |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь знаку «+» соответствуют координаты нижнего валка, а знаку «–» – верхнего. Подстановкой в (2.3.26) производных (2.3.24) находим:
|
|
ª |
|
H |
|
|
Sr |
§ |
|
|
2 |
|
|
Sr |
·º |
|||||||
x |
|
H r «r |
sin |
|
¨1 |
c2 |
ctg2 |
¸»; |
||||||||||||||
|
|
|
|
|
|
c2 |
|
|
||||||||||||||
c |
|
« |
|
2S 2 H ¨ |
|
|
|
2 H ¸ |
» |
|||||||||||||
|
|
¬ |
|
|
|
|
|
|
|
© |
|
|
1 |
|
|
|
|
¹¼ |
||||
y |
|
|
2 H c |
2 |
sin2 |
Sr § |
c2 |
|
ctg2 |
Sr · |
|
|
||||||||||
|
|
|
|
|
|
¨1+ |
2 |
|
|
¸. |
(2.3.27) |
|||||||||||
|
|
Sc1 |
|
2 H |
c2 |
|
|
|||||||||||||||
|
c |
|
|
|
|
|
¨ |
|
|
|
2 H ¸ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
© |
1 |
|
|
|
¹ |
|
|
||||
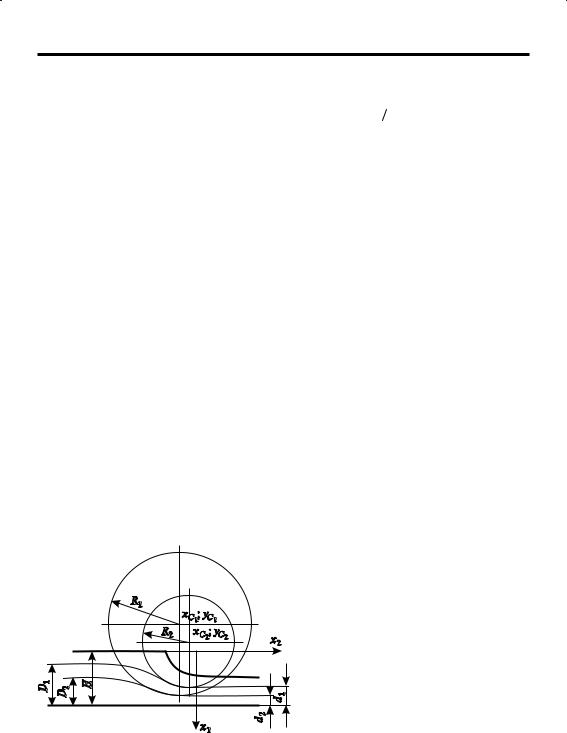
С помощью формул (2.3.22) и (2.3.27) построены варианты областей с различными коэффициентами
вытяжки (2.3.18) и радиусами валков
(2.3.25), соответствующие процес-
сам прокатки (рис. 87).
Из теории прокатки известны
безразмерные параметры, определяю-
щие процесс прокатки с геометри-
ческой точки зрения. К таким пара-
метрам относятся:
– относительная деформация
Рис. 87. Изменение области течения металла при прокатке в зависимости от масштабного фактора H
360
