книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

271

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

пропорциональную расстоянию между плоскостью двойникования и рассматриваемой атомной плоскостью (рис. 64). При этом ребра кристаллической решетки, наклоненные сначала к плоскости двойникования под углом , после двойникования поворачиваются на

кристаллографическим плоскостям, которые называются плоскостями сколь жения. Обычно такими плоскостями являются плоскости с наибольшей плотностью размещения атомов. В этих плоскостях имеются направления, в которых меж-атомные расстояния имеют минимальную величину. Такие направления называются направлениями скольжения. В совокупности плоскости и направления образуют структуру скольжения*. Например, в металлах с решеткой типа К12 (табл. 1) структуру скольжения обычно образуют плоскости типа (111) и направления типа [101]; в металлах с решеткой типа Г6 эту структуру могут образовывать плоскости типа (0001) и направления типа [2 1 10]; в металлах с решеткой типа К8 – плоскости типа (110) и направления типа [111] (рис. 48). Параметры структур скольжения могут зависеть от температуры. Так, при комнатной температуре для металлов с решеткой типа Г12 структура скольжения включает плоскости типа (0001), а при температуре, превышающей 480 K, появляется дополнительная возможность скольжения в плоскостях типа (1011) или (1012).

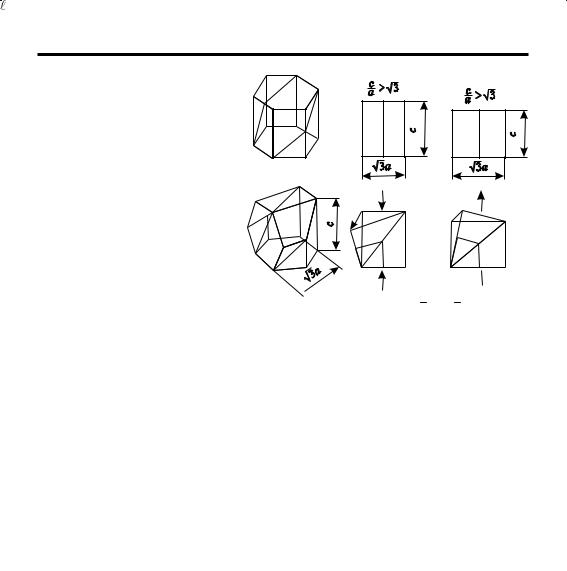
Решетка части кристалла, участвующей в пластической деформации за счет двойникования, является как бы зеркальным отражением недеформированной части кристалла относительно плоскости двойникования. Плоскости двойникования обычно совпадают с плоскостями скольжения. Двойникование сравнительно редко наблюдается при статическом нагружении и значительно чаще – при деформировании ударом. Этот способ пластической деформации наиболее характерен для металлов с решеткой типа Г12 (рис. 65).

При скольжении у металлов значения пределов текучести при испытаниях на растяжение и сжатие почти одинаковы, так как этот способ пластической деформации практически инвариантен к направлению приложенной силы.

При двойниковании значения пределов текучести одного и того же металла существенно зависят от знака приложенной нагрузки: плюс при растяжении и

*Ранее применявшийся термин «система скольжения» не соответствует понятию «система».

272

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

минус при сжатии. Это объясняется тем, что двойникование

может происходить лишь при определенном направлении прикладываемого усилия, а при обратном – отсутствовать. Например, пределы текучести магния при растяжении и сжа-

тии могут отличаться в два раза. Другой причиной анизотро-

пии свойств деформированных металлов является неодинако-

вость пластической деформа- ции в различных направлениях Рис. 65. Схемы двойникования (1012) [1011] в металлах

деформируемого объема. Такой тип анизотропии будем назы-

вать деформационным. Он проявляется не только в моно-, но и в поликристаллических телах. Так, неодинаковость деформации удлинения и уширения при листовой прокатке металла приводит к соответствующей анизотропии свойств прокатанной продукции.

1.5.9. Оценка эффективных свойств сплошных композитных сред

Прежде чем приступить к изложению различных концепций оценки эффективных свойств гетерогенных материалов, рассмотрим решение одной из простейших задач механики сплошных композитных сред, имеющее для дальнейшего изложения важное методическое значение.

ной 2h1 (–h1 δ E2 δ h1) под действием постоянного во времени перепада давления р = p1 – p2 (для определенности считаем p1 > p2) на длине движется в направлении оси E1 многослойная линейно-вязкая, изотропная, несжимаемая среда с определяющим уравнением (1.5.35) в каждом i-м слое. Кроме того, предполагается, что среда каждого слоя является однородной. Требуется определить параметры НДС (тензоры напряжений Tς, скоростей деформаций T[) в области движения многослойной среды (рис. 66).

Математическая постановка задачи. Сначала запишем замкнутое множество уравнений относительно неизвестных параметров движения среды. В качестве исходного используем уравнение (1.5.37). В нем для плоского течения в плоскости E1E2 принимаем L3 = E3. Тогда, исключая в (1.5.37) среднее напряжение

273

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Рис. 66. К решению задачи о движении в прямолинейной полосе многослойной линейно9вязкой среды (I, II, III … – область движения сред с одинаковыми свойствами)

ς0, для линейно-вязкой среды при функции состояния Π* = const из (1.5.41) без учета массовых и инерционных сил получаем, что функция тока < должна быть бигармонической (П2.62):

т.е. имеем одно дифференциальное уравнение с одной неизвестной величиной.

Всвязи с тем, что область течения симметрична относительно оси E1, а среда в каждом i-м слое изотропна и однородна, движение в этой области должно быть

направлено по линии действия приложенных сил (по оси E1). Иными словами, линии тока в такой области должны быть параллельны оси E1, и в соответствии с (1.2.105) функция тока будет зависеть только от одной координаты E2. Поэтому (1.5.108) представляется в виде

В связи с тем, что по условию задачи течение среды является стационарным для искомых параметров течения, запись краевых условий сводится к записи лишь граничных условий.

Для замкнутого относительно < множества (1.5.109) кинематические граничные условия запишем в скоростях, учитывая свойство линейно-вязкой среды прилипать к границам:

274

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

где Sмсi – межслойная линия тока i- и i +1-го слоев. Статические граничные

условия заданы только на левой и правой границах области движения многослойной среды (рис. 66):

Ниже будет показано, что кинематические граничные условия (1.5.110) позволяют найти поле скоростей с точностью до константы, которая определяется интегрированием уравнения равновесия с помощью статических граничных условий (1.5.111).

Таким образом, на верхней и нижней границах области течения среды (рис. 66) и на межслойных линиях тока заданы кинематические граничные условия, а на левой и правой границах – смешанные граничные условия. Теперь можно приступить к решению поставленной краевой задачи.

Решение задачи. Уравнение (1.5.109) легко интегрируется, и с учетом граничных условий (1.5.110) с помощью (1.2.105) находим компоненты вектора скорости

где h0 = h1; j ≤ i – 1.

Константы ai определим путем интегрирования уравнения равновесия (1.4.18) с учетом статических граничных условий (1.5.111). По формуле Дж. Стокса (1.2.137) поле скоростей (1.5.112) позволяет определить компоненты тензора скоростей деформаций для i-го слоя

i

которые, в свою очередь, с помощью определяющего уравнения (1.5.35) позволяют рассчитать компоненты девиатора напряжений

275

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

где μ*i – коэффициент вязкости i-й среды. В связи с тем, что диагональные компоненты девиатора напряжений s11i = −s22i = 0, для тензора напряжений имеем

σ11i = −σi22 = σi0. Теперь, с учетом последнего соотношения в (1.5.114) из (1.4.18),

используя граничные условия (1.5.111), находим константы интегрирования уравнения (1.5.109)

и компоненты тензора напряжений в области движения многослойной среды

Таким образом, получили точное решение (1.5.116) и (1.5.118) задачи о движении многослойной линейно-вязкой среды в прямолинейной полосе под действием перепада давления p.

Если в расчетной схеме (рис. 66) принять h1 = h и hi = 0 при i > 1, то получим, как частный вариант, известное в гидромеханике решение аналогичной задачи о движении во всей области однородной линейно-вязкой среды, для которой

μ*i = μ*. В этом случае единственная отличная от нуля константа интегрирования уравнения (1.5.109) a1 = а имеет вид

276

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

Соответствующим образом изменятся компоненты вектора скорости

а напряжения (1.5.116) останутся в том же виде. Последнее означает, что в рассматриваемом случае любая аппроксимация свойств линейно-вязкой среды для получения точных значений компонент тензора напряжений эффективна, так

как при любых значениях коэффициентов вязкости μ*i , в том числе и при замене многослойного течения однородным течением (μ*i = μ* ), в результате решения задачи имеем точные значения напряжений в виде (1.5.116).

Теперь потребуем сохранения потока среды при замене многослойного течения с коэффициентом вязкости μ*i каждого слоя течением однородной среды с эффективной в этом смысле вязкостью μ*эфф. Для многослойного течения такой поток равен сумме потоков каждого из слоев, которые получим с помощью компонент вектора скорости (1.5.117). Удельное значение такого потока,

Аналогичный поток однородной среды с эффективными свойствами получим с помощью поля скоростей (1.5.120), где вместо μ* нужно подставить μ*эфф :

Приравнивая (1.5.122) и (1.5.123), находим

277

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Упражнение 1.5.15. С помощью (1.5.118) и (1.5.121) показать, что эффективные свойства однородной среды, при течении которой средняя по сечению полосы скорость деформации совпадает со средней в этой же полосе скоростью деформации многослойного течения, определяются функцией состояния

При реализации некоторых проблем удобно использовать усредненные по объему свойства композитной среды. В рассматриваемом случае такое усреднение необходимо провести по высоте полосы:

Критерием получения эффективных свойств гомогенной среды вместо свойств гетерогенной может служить равенство энергетических затрат при движении обеих сред при прочих равных условиях.

Таким образом, при замене гетерогенных сред гомогенными эффективность свойств последних определяется критерием замены. Так, если в рассмотренной задаче критерием замены является равенство потоков многослойной и однородной сред, то эффективные свойства однородной среды определяются соотношениями (1.5.122), (1.5.124); при выдвижении в качестве критерия равенства средних скоростей деформаций – соотношением (1.5.125) и т. п.

Среды с эффективными в том или ином смысле свойствами называются эф фективными модулями. В некоторых случаях удается краевой задаче МСС с определяющими соотношениями композитной среды поставить в соответствие такую же краевую задачу МСС с определяющими соотношениями эффективного модуля. Теория, основанная на определении свойств однородной среды путем решения такой задачи, называется теорией эффективного модуля. Чаще всего такая теория применима для сред с несложными свойствами упругих, вязких композитов. На основании теории эффективного модуля, в результате решения двух указанных краевых задач МСС, в области движения композитной среды можно рас-

278

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

сматривать движение однородной среды с «размазанными», как назвал их Б. Е. Победря, свойствами. При этом предполагается совпадение осредненных по объему энергетических потенциалов:

для упругопластичных сред

Приведенная выше задача о движении линейно-вязкой среды позволяет с помощью (1.5.116) и (1.5.118) рассчитать потенциал (1.5.130) для i-го слоя композитной среды:

а с помощью (1.5.116) и (1.5.121) – для эффективного модуля:

Подстановкой (1.5.131) и (1.5.132) в (1.5.129), на основании теории эффективного модуля имеем:

279

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

где hN+1 = 0.

Так же, как и ранее (1.5.124)–(1.5.126), эффективные свойства (1.5.133) позволяют в частном случае получить точное значение напряжений (1.5.116), но они не дают достоверной информации о характере распределения кинематических параметров. В более общих случаях теория эффективного модуля не позволяет оценить достоверность расчета параметров НДС. Однако можно показать, что с помощью энергетических потенциалов удается произвести оценку области изменения характеристик эффективных модулей, внутри которой находится точное решение. Границы такой области называют «вилкой».

Для приближенного определения эффективных характеристик гетерогенных сред, кроме приведенного, существует много других энергетических методов. К ним, в частности, относятся принцип Дж. Д. Эшелби, двусторонние оценки по методу В. Фойгта–А. Рейсса или по методу З. Хашина–С. Штрикмана и др. Два последних метода связаны с применением вариационных принципов МСС и будут рассмотрены ниже.

Сущность принципа Дж.Д. Эшелби состоит в замене интегрирования по объему при вычислении энергии деформирования упругих сред интегрированием по поверхности. Предположим, что сплошная среда M = Mα Mβ состоит из матрицы (окружения) Mα и включения Mβ, а параметрами НДС при упругом деформировании этого тела являются тензор напряжений Tσ и тензор дефор-

маций Tε.

Определим энергию внутренних сил деформирования гетерогенного тела с учетом соотношения (1.4.50):

Если же эту область будет занимать только среда окружения Mα, то при прочих равных условиях параметрами НДС будут тензоры Tσ0 и Tε0 , в общем случае отличные от тензоров Tσ и Tε. Тогда энергия внутренних сил будет иметь вид

Вычитанием (1.5.135) из (1.5.134) получим:

280