
Диссертация на соискание учёной степени
.pdf
P |
(t) |
Pelect (t) |
, |
|
||
|
|
|
||||
1 2 |
|
|
Pelect (t) Ptun |
(t) Pinact (t) |
|
|
|
|
|
|
|
||
P |
(t) |
|
Ptun |
(t) |
, |
(2.35) |
|
|
|
||||
1 3 |
|
|
Pelect (t) Ptun |
(t) Pinact (t) |
|
|
|
|
|
|
|
||
P |
(t) |
Pinact (t) |
. |
|
||
|
|
|
||||
1 4 |
|
|
Pelect (t) Ptun |
(t) Pinact (t) |
|
|
|
|
|
|
|
||
В данной работе предполагается, что при осуществлении быстрых переходов не происходит изменения конформационной координаты по уравнению Ланжевена. Медленная конформационная динамика в течение промежутка времени t реализуется только в отсутствии быстрых переходов.
На основе сделанных предположений была получена марковская цепь,
которая реализовывалась с помощью метода Монте-Карло. В рамках этого метода нормально распределенная случайная величина 1 задается на i-том шаге реализации процесса в момент времени ti i t на отрезке [0,1] и
сравнивается с вычисленной вероятностью электронных переходов между ветвями КП. Если выполняется условие 1 P1 2 , реализуется электронный переход между ветвями КП. В ином случае определялась следующая случайная величина 2 , которая сравнивалась с условной вероятностью туннельного перехода. По аналогии с предыдущим случаем, если 2 P1 3 , то реализуется туннельный переход, в другом случае определяется случайная величина 3 .
При 3 P1 4 моделируется инактивационный переход, в противном случае вычисляется конформационная координата на текущем шаге по уравнению Ланжевена.
Повторяя описанную процедуру T t раз, где Т – длительность эксперимента, и вычисляя конформационную динамику на отрезках [t j , t j 1 ], на которых отсутствуют переходы, можно получить одну реализацию случайного процесса, которая является приближением исходного марковского процесса электронных и туннельных переходов.
71
2.3.3 Численная схема для ЭК-модели RyR-канала
Объединяя методы Эйлера-Марайамы для реализации конформационной динамики, метод марковских цепей и метод Монте-Карло для реализации туннельных и электронных переходов, была получена численная схема для реализации электронно-конформационной модели рианодинового канала,
которая выглядит следующим образом:
1. |
Отрезок времени [0,T] разбивается на N равных промежутков |
|
длительностью t . |
|
|
2. |
Задание начальных условий при t 0 : |
0 0 , 0 (0) , Q0 Q(0) , |
q0 q(0) ; |
|
|
3.Задание счетчика цикла i 0.
4.Начало цикла по i 1, N .
5.Для каждого i 1, N определение случайных величин i ,
подчиненных нормальному распределению с математическим ожиданием,
равным нулю, и дисперсией, равной 1;
6.Получение случайного числа i [0,1] , подчиненное равномерному
распределению на этом отрезке;
7.Если i =0:
7.1Вычисление вероятности электронного перехода Pelect elect (Qi , i , i ) t ;
7.2Вычисление вероятности туннельного перехода Ptun tun (Qi , i , i ) t ;
7.3Если i Ptun Pelect , то
i 1 i ;
Qi 1 Qi qi t ;
|
|
|
K |
|
|
p |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
qi 1 qi |
|
|
Qi |
qi |
|
|
|
0 i |
1 i |
|
t V i |
t ; |
||
M |
M |
2M |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Переход к (10);
7.4Определение случайного числа 1 [0,1], подчиненное равномерному
распределению на этом отрезке;
72

7.5 Если 1 |
|
|
Pelect |
, то |
|
Pelect |
Ptun Pinact |
||||
|
|
|
Qi 1 Qi ,
i 1 ( i 1) mod 2
Переход к (10).
7.6 Если 1 |
|
|
Pelect |
, то i 1 |
i , иначе: |
|
Pelect |
Ptun Pinact |
|||||
|
|
|
|
7.7 Определение случайного числа 2 [0,1] , подчиненное равномерному распределению на этом отрезке;
7.8 Если 2
7.9 Если 2
|
|
Ptun |
|
, то Qi 1 |
||
Pelect |
Ptun |
Pinact |
||||
|
|
|
||||
|
если i 0 , то Qi 1 |
QO |
||||
|
если i 1 , то Qi 1 |
QO |
||||
|
i 1 |
( i |
1) mod 2 |
|
||
|
Переход к (10) |
|
|
|||
|
|
Ptun |
|
, то |
|
|
P |
P |
P |
|
|||
|
elect |
tun |
inact |
|
|
|
Qi , иначе:
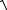
 QO2 hz 2E(Qi , i , i ) ;
QO2 hz 2E(Qi , i , i ) ;
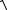
 QC2 hz 2E(Qi , i , i ) ;
QC2 hz 2E(Qi , i , i ) ;
7.9.1 Определение случайного числа 3 [0,1] , подчиненное равномерному распределению на этом отрезке;
7.9.2 Если 3 |
|
|
Pinact |
, то |
|
Pelect Ptun Pinact |
|||||
|
|
|
|||
|
Qi 1 |
Qi , i 1 i и i 1 ( i 1) mod 2 |
|||
Переход к (10).
8.Если i =1:
8.1 Определение случайного числа |
3 [0,1] , |
подчиненное равномерному |
||||
распределению на этом отрезке; |
|
|
|
|||
8.2 Если 3 |
|
Pinact |
, то Qi 1 |
Qi , i 1 |
i и i 1 ( i 1) mod 2 |
|
Pelect |
Ptun Pinact |
|||||
|
|
|
|
|||
73
9.Изменение счетчика цикла i : i 1;
10.Если i t T , то переход к (4), иначе вычисление закончено.
В результате реализации численной схемы формируются векторы
Qi , qi , i , i , i 0,1,..., N , являющиеся приближениями решения начальной задачи для ЭК-модели в моменты времени ti i t .
Система обыкновенных дифференциальных уравнений (2.28), описывающая зависимости концентраций Са2+ в отделах кардиомиоцитов от времени решалась в данной работе с помощью обыкновенного метода Эйлера, причем концентрации в каждом из отделов определялись в каждый момент времени i 1, N .
Преимуществом данной схемы численной реализации является ее универсальность. Схема подразумевает возможность изменения вида конформационного потенциала и упрощение в связи с пренебрежением некоторыми переходами на больших интервалах времени.
2.4 Описание программного комплекса
Для численных экспериментов на базе модели высвобождающей единицы с интегрированной в нее ЭК моделью динамики RyR-каналов были разработаны алгоритмы, позволяющие производить расчет при различных условиях экспериментов и различных наборах параметров. Эти алгоритмы реализованы в виде комплекса программ, состоящего из двух частей. Первая часть является расчетно-демонстрационной, вторая предназначена для обработки результатов численных экспериментов.
Первая часть представляет собой вычислительную систему, ядро которой реализовано в программной среде Borland C++ Builder 6 (рис. 2.16) и является большим программным комплексом с удобными для пользователя интерфейсом и аппаратом управления моделируемыми процессами.
Особенностью, разработанного в данной диссертационной работе,
программного комплекса является его многозадачность. Этот комплекс
74

называется ReleaseUnit.exe и при определенном выборе опций в программе позволяет независимо проводить следующие эксперименты:
Моделирование динамики статистического ансамбля изолированных RyR-каналов (9х9) при фиксированном уровне Са2+ в
рамках ЭК теории.
При проведении данного типа экспериментов в программе исследуются кинетические характеристики RyR-каналов при различных параметрах ЭК-
модели. В программе осуществляется усреднение по ансамблю таких кинетических характеристик, как вероятность пребывания канала в открытом состоянии, времена пребывания в открытом и закрытом состояниях и др.
Моделирование динамики кластера взаимодействующих RyR-
каналов (9х9) при фиксированном уровне Са2+ в рамках ЭК теории.
В данном классе экспериментов исследуется влияние взаимодействия между
RyR-каналами на кинетические характеристики всего кластера.
Моделирование динамики ионов Са2+ между компартментами высвобождающей единицы, включая влияние соответствующих буферов,
в рамках модели ВЕ с учетом стохастической динамики кластера RyR-
каналов.
Рис. 2.16. Скриншот программного комплекса ReleaseUnit.exe, разработанного для проведения численных экспериментов в рамках ЭК-модели и модели ВЕ.
75

Частично обработка и аппроксимации результатов экспериментов проводились во второй части комплекса программ, реализованных в системе
Wolfram Mathematica 5.0-8.0 (рис. 2.17), пакете символьной математики с огромными возможностями вычислений и обработки данных.
Первичный параметрический анализ модели и апробация численных методов для оптимального решения уравнений модели проводились в данной среде. Однако в связи с большими затратами времени для расчетов среда
Wolfram Mathematica не удовлетворяла потребностям при решении поставленных задач при проведении длительных экспериментов (10-15 мин для
20000 итераций для каждого набора параметров модели).
Рис. 2.17. Общий вид среды Mathematica 8.0. В левом окне продемонстрирована аппроксимация результатов численных экспериментов по исследованию активности изолированных RyR-каналов точным решением уравнения Колмогорова. Справа – расчет интенсивностей электронных переходов в ЭК-модели.
Программный комплекс включает в себя более десяти программ,
позволяющих решить задачи численного моделирования и обработать результаты экспериментов.
2.5 Заключение
Дан краткий обзор электронно-конформационной модели RyR-канала,
предложенной ранее в работах [A2, A3, 93, 94].
76
В развитие модели дан детальный анализ различных параметров и факторов, влияющих на динамику канала, таких как концентрация Са2+ в cis и trans-частях вблизи канала и кооперативная динамика кластера RyR-каналов.
Впервые в ЭК-модели предложено введение инактивационного состояния, соответствующего взаимодействию ионов Са2+ с инактивационными центрами RyR-канала.
Впервые в рамках электронно-конформационной теории предложена модель взаимодействия ионов Са2+ с активационным центром RyR-канала,
учитывающая вероятности заполнения мест присоединения активационного центра ионами Са2+.
Дана детализация модели туннельных переходов, включающая введение
«зоны разрешенного туннельного перехода» вблизи минимума конформационного потенциала RyR-канала.
ЭК-модель кластера RyR-каналов объединена с моделью Са2+-
высвобождающей единицы с целью детального изучения работы внутренних Са2+-«часов» в клетках водителя сердечного ритма на макромолекулярном уровне.
Разработан многоцелевой компьютерный комплекс, реализующий алгоритмы численного решения уравнений электронно-конформационной модели, на базе которого проводились серии экспериментов, результаты которых представлены в главах 3 и 4 данной работы.
77
ГЛАВА 3. Результаты численного моделирования. Активность одиночного RyR-канала при стационарных условиях
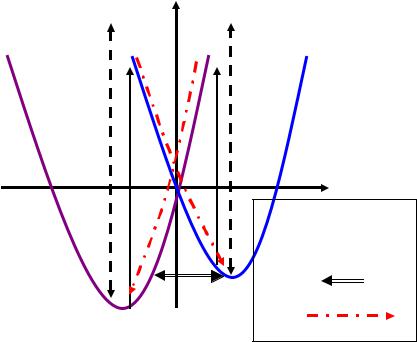
Моделирование динамики RyR-канала проводилось в рамках схемы,
представленной на рисунке 3.1. Данная схема предполагает наличие трех энергетических уровней (E+, E-, I), двух типов переходов между ними и медленной конформационной динамики к минимумам конформационного потенциала.
E(Q)
|
|
I |
|
E+(Q) |
|||
E-(Q) |
|||
|
|
||
Q
Электронные переходы
E+  E-
E-
I  E+,-
E+,-
Туннельные переходы
O |
E+ |
E- |
Конформационные переходы |
||
C
Рис. 3.1. Схема динамики одиночного RyR-канала.
В ходе проведения численных экспериментов изучались зависимости конформационной координаты Q RyR-канала от времени при постоянном значении cis[Ca] для различных значений основных параметров ЭК модели
(рис. 3.2).
Варьирование параметров модели меняет характер динамики RyR-канала.
Как видно из графиков, коэффициент упругости канала К влияет на максимальное и минимальное значения конформационной координаты Q.
Параметр эффективного трения Г влияет на скорость релаксации RyR-канала к
78

локальному минимуму КП. Видно, что при достаточно малых значениях Г наблюдается колебательный характер динамики RyR-канала вблизи конформационного минимума, а при достаточно больших Г колебаний вблизи минимума не наблюдается.
В ЭК модели, согласно формуле (2.10), вероятность электронных переходов зависит от концентрации Са2+ в cis-части, в связи с этим, при изменении cis[Ca]
меняется частота переходов канала из одного состояния в другое и длительность пребывания в открытом и закрытом состояниях.
Подробно влияние параметров модели на характер динамики RyR-канала рассмотрено в данной работе далее (см. п.п. 3.2.1, 3.2.2).
а.
Q(t)
б.
Q(t)
в.
Q(t)
|
|
|
|
K=8 |
|
|
|
|
K=10 |
|
|
|
|
K=12 |
|
|||
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мМ |
0.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=7 cis[Ca]=0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г=2 |
|
|
|
|
|
Г=7 |
|
|
|
|
Г=15 |
|
||
0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мМ |
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K=12 |
cis[Ca]=0.1 |
-0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
-0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
cis[Ca]=0.5 мкМ |
|
|
|
cis[Ca]=5 мкМ |
|
|
|
cis[Ca]=50 мкМ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K=12 |
=7 |
-0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
-0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
200 |
400 |
600 |
800 |
1000 |
0 |
200 |
400 |
600 |
800 |
1000 |
0 |
200 |
400 |
600 |
800 |
1000 |
|
|
|
t, мс |
|
|
|
|
t, мс |
|
|
|
|
t, мс |
|
|
|
|||
Рис. 3.2. Зависимости конформационной координаты RyR-канала от времени, результаты численных экспериментов; а. при различных значениях коэффициента упругости К; б. при различных значениях коэффициента эффективного трения Г; в. при различных значениях концентрации цитозольного кальция cis[Са2+].
3.1 Анализ временных зависимостей конформационной координаты Q
При проведении численных экспериментов исследовалась динамика одиночного RyR-канала. В начальный момент времени канал находился в электронно- и конформационно-закрытом состоянии. Результаты
79

экспериментов по изучению зависимости конформационной координаты Q
от времени обрабатывались с помощью метода нормированного размаха
(R/S-анализ или метод Херста) [43, 116].
Этот метод позволяет выявить скоррелированность определенного ряда данных на больших интервалах времени и определить фрактальную
размерность временного ряда – размерность Хаусдорфа-Безиковича:
D 2 H , где Н – показатель Херста.
Согласно [116], значения Н>0.5 указывают на положительную
корреляцию (персистентный процесс), а Н<0.5 на отрицательную
корреляцию (антиперсистентный процесс) измеряемой величины со временем. И тот и другой процессы являются процессами с «памятью»,
когда последующие события определяются предшествующими. Величина Н=0.5 характеризует случайный процесс.
Среднее значение координаты Q на промежутке времени τ определяется
как:
|
|
|
1 |
|
|
|
Q |
|
Q(t) , |
(3.1) |
|||
|
||||||
|
|
t 0 |
|
|||
где t – дискретное время с шагом dt. В данной работе dt выбиралось равным
0.05 c, длительность эксперимента: =1 с. |
|
|
|
|
Накопившееся |
отклонение конформационной координаты |
|
от |
среднего |
|
t |
|
. |
|
значения Q(t) |
определяется как: X (t, ) Q(u) Q(t) |
|
Разность |
|
|
u 1 |
|
|
|
|
|
|
|
|
между максимальным и минимальным значениями Q(t) в выборке
(кумулятивное отклонение от среднего) на интервале времени τ описывается формулой:
R( ) max X (t, ) min X (t, ) , |
(3.2) |
|
1 t |
1 t |
|
Стандартное отклонение Q(t) от :
1
S Q(t)
t 1
Q(t) |
|
2 |
1/2 |
|
|
|
. |
(3.3) |
|
|
|
|
|
|
|
|
|
|
80
