
Диссертация на соискание учёной степени
.pdf2.2.1 Электронно-конформационная модель решетки RyR-каналов
2.2.1.1 Гамильтониан решетки RyR-каналов
Кластер RyR-каналов на мембране СР в высвобождающей единице представляется как квадратная решетка RyR-каналов с общим числом каналов до 100, каждый из которых описывается электронно-конформационной моделью одиночного RyR-канала.
В данной работе рассмотрение сопряжения каналов в кластере ограничивалось приближением, учитывающим взаимодействия только ближайших соседних каналов с «упругой» константой взаимодействия Kmn . С
учетом этих условий гамильтониан канала с номером m в решетке может быть представлен в виде:
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
H |
m |
h s |
h s |
xm |
pQ |
aQ s |
K Q2 |
1 |
|
K |
(Q Q )2 |
(2.17), |
|
|
z zm |
x |
m |
m zm |
|
m |
|
|
mn |
m n |
|
||
m,n
где sxm , szm – матрицы Паули; m и n – номер канала в решетке (каналы пронумерованы от 1 до 81). При этом предполагается, что конформационные взаимодействия испытывают только соседние RyR-каналы, поэтому если m и n – номера ближайших соседей, то Kmn k , и Kmn 0 в остальных случаях.
Две ветви конформационного потенциала каждого канала решетки
определяется формулой:
E (Qm ) K Qm2 |
pQm 1 |
|
1 |
k(Qm Qn )2 . (2.18) |
|
[(hz aQm )2 |
hx2 ]2 |
||||
2 |
2 |
|
|
|
n |
Для частного диабатического случая ( при 0 , |
h 0 ) конформационный |
||||
потенциал (2.5) с учетом взаимодействия в приближении ближайших соседей принимает вид:
E (Qm ) K Qm2 |
pQm 1 aQm k(Qm Qn )2 . |
(2.19) |
|
2 |
2 |
n |
|
Как и в случае изолированного канала (2.5), конформационный потенциал в диабатическом случае имеет форму двух пересекающихся парабол.
2.2.1.2 Влияние концентрации Са2+ в люмене на вид конформационного
потенциала RyR-канала
61
При рассмотрении влияния ионов Са2+ на канал со стороны trans-части в модели изолированных RyR-каналов введен параметр эффективного давления p
(2.6). Можно провести аналогию между уровнем trans[Ca] в липидном бислое in vitro и значением концентрации Са2+ в люмене СР (CajSR ) in vivo:
p 2 |
(Ca |
jSR |
)n |
1, |
(2.20) |
||
|
|
|
|
||||
(Ca |
jSR |
)n K n |
|||||
|
|
|
|
Ca |
|
|
|
где KCa – уровень CajSR , при котором параметр p имеет нулевое значение, n –
коэффициент Хилла. Параметр эффективного давления, как отмечалось ранее,
лежит в интервале: p [ 1;1] . В терминах уровня заполнения люмена ионами Са2+ значение p 1 соответствует минимальному, а р=1 – максимальному заполнению люмена.
Как уже отмечалось в предыдущей главе, эффективное давление является одним из важнейших параметров, определяющих форму конформационного потенциала и устойчивость того или иного состояния RyR-канала.
2.2.2 Схема динамики RyR-каналов в решетке высвобождающей единицы
Для моделирования динамики RyR-каналов в решетке высвобождающей единицы можно пренебречь существованием инактивационного состояния,
подробно описанного во второй главе данной работы, в связи с тем, что характерные времена работы внутриклеточных Са2+-«часов» малы по сравнению с характерными временами перехода RyR-канала в инактивационное состояние [24]. В дальнейшем использована простейшая схема открытия/закрытия RyR-каналов в процессе заполнения/высвобождения Са2+.
62

оC |
E(Q) |
|
сO |
||
|
||
|
2 |
|
1 |
|
|
|
Q |
3 |
оO |
|
|
сC |
|
Рис. 2.12. Простейшая схема динамики RyR-канала в ЭКмодели.
Данная схема (рис. 2.12) включает в себя процессы электронной активации (стрелка 1), медленную конформационную динамику (стрелка 2) и,
наконец, туннелирование из метастабильного состояния в глобальный
максимум (стрелка 3).
Для упрощения в формуле вероятности электронных переходов (2.8) предполагалось , так что Pelect elect (CaSS ) и не зависит от энергии ионов
Ca2 . Зависимость вероятности электронной активации от концентрации
полагалась “пороговой”:
|
|
max |
/ ( CaSS ), |
при CaSS |
CaSS crit |
|
|
|
elect |
electCaSS |
, |
(2.21) |
|||||
(CaSS ) |
|
|
CaSS crit |
|
|
|||
|
0, при CaSS |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
где electmax – амплитуда вероятности электронных переходов, α – параметр,
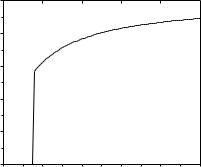
CaSS crit – некоторое критическое значение уровня CaSS . Для наглядности зависимость elect (CaSS ) приведена на рисунке 2.13.
63
|
0.010 |
|
|
|
|
|
Рис. |
|
2.13. |
|
Зависимость |
||
|
|
|
|
|
|
|
|
|
|||||
|
0.008 |
|
|
|
|
|
вероятности |
|
|
электронных |
|||
|
|
|
|
|
|
переходов |
от |
|
концентрации |
||||
|
|
|
|
|
|
|
|
||||||
|
0.006 |
|
|
|
|
|
Са2+ |
в диадном |
пространстве |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
elect |
|
|
|
|
|
|
при max =0.01, α = 1.2·10-6 М, |
||||||
|
|
|
|
|
|
|
|
elect |
|
|
|
||
|
0.004 |
|
|
|
|
|
Ca |
|
|
=1.5·10-6 |
М. |
||
|
|
|
|
|
|
SS crit |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0.002 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
-6 |
6 |
8 |
10 |
|
|
|
|
|
|
|
|
|
Ca |
, 10 |
M |
|
|
|
|
|
|
|
|
|
|
|
SS |
|
|
|
|
|
|
|
|
|
|
2.2.3 Сопряжение динамики RyR-каналов с динамикой кальция в |
|||||||||||||
отделах высвобождающей единицы |
|
|
|
|
|
|
|||||||
Для создания замкнутой модели высвобождающей единицы с учетом стохастической динамики RyR-каналов была установлена связь между параметрами теории высвобождающей единицы и ЭК-моделью.
В модели высвобождающей единицы поток высвобождающегося Са2+ в
диадное пространство зависит от числа открытых каналов в кластере.
|
81 |
|
|
|
|
|
Nopen i , |
|
(2.22) |
||
|
i 1 |
|
|
|
|
|
|
при 1 и |
Q Q |
|
|
где |
1, |
– значение |
|||
i |
i |
i |
C – «открытость» канала, где QC |
||
|
0, |
иначе |
|
|
|
|
|
|
|
|
|
конформационной координаты точки локального максимума нижней ветви C
конформационного потенциала (3.3.3) (см. рис. 2.3).
Таким образом, динамика концентрации кальция в отделах высвобождающей единицы вызывает изменение параметра p , который влияет на динамику состояний RyR-каналов, и как следствие, на число открытых RyR-
каналов Nopen. Переменная Nopen, в свою очередь, определяет скорость высвобождения кальция из люмена СР.
На основе вышеизложенных положений получена замкнутая объединенная модель, на базе которой в данной работе проводилось численное моделирование динамики Са2+ в отделах кардиомиоцитов.
64
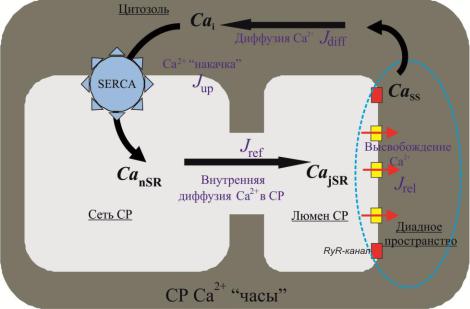
2.2.4 Модель Са2+-высвобождающей единицы
Разработка модели Са2+-высвобождающей единицы основана на широко известной модели структуры клетки (рисунок 2.14) [90, 112, 113], состоящей из четырех основных компонентов: диадного пространства, цитозоля, сети СР и просвета ТЦ (люмена) СР. Особенностью данного представления является рассмотрение обобщенной Са2+ высвобождающей единицы.
Рис. 2.14 Схема кальциевых токов между компонентами Са2+-«часов».
Основываясь на схеме динамики Са2+ в клетке, введены четыре кальциевых
потока между отделами клетки: |
|
|
|
|
|
1. |
Поток заполнения люмена J refill |
(от англ. refill – заполнять), его значение |
|||
зависит от параметра скорости заполнения k |
refill |
и разности концентраций Са2+ |
в |
||
|
|
|
|
|
|
сети СР и в люмене и определяется как: |
|
|
|
||
Jrefill krefill (CanSR CajSR ) . |
|
|
(2.23) |
|
|
2. |
Поток высвобождения Са2+ |
из люмена J rel (от англ. release |
– |
||
высвобождать), величина которого зависит от числа открытых каналов в
кластере высвобождающей единицы Nopen |
и от величины потока Са2+ через |
одиночный открытый канал jrel : |
|
Jrel Nopen jrel . |
(2.24) |
65
Значение потока Са2+ через одиночный канал определяется формулой: |
|
|||||
j k |
rel |
(Ca |
jSR |
Ca ), |
(2.25) |
|
rel |
|
SS |
|
|
||
где krel – параметр скорости высвобождения, CajSR |
– концентрация Са2+ |
в |
||||
люмене, |
Ca |
– концентрация Са2+ в диадном пространстве. |
|
|||
|
|
SS |
|
|
|
|
3. Диффузионный поток между диадным пространством и цитозолем Jdiff |
, |
|||||
значение которого зависит от градиента концентраций Са2+ в диадном пространстве и в цитозоли (Cai ) и определяется как:
Jdiff kdiff (CaSS Cai ) , |
(2.26) |
где kdiff – параметр скорости диффузии. |
|
4. Поток заполнения сети СР J up (от англ. |
uptake – накачка). Процесс |
накачки СР кальцием против градиента концентрации требует энергетических затрат (фосфорилляция молекул АТФ), значение потока зависит от концентрации Са2+ в цитозоле и от параметров Са2+-насоса: kup (скорость накачки) и Kup (чувствительность насоса). Для зависимости потока от концентрации Са2+ была использована формула, заимствованная из модели [54]:
(2.27)
Кальциевые потоки в упрощенной модели сердечной клетки (рис. 2.14) с
учётом квазистационарного взаимодействия с кальциевыми буферами
описываются стандартной системой дифференциальных уравнений [91]:
dCanSR |
knSRi |
Jup Jrefill ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dCajSR |
|
|
|
|
|
|
CQtot KdCQ |
|
|
1 |
k nSR J |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
J |
|
; |
|
|
||||||||||||||||||||||||
|
|
(Ca |
|
|
|
K |
|
|
|
|
|
refill |
|
|
(2.28) |
|||||||||||||||||||||
dt |
|
|
|
|
|
|
|
jSR |
dCQ |
)2 |
|
jSR |
|
|
|
|
rel |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dCaSS |
|
|
|
|
|
|
CM tot KdCM |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
k jSR J |
|
|
J |
|
|
|
; |
|
|
|
|
||||||||||||||||||||
|
|
|
)2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
dt |
|
|
|
|
|
|
(Ca |
|
K |
dCM |
|
|
SS |
|
rel |
|
|
diff |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
SS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dCai |
|
|
|
|
TCtot KdTC |
|
|
|
|
|
CM tot KdCM |
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
kSSJ |
diff |
Jup |
, |
|||||||||||||||||||||||
dt |
|
|
)2 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
(Ca K |
dTC |
|
|
(Ca K |
dCM |
)2 |
|
|
i |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В модели учитывается связывание ионов Са2+ с регуляторными глобулярными белками – буферами, которые участвуют в процессе мышечного
66
сокращения. Были учтены следующие Са2+-связывающие буферы,
содержащиеся в кардиомиоците: кальсеквестрин, кальмодулин, тропонин.
Параметры концентраций буферов, учитывающиеся в модели, взяты из работы [85]: CQtot = 10-2 М полная концентрация кальсеквестрина, CMtot = 45·10-6 М полная концентрация кальмодулина, TCtot = 31·10-6 М - полная
концентрация тропонина C. k |
константы отношений объемов |
и |
отделов |
|||||
|
|
|
|
|
|
|
|
|
клетки (рис. 2.14) ( ki |
= 40, |
knSR = 9.7, |
k jSR = 0.12, kSS = 0.022). |
K |
= 833·10- |
|||
nSR |
|
|
jSR |
SS |
i |
|
dCQ |
|
6 M, KdCM = 2.4·10-6 M, |
|
KdTC = |
5·10-6 M – |
константы |
|
диссоциации |
||
соответствующих буферов. Следует отметить, что все эти параметры выбраны как типичные для интегративной модели, а не для модели одиночной высвобождающей единицы.
Другими словами, было предположено, что все RyR-каналы формируют систему идентичных высвобождающих единиц, функционирующих согласованно. Параметры ЭК модели (2.5, 2.7, 2.8) при проведении численных экспериментов имели следующие значения: a = 5, K = 12, hx 0 , Г = 7.
Параметры туннелирования: A = 1, tun = 0.01 [A2].
2.3 Методы численной реализации модели
Электронно-конформационное состояние RyR-канала описывается стохастическим дифференциальным уравнением (2.7) со случайным изменением правой части и с переключением вследствие электронных и туннельных переходов (2.8, 2.10).
В формулах (2.4, 2.5) переменная электронного состояния является дискретной и принимает два значения: 0 (электронно закрытое) и 1 (электронно отрытое состояние). Слагаемое temp в уравнении (2.7) отвечает за аддитивные шумы в виде случайного винеровского процесса. Таким образом, компьютерная реализация ЭК модели должна быть основана на численных методах интегрирования стохастических дифференциальных уравнений и методах
67

реализации марковских процессов. Сочетание этих методов позволило построить две численные схемы для получения наборов реализаций.
2.3.1 Метод Эйлера-Марайамы
Наиболее известным методом решения дифференциальных уравнений со
случайными членами является явный метод Эйлера, обобщенный для стохастических уравнений Марайамой (Maruyama) в 1955 году, поэтому этот метод иногда называют методом Эйлера-Марайамы [114, 115].
Стохастическое дифференциальное уравнение Ито, описывающее изменение
со временем некоторой переменной X t , имеет вид [115]:
dX t a( X t )dt b( X t )dWt , |
(2.29) |
Пусть оно задано на интервале времени [0; T] с начальными условиями |
|
X (0) X 0 , где a( X t ) и b( X t ) |
– измеримые функции, а Wt отвечает за |
винеровский процесс. Данный интервал времени можно дискретизировать с
шагом |
t T |
, где L – число шагов на выбранном интервале. Дискретный |
||
|
|
L |
|
|
набор |
моментов времени на интервале обозначается как: |
ti i t , X i – |
||
приближенное решение уравнения (2.29) на каждом i-ом шаге. |
|
|||
Согласно схеме Эйлера-Марайамы решение на последующем шаге |
||||
находится как: |
|
|
||
X i 1 |
X i |
a( X i ) t b( X i ) Wi , |
(2.30) |
|
где Wi |
W (ti 1 ) W (ti ) – приращение винеровского процесса, для которого |
|||
справедливо соотношение [115]: |
|
|||
W (ti 1 ) W (ti ) ~ 
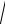 ti 1 ti
ti 1 ti 
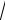 t ,
t ,
где – нормально распределенная случайная величина с нулевым средним и единичной дисперсией. С учетом этого схема метода принимает вид:
Xi 1 Xi |
a( Xi ) t b( Xi ) |
|
t i |
где i |
- нормально |
распределенная случайная величина (N(0,1)), |
|
вычисленная методом Монте Карло на i-ом шаге интегрирования системы уравнений.
68

Если обозначить скорость изменения координаты Q как q dQdt , то для
уравнения Ланжевена (2.7) в ЭК-модели, описывающего изменение конформационной координаты RyR-канала, метод Эйлера-Марайамы имеет вид:
|
|
Qi |
qi t, |
|
|
|
|
|
|
|||||
Qi 1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.31) |
|
|
|
|
|
|
1 E(Qi , i ) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
q |
q |
q |
t t |
. |
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|||||||||||
i 1 |
i |
|
M Q |
i |
|
|
i |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
2.3.2 Реализация электронных и туннельных переходов. Метод Монте-
Карло
Электронные и туннельные переходы в ЭК-модели можно представить в терминах дискретного марковского процесса с различными вероятностями переходов между состояниями марковской цепи. Для описания случайных марковских процессов обычно используют метод Монте-Карло, который заключается в применении генератора псевдослучайных чисел для моделирования случайного процесса переходов между состояниями.
Простейшим способом описания инактивационного состояния является введение новой переменной μ, принимающей два значения: μ=1, если канал инактивирован, μ=0 в остальных случаях. Если ввести функцию Хэвисайда
1, |
при 1 |
то с учетом новой |
переменной |
адиабатический |
||||||
( ) 0, |
при 0 , |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
конформационный потенциал (2.4) имеет следующей вид: |
|
|||||||||
E(Q, , ) ( ) I |
|
|
|
|
||||||
|
|
|
|
|
1 |
, |
(2.32) |
|||
(1 ) |
K |
Q2 |
pQ ( 1) |
1 |
[( aQ)2 |
h2 ] |
2 |
|
|
|
|
|
|
||||||||
|
2 |
2 |
|
|
|
|
|
|||
где I – энергия инактивационного состояния.
Диабатический конформационный потенциал (2.5) может быть описан следующей формулой:
69
K |
Q2 pQ ( 1) |
1 |
|
|
|
E(Q, , ) ( ) I (1 ) |
|
|
aQ . |
(2.33) |
|
|
|
||||
|
2 |
|
2 |
|
|
Для инактивационного состояния, была введена новая переменная μ.
Рассмотрим состояние канала 1: Q, , в определенный момент времени t .
В следующий момент времени t t система может оказаться в состояниях 2:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Q, , |
|
или 3: |
Q, , |
|
или 4: |
Q, , |
|
(рис. 2.15). |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 Q, , |
|
|
|
|
|
Рис. 2.15. Схема случайных |
|||||||
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
переходов |
из |
текущего |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
состояния. |
Стрелки: |
1 |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электронная |
активация, |
2 |
– |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 Q, , |
|
|
3 Q, , |
|
|
4 Q, , |
туннелирование, |
3 |
|
– |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электронная инактивация. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предполагается, что потоки событий электронных и туннельных переходов между состояниями являются пуассоновскими. Опираясь на это предположение, дискретизируем марковский процесс с таким малым шагом по времени t , что за этот промежуток времени может произойти только одно событие перехода.
На каждом шаге интегрирования случайного процесса вероятности туннельного, электронного перехода между ветвями КП и вероятность перехода в инактивационное состояние определялись следующим образом:
Ptun (t) tun (Q(t)) t,
Pelect (t) elect (Q(t)) t, |
(3.34) |
Pinact (t) inact (Q(t)) t. |
|
Так как события туннельных и электронных переходов являются независимыми, то вероятность покинуть состояние 1 за время t равна
Pel (t) Ptun (t) Pinact (t) .
Однако для построения цепи нужно знать еще вероятности переходов в
«состояние 2» и «состояние 3» при условии, что канал покинет «состояние 1».
Эти вероятности могут быть вычислены по следующим формулам:
70
