
Ч 3 Матанализ интернет-материалы
.pdf
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex |
|
|
|
|
e |
|
|
|
|
|
|||||||||
|
|
|
|
|
ex e |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
sin x |
2 |
1 |
|
|
|
|
|
|
cos x |
2 |
1 2x |
|
|
|
|
|
|
|
|||||||||||||||||
|
x 1 |
|
|
0 |
|
|
x 1 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Вычислите предел lim |
|
ln2 x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
РЕШЕНИЕ: |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
38 |
|
ln 2 x |
|
|
|
2ln x |
|
|
|
|
|
|
2 ln x |
|
|
|
2 |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
9 |
|
|
|
|
||||||||||||||||
lim |
|
|
|
lim |
|
|
|
|
|
|
lim |
|
|
|
lim |
|
|
|
|
|
|
0. |
(З |
||||||||||||||
|
|
3 |
|
3x |
2 |
|
|
|
|
|
|
3 |
|
2 |
|
|
|
x |
3 |
||||||||||||||||||
x x |
|
|
x |
|
|
|
|
|
|
|
|
x 3x |
|
|
|
x 9x |
|
|
|
|
|
|
lim |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
десь правило Лопиталя применялось дважды).
Раскройте неопределенность типа 0 |
|
|
|
|
|
|
||||||||||||||||
lim sin x 1 tg |
x |
lim |
sin x 1 |
|
lim |
cos x 1 |
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
||||||||||||||
x 1 |
2 x 1 |
ctg |
x |
x 1 |
|
|
|
|
||||||||||||||
39 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
sin |
2 |
x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
lim cos x 1 sin 2 |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вычислите предел lim (x ln x) .
x
РЕШЕНИЕ:
Имеем неопределенность типа .
|
|
|
|
|
ln x |
|
|
|
|
|
|||
|
lim (x ln x) lim |
x 1 |
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
40 |
x |
x |
|
x |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
||||||
|
|
|
ln x |
|
|
|
|
|
|
1 |
|
||
|
Исследуем lim |
lim |
|
x |
|
lim |
0 . |
||||||
|
|
|
1 |
|
|
||||||||
|
|
x |
x |
x |
|
x x |
|
||||||
Таким образом, исходный предел lim (x ln x) .
x
|
|
1 |
|
1 |
|
Вычислите предел: lim |
|
|
|
|
. |
|
|
||||
x 0 x |
e x 1 |
||||
РЕШЕНИЕ:
Предел является неопределенностью типа . Преобразуем:
41 |
|
|
1 |
|
1 |
|
1 |
|
|
|
x |
|
ex 1 x |
. |
|
|||||||
|
|
lim |
|
|
|
|
lim |
|
|
1 |
|
|
|
|
lim |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x 0 x |
e x 1 |
x 0 x |
|
|
ex 1 |
x 0 x(ex 1) |
|
|
|
|||||||||||
|
|
Дважды применяем правило Лопиталя. |
|
|
|
|
||||||||||||||||
|
lim |
ex 1 x |
lim |
|
ex |
1 |
|
|
lim |
|
e x |
|
1 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x 0 x(e x 1) |
x 0 e x 1 x e x |
|
x 0 ex ex x e x |
|
2 |
|
|||||||||||||||
1
Вычислите lim x x .
42
x
РЕШЕНИЕ:
Имеем неопределенность типа 0 .
122

1 |
y x ; |
ln y x |
1 |
|
|
|
|
|
||||
x |
x |
ln x; |
|
|
||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
ln x |
|
1 |
|
|
|||
lim ln y x lim |
|
lim |
|
x |
|
0 . |
||||||
x |
|
|
|
|||||||||
x |
|
x |
|
x 1 |
|
|
||||||
Тогда lim x |
1 |
e0 |
1. |
|
|
|
|
|
|
|||
x |
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
Вычислите предел lim tgx 2 cos x .
x 0 2
РЕШЕНИЕ:
Это неопределенность вида 0 .
Положим tgx 2 cos x y ; логарифмируем:
|
ln y 2cos x ln tgx |
2ln tgx |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя правило Лопиталя, получим: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|||||||
|
lim ln y 2 lim |
|
|
tgx |
2 lim cos x 0 . |
||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
0 |
x |
|
0 |
|
|
|
sin x |
|
x |
|
0 |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
cos2 x |
|
||||||||||||||||||
|
Таким образом, lim y e0 1. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x |
|
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
4.8. ФОРМУЛА ТЕЙЛОРА |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
Представьте функцию |
f x ax a 0,a 1 в виде |
|||||||||||||||||||||
|
могочлена третьей степени относительно х. |
||||||||||||||||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f x ax ; |
|
|
|
|
|
|
|
|
|
|
|
f 0 1; |
|
|
|
|||||||
|
f x ax ln a; |
|
|
|
|
|
|
|
f 0 ln a ; |
||||||||||||||
|
f x ax ln2 a; |
|
|
|
|
|
|
|
f 0 ln2 a ; |
||||||||||||||
44 |
f x ax ln3 a; |
|
|
|
|
|
|
|
|
f 0 ln3 a ; |
|||||||||||||
|
f 4 x ax ln4 a; |
|
|
|
|
|
|
|
|
f 4 х a x ln4 a . |
|||||||||||||
По формуле Маклорена получаем:
ax 1 x ln a ln2 a x2 ln3 a x3 R3 , 2! 3!
где R |
a x ln4 a |
x4 |
; |
0 1. |
|
||||
3 |
4! |
|
|
|
|
|
|
|
123

Выясните происхождение приближенных равенств
а) 
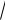 1 x 1 1 x 1 x2 , x 1; 2 8
1 x 1 1 x 1 x2 , x 1; 2 8
б) 3 1 x 1 1 x 1 x2 , x 1. 3 9
1 x 1 1 x 1 x2 , x 1. 3 9
РЕШЕНИЕ:
Равенства получаются из разложения функции (1 x) по формуле Маклорена с точностью до слагаемых второго порядка:
45 |
|
|
|
( 1) |
|
|
(1 x) 1 |
|
x |
x2 .. |
|||
1! |
2! |
|||||
|
|
|
||||
.. ( 1) ... ( n 1 ) xn n!
( 1) ... ( n)(1 x) n 1 xn 1, (n 1)!
(1 x) |
1 |
|
x |
( 1) |
x2 o x2 . |
|
|
||||
|
1! |
2! |
|
||
Многочлен 2x3 3x2 5x 1 разложите по степеням (x 1) . РЕШЕНИЕ:
f (x) 2x3 3x2 5x 1; x0 1; f ( 1) 9 .
Найдем коэффициенты многочлена Тейлора:
f |
|
(x) 6x |
2 |
6x 5 f |
|
17; |
|
|
|
( 1) |
|||||
f |
|
|
|
f |
|
18; |
|
|
(x) 12x 6 |
( 1) |
|||||
f |
|
|
|
f |
|
12; |
|
|
(x) 12 |
|
( 1) |
||||
46f IV (x) 0
f (n) (x) 0;
f (x) 9 17 (x 1) 18 (x 1)2 12 (x 1)3 . 1! 2! 3!
Учитывая, что 1! 1; 2! 1 2 ; 3! 1 2 3, получим
2x3 3x2 5x 1 9 17(x 1) 9(x 1)2 2(x 1)3 .
Запишите формулу Маклорена n–го порядка для функ-
47 |
ции f (x) 1 x . |
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
f (0) 1; x 1. |
|
f (x) 1 x ; |
124

f |
|
1 |
; |
|
|
|
f |
|
(x) (1 x) |
|
|
|
|
(0) ; |
|||
f |
|
|
2 |
; |
|
|
f |
|
(x) ( 1)(1 x) |
|
|
(0) ( -1); |
|||||
f |
|
|
|
|
3 |
; f |
|
|
(x) ( 1)( 2)(1 x) |
|
(0) ( 1)( 2); |
||||||
f (n) (x) ( 1) ... ( n 1)(1 x) n ; f (n) (0) ( 1)( 2) ... ( n 1 ),
тогда
(1 x) 1 x ( 1) x2 .. 1! 2!
.. ( 1) ... ( n 1 ) xn n!
( 1) ... ( n)(1 x) n 1 xn 1. (n 1)!
Используя формулы Маклорена для элементарных функций, напишите первые n членов формулы Маклорена для функции y ln 4 x2 .
РЕШЕНИЕ:
Преобразуем исходную функцию:
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ln 4(1 |
|
|
|
|
) ln 4 ln(1 |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
48 |
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
2 |
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
x |
2 |
|
|
|
1 |
|
|
x |
2 |
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||
|
ln 4 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..... |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
x2 |
|
n |
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
....... ( 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
4 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Окончательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ln(4 x 2 ) ln 4 |
x2 |
|
|
|
|
|
x4 |
|
|
|
|
|
|
x6 |
|
|
|
... ( 1)n 1 |
x2n |
. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 42 2 |
|
|
|
|
|
|
|
|
|
|
|
|
4n n |
||||||||||||||||||||||||||
|
Вычислите число e с точностью до 0,001. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Запишем формулу Маклорена для ex: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ex |
1 x |
x2 |
|
|
|
x3 |
|
... |
xn |
|
|
|
xn 1 |
|
e x . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
При x 1: |
|
|
|
|
|
|
|
|
|
2! |
|
3! |
|
|
|
|
|
|
|
|
|
|
|
n! |
|
(n 1)! |
|
|
|
|||||||||||||||||||||||||||||||
49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
2,718 |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||
|
|
e 1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
;0 1. |
||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
24 |
|
120 |
|
(n 1)! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|||||||||||||||||||||||||||
|
|
Наименьшее значение n , удовлетворяющее условию |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
e |
|
0,001 , равно 6, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
(n 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
125

тогда e 1 1 |
1 |
|
1 |
|
1 |
|
|
1 |
2,718. |
|
|
24 |
120 |
||||||
2 |
6 |
|
|
|
|||||
Вычислите с точностью до 10 – 3 приближенное значение
3 29 .
29 .
РЕШЕНИЕ:
Представим заданный корень так:
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
3 |
. Воспользуемся формулой Макло- |
||||
|
|
|
|
||||||
3 |
29 3 |
27 2 3 1 |
|
|
|
|
|||
|
|
|
|
||||||
27
|
рена: |
|
|
|
|
|
|
|
|
|
|
|
( 1) |
|
|
|
|
|
|
( 1)( n 1) |
|
|||||||||||||
|
(1 x) 1 |
x |
x2 ... |
xn |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1! |
|
|
|
|
|
2! |
|
|
|
|
|
|
|
n! |
||||||||||
|
|
( 1) ... ( n)(1 x) n 1 |
|
xn 1 , |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n 1)! |
|
|
|
|
|
|
|
|
|
|||||||||||
|
где последнее слагаемое представляет собой погрешность |
|||||||||||||||||||||||||||||||||
|
вычисления. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
50 |
|
Полагая |
|
|
|
|
|
|
x |
2 |
|
|
|
|
1 |
|
3,072 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
получим |
|
|
|
|
27 |
|
|
|
3 |
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
2 2 |
|
2 2 2 5 |
|
|
|
||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
3(1 |
|
|
.... Rn ) . |
||||||||||||||||||||||
|
|
29 |
||||||||||||||||||||||||||||||||
|
|
81 |
|
|
|
813 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
812 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Оценивая величины последовательных ошибок в вы- |
||||||||||||||||||||||||||||||||
|
числении 3 |
|
Rn |
|
|
, находим: |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
3 |
|
R |
|
|
|
|
3 2 2 |
0,002; |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
|
|
812 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
3 |
|
R2 |
|
|
|
3 2 2 2 5 |
0,0003. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
813 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, для вычисления с заданной точностью достаточно взять три члена, которые предшествуют остатку R2, т.е.
3  29 3(1 0,024 0,0006) 3,072 .
29 3(1 0,024 0,0006) 3,072 .
Используя разложение по формуле Маклорена, вычислите |
||||||||
предел lim |
1 cos3 |
x |
. |
|
|
|
||
5x2 +7x3 |
|
|
|
|||||
|
x 0 |
|
|
|
|
|||
РЕШЕНИЕ: |
|
|
|
|
|
|
||
51 1 cos3 x 1 cos x 1 cos x cos2 x ; |
0,3 |
|||||||
C точностью до бесконечно малых о x2 |
получаем: |
|||||||
3 |
x |
|
3 1 cos x |
|
|
|
||
|
1 cos |
|
|
|
||||
lim |
lim |
|
. |
|
||||
|
|
|
5x2 |
|
|
|||
x 0 5x2 +7x3 |
x 0 |
|
|
|
|
|||
Заменим cos x его разложением по формуле Маклорена: |
||||||||
126

|
cos x 1 |
x2 |
о x2 , тогда |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
2! |
|
|
|
|
3 1 cos x |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 cos |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
lim |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
5x2 |
|
|
|
|
|
|
|
|||||||||||||||
|
x 0 5x2 +7x3 |
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
3 |
|
|
|
x2 |
o x2 |
|
|
3 |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
lim |
2 |
|
|
lim |
|
|
2 |
, |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
5 x 0 |
|
|
|
|
|
|
5 x 0 x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Поскольку |
x2 |
|
o x2 |
~ |
|
x2 |
при x 0 . |
|
||||||||||||||||||||||
|
2 |
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Окончательно |
|
lim |
1 cos3 x |
|
|
|
3 |
. |
|
|||||||||||||||||||||
|
|
|
|
|
+7x3 |
10 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 5x2 |
|
|
|
|||||||||||||
4.9.ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ
4.9.1.Возрастание и убывание функций
№ |
|
|
|
|
Задание |
По данному графику функции y y x |
|||||
постройте вид графиков y , y . |
|||||
РЕШЕНИЕ: |
|
|
|
y x убывает, |
|
1) На интервале 3;0 |
|
||||
y 0 , |
lim |
|
|
0 0 . |
|
y , |
y |
|
|||
|
x 3 0 |
|
|
|
|
2) На интервале 0;2 |
|
y x возрас- |
|||
тает, y 0 , |
|
|
|
|
|
|
|
|
|
|
|
lim y . |
|
|
|
|
|
x 2 0 |
|
|
|
y x убывает, |
|
3) На интервале 2;5 |
|
||||
1 y 0 , |
lim |
|
|
|
|
y . |
|
|
|
||
|
x 5 0 |
|
|
|
|
4)y 7 0 .
5)На интервале 5;7 y x возраста-
ет, y |
0 , на интервале 7;9 |
y x |
убывает, y 0.
Эти соображения позволяют построить примерный график y x .
6) y 3, 5 |
y 7 0 |
Та же последовательность действий, примененная к графику функции
y x , дает примерный график второй
127

|
производной y x . |
|
|
|
|
По данному графику |
|
|
|
|
производной y постройте вид |
|
||
|
графика функции y y x . |
|
||
|
РЕШЕНИЕ: |
|
|
|
|
1) На интервале 3;1 |
y 0 , |
|
|
|
y x возрастает, lim |
y , т.е., скорость возрастания |
y x |
|
|
x 1 0 |
|
||
|
также неограниченно возрастает, а следовательно, и сама функция |
|||
|
y x неограниченно возрастает, таким образом, x 1 – вертикальная |
|||
|
асимптота графика. |
|
|
|
|
2) На интервале 1;3 y 0 , y x возрастает, причем |
|
||
|
lim y , (чем ближе точка к x 1 – справа от нее, тем больше |
|||
2 |
x 1 0 |
|
x 1 – |
|
скорость возрастания), что указывает, что lim y , т.е., |
||||
|
||||
|
|
x 1 0 |
|
|
|
точка разрыва второго рода. |
|
||
|
3) В точке x 3 производная |
|
||
|
меняет знак с «+» на «–», x 3 – |
|
||
|
точка локального максимума. |
|
||
|
4) На интервале 3;7 y 0 , |
|
||
|
y x убывает. |
|
|
|
5)В точке x 7 производная меняет знак с «–» на «+», x 7 – точка локального минимума.
6)При x 7 функция возрастает.
Эти |
соображения |
позволяют |
|
|
|
|
|
|
||||
построить примерный график |
y x : |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
Функция |
f x e x возрастает |
в своей |
области определения, |
так |
как |
|||||||
3 |
f x e |
x |
|
|
|
|
|
|
|
|
|
|
|
0 при любых |
x R . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
f x |
|
|
|
|
|
|
|
|||||
Функция |
f x x sin x возрастает на |
|
интервале |
0, 2 , |
так |
как |
для |
|||||
x 0, 2 |
f x 1 cos x 0 . |
|
|
|
|
|
|
|
||||
4 |
|
|
|
|
|
f 0 0 , то |
f x 0 , |
значит |
x sin x |
для |
||
Полезный вывод: поскольку |
||||||||||||
x 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
128



