3.3.1. Модели потоков событий

3.3.1.1. Простейший поток отказов

Существует множество математических моделей потоков событий. Наиболее часто при решении задач надежности восстанавливаемой аппаратуры используют простейший поток отказов [3.1, 3.2, 3.3, 3.4].

Простейший поток отказов удовлетворяет одновременно трем условиям: стационарности, ординарности, отсутствию последействия.

Стационарность случайного потока событий (времени возникновения отказов) означает, что на любом промежутке времени Δt_i вероятность возникновения n отказов зависит только от значения n и величины промежутка Δt_i, и не зависит от сдвига по оси времени. Следовательно, при Δt_i= Δt_i+1= Δt_i+m  вероятность появления n отказов по всем интервалам одинакова.

P_n(Δt_i)= P_n(Δt_i+1)= … P_n(Δt_i+m). (3.38)

Условие стационарности означает, что параметр потока отказов ω(t) = λ = const

Ординарность потока означает невозможность появления в один и тот же момент времени более одного отказа, то есть

lim P_n(Δt)=0 (для n>1) . (3.39) 

^Δt→0

Отсутствие последействия означает, что вероятность наступления n отказов в течение промежутка Δt_i не зависит от того, сколько было отказов и как они распределялись до этого промежутка времени. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.

Если отказы элементов происходят мгновенно, отказ любого элемента приводит к отказу всей системы, старение элементов отсутствует (λ= const), то поток отказов в системе можно считать простейшим.

Свойства простейшего потока

1. Случайные события, образующие простейший поток, распределены по закону Пуассона [3.1, 3.2]:

при n 0,(3.40)

где P_n(t) - вероятность возникновения в течение времени t ровно n отказов, λ – параметр распределения, совпадающий с параметром потока событий.

2. Если в выражении (3.3) принять n = 0, то получим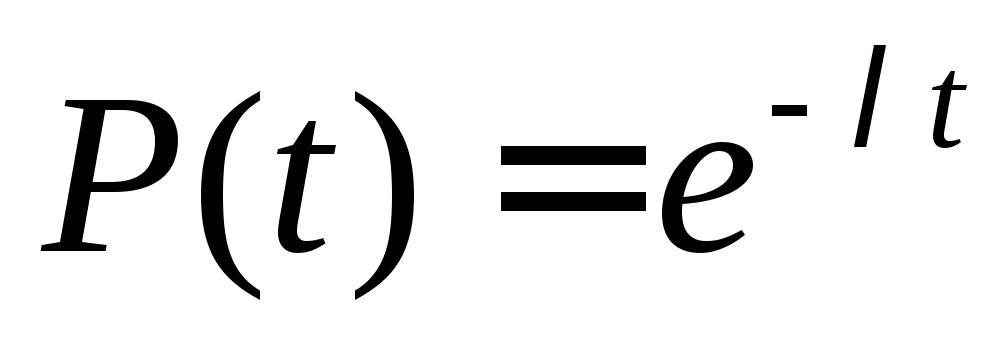- вероятность безотказной работы объекта за время t при интенсивности отказов λ = const.

Таким образом, при пуассоновском потоке отказов промежуток времени между отказами подчиняется экспоненциальному распределению.

3. Среднее число отказов на отрезке времени [0,t] - W(t) = λt.

3.3.1.2. Потоки Эрланга

Нарушение условий стационарности или наличие последействия приводит к непростейшим потокам событий (отказов). Например, к таким потокам относятся потоки Эрланга к- го порядка, которые возникают при «просеивании» простейшего потока. Поток Эрланга к- го порядка- поток, получающийся в результате сохранения каждого к-го события (отказа) в простейшем потоке. При к=1 поток Эрланга – простейший.

Дифференциальный закон распределения появления события в потоке Эрланга имеет вид:

, (3.41)

где λ – интенсивность простейшего потока отказов.

Выражение (3.4) отвечает гамма- расределению ( см. п. 3.3.3).

Интенсивность потока Эрланга

. (3.42)

Математическое ожидание времени между появлениями событий:

(3.43)

Дисперсия времени между событиями:

. (3.44)

Можно использовать модели потоки Эрланга к-го порядка при рассмотрении потоков отказов в резервированной системе ( см. раздел 4) с кратностью резервированияk-1.