Информация о вкладах в банке для расчета средних значений

В октябре известен средний размер вкладов каждого вида х и количество вкладов f Следовательно, для расчета среднего размера вклада по двум видам применяем формулу средней арифметической взвешенной, руб.:

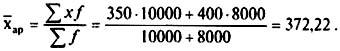
В ноябреизвестен средний размер вкладов каждого вида, а количество вкладов - не известно, но зато имеются данные об общих суммах этих вкладов.

Путем деления сумм вкладов w каждого вида на их средний размер вклада x можно определить веса - число вкладов / по их видам, а затем определить средний размер вклада по двум видам по формуле средней арифметической взвешенной. Однако, если в расчете использовать среднюю гармоническую взвешенную, то отпадает необходимость предварительных расчетов весов - размеров вкладов по каждому виду, поскольку эта операция заложена в саму формулу.

Итак, средний размер вклада в ноябрепо двум их видам находим по формулесредней гармонической взвешенной, руб.:

66

5.2.5. Средняя квадратическая и средняя кубическая

В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая(например, для вычисления средней величины стороны п квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны п кубов).

Формулы для расчета средней квадратической: #P#

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

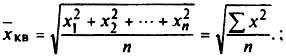(5.12)

средняя квадратическая взвешенная

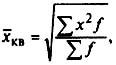(5.13)

где f- веса.

Формулы для расчета средней кубической аналогичны:

средняя кубическая простая

67

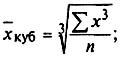(5.14)

средняя кубическая взвешенная

(5.15)

Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов х, и из их отклонений от средней ( х -x ¯ ) при расчете показателей вариации (см. 5.3).

Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней может быть средняя прогрессивнаякак одна из частных средних, вычисляемая не для всех, а только для "лучших" (например, для показателей выше или ниже средних индивидуальных).

68

5.3. Показатели вариации

Вариация- это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д.

Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.

Исследование вариации в статистике имеет большое значение, помогает познать сущность изучаемого явления. Особенно актуально оно в период формирования многоукладной экономики. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию (например, о продолжительности жизни людей, доходах и расходах населения, финансовом положении предприятия и т.п.) для принятия научно обоснованных управленческих решений.

Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом - эти отличия велики, т.е. в одном случае вариация признака мала, а в другом - велика, это имеет весьма важное значение для характеристики надежностисредней величины.

71

Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот, - чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другиепоказатели, характеризующие отклонения отдельных значений от общей средней.

Это можно показать на таком примере. Предположим, что одинаковую работу выполняют две бригады, каждая - из трех человек. Пусть количество деталей, шт., изготовленных за смену отдельными рабочими, составляло:

в первой бригаде - 95, 100, 105 (x¯₁= 100 шт.);

во второй бригаде - 75, 100, 125 (x¯₂= 100 шт.).

Средняя выработка на одного рабочего в обеих бригадах одинакова и составляет x¯₁= x¯₂= 100 шт., однако колеблемость выработки отдельных рабочих в первой бригаде значительно меньше, чем во второй.

Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.

К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.

Самым элементарным показателем вариации признака является размах вариации R,представляющий собой разность между максимальным и минимальным значениями признака:

В нашем примере размах вариации сменной выработки деталей составляет: в первой бригаде - R₁= 10 шт. (т.е. 105 - 95); во второй бригаде - R₂= 50 шт. (т.е. 125 - 75), что в 5 раз больше.

Это свидетельствует о том, что при численном равенстве средняя выработка первой бригады более "устойчива". Размах вариации может служить базой расчета возможных резервов роста выработки. Таких резервов больше у второй бригады, поскольку в случае достижения всеми рабочими максимальной для

72

этой бригады выработки деталей, ею может быть изготовлено 375 шт., т.е. (3x125), а в первой - только 315 шт., т.е. (3 х 105).

Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением ее размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и даёт обобщённую характеристику. Простейший показатель такого типа - среднее линейное отклонение.

Среднее линейное отклонениеd¯ представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: (x - x¯),

Среднее линейное отклонение:

для несгруппированных данных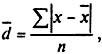(5.18)

где n - число членов ряда;

для сгруппированных данных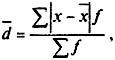(5.19)

где Σf- сумма частот вариационного ряда.

В формулах (5.18) и (5.19) разности в числителе взяты по модулю, (иначе в числителе всегда будет ноль - алгебраическая сумма отклонений вариантов от их средней арифметической). Поэтому среднее линейное отклонение как меру вариации признака применяют в статистической практике редко (только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл). С его помощью, например, анализируется состав работающих, ритмичность производства, оборот внешней торговли.

Дисперсияпризнака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

простая дисперсия для несгруппированных данных

(5.20)

73

взвешенная дисперсия для вариационного ряда

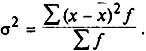(5.21)

Формула (5.21) применяется при наличии у вариантов своих весов (или частот вариационного ряда).

Формулу для расчета дисперсии (5.20) можно преобразовать, учитывая, что

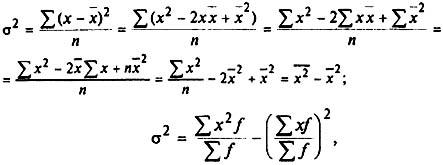(5.22)

т.е. дисперсия равна разности средней из квадратов вариантов и квадрата их средней.

Техника вычисления дисперсии по формулам (5.20), (5.21) достаточно сложна, а при больших значениях вариантов и частот может быть громоздкой.

Расчет можно упростить, используя свойства дисперсии (доказываемые в математической статистике). Приведем два из них:

первое-если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится;

второе-если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i² раз.

Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

74

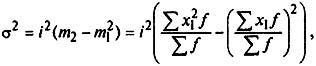(5.23)

где - дисперсия, исчисленная по способу моментов;

i - величина интервала;

новые (преобразованные) значения вариантов

(А - условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);

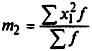- момент второго порядка;

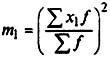- квадрат момента первого порядка.

Расчет дисперсии по формуле (5.23) менее трудоемок.

Дисперсия имеет большое значение в экономическом анализе. В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия. Ниже, в частности, будет показано разложение дисперсии на соответствующие элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений.

Среднее квадратическое отклонениеа равно корню квадратному из дисперсии:

для несгруппированных данных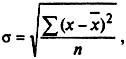(5.24)

для вариационного ряда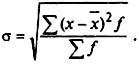(5.25)

Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.

Обозначим: 1 - наличие интересующего нас признака; 0 - его отсутствие; р - доля единиц, обладающих данным признаком; q -

75

доля единиц, не обладающих данным признаком; р + q =1. Исчислим среднее значение альтернативного признака и его дисперсию.Среднее значение альтернативного признака

(5.26)

так как р + q = 1.

Дисперсия альтернативного признака

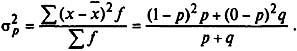(5.27)

Подставив в формулу дисперсии q = 1 - р , получим

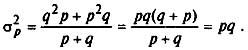(5.28)

Таким образом, - дисперсия альтернативного при знака равна произведению доли единиц, обладающих призна ком, на долю единиц, не обладающих данным признаком.

Например, если на 10 000 человек населения района прихо дится 4500 мужчин и 5500 женщин, то

Дисперсия альтернативного признака

Предельное значение дисперсии альтернативного признака равно 0,25. Оно получается при р - 0,5 .

Среднее квадратическое отклонение альтернативного признака

(5.29)

Если, например, 2% всех деталей бракованные (р = 0,02), то 98% - годные (q = 0,98), тогда дисперсия доли брака

= 0,02-0,98 = 0,0196.

Среднее квадратическое отклонение доли брака составит:

При вычислении средних величин и дисперсии для интервальных рядов распределения истинные значения признака заменяются

76

центральными (серединными) значениями интервалов, которые отличаются от средней арифметической значений, включенных в интервал, Это приводит к появлению систематической погрешности при расчете дисперсии, В.Ф.Шеппард установил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала (т.е. i²/12) как в сторону занижения, так и в сторону завышения величины дисперсии.

Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по большому количеству исходных данных (n>500). Однако исходя из того, что в ряде случаев обе погрешности, действуя в противоположных направлениях, нейтрализуются и компенсируют друг друга, можно иногда отказаться от введения поправок.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина.

В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.

Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации - коэффициент вариации.

Коэффициент вариациипредставляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

(5.30)

77

Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считаетсяколичественно однородной,если коэффициент вариации не превышает 33 %.

Покажем расчет различными способами показателей вариации на примере данных о сменной выработке рабочих бригады, представленных интервальным рядом распределения (табл. 5.7).

Исчислим среднесменную выработку, шт.:

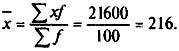
Рассчитаем дисперсию выработки по (5.21):

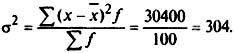
Найдем среднее квадратическое отклонение, шт.:

Определим коэффициент вариации, %:

Таким образом, данная бригада рабочих достаточно однородна по выработке, поскольку вариация признака составляет лишь 8%.

Теперь выполним расчет дисперсии по формуле (5.22) и по способу моментов по формуле (5.23), для расчета воспользуемся данными табл. 5.7, графы 8-11.

Расчет дисперсии по формуле (5.20):

Расчет дисперсии по способу моментов, см. формулу (5.21):

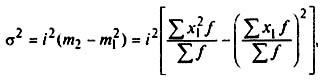
где А - 50 - центральный вариант с наибольшей частотой; i = 20 - величина интервала данного ряда;

78

Таблица 5.7