TETs_Sobolev
.pdf





476 |
Г л а в а 10 |
10.2. Линии без потерь в различных режимах работы
10.2.1. Цели изучения
1.Исследование распределения амплитуд напряжения и тока в длинной линии без потерь в режимах КЗ и ХХ, а также в режиме согласованной нагрузки.
2.Исследование распределения амплитуд напряжения и тока в длинной линии без потерь в режиме несогласованной нагрузки при
0< Zн < 1.
3.Ознакомление с понятиями коэффициент бегущей волны и
коэффициент стоячей волны.
4. Исследование входного сопротивления длинной линии без потерь.
10.2.2. Основные теоретические положения
10.2.2.1. Выразим напряжение и ток в любом сечении линии через коэффициент отражения. Для этого вынесем за скобку в выражениях (10.9) и (10.10) постоянную A1:
|
|
y |
|
A2 |
|
y |
|
A1 |
|
|
|
|
|
|
y |
A2 |
|
y |
|||||||||||
U(y) = A1 (e |
|
|
+ |
|
|
|
e |
|
); I(y) = |
|
|
|
(e |
|
|
|
e |
|
): |
||||||||||
|
|
A1 |
|
Zв |
|
|
A1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
С учётом (10.13) и (10.14) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
U(y) = |
U2 + I2Zв |
(e |
|
|
y + n2e |
|
|
|
|
y); |
|
|
(10:18) |
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I(y) = |
U2 + I2Zв |
(e |
|
y |
n2e |
|
|
|
y): |
|
|
(10:19) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2Zв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10.2.2.2. Рассмотрим согласованную на входе (Zв = Rи) линию без потерь ( = 0, = j , Zв = Zв) в режиме короткого замыкания. В этом режиме Zн = 0, следовательно,
|
|
Z |
н |
Zв |
0 |
Zв |
|
||
n2 |
= |
|
|
|
= |
|
|
= 1 |
|
Zн |
+ Zв |
0 + Zв |
|||||||
|
|
|
|
||||||
иU2 = 0. Подставим эти значения и упомянутые выражения для
иZв в выражение (10.18):
|
0 + I |
2Zв |
|
j y |
|
j y |
|
ej y e |
j y |
|
U(y) = |
|
|
(e |
|
1e |
|
) = I2Zв |
|
|
= |
|
|
|
|
2 |
|
|||||
2 |
|
= jI2Zв sin( y): |
(10:20) |
|||||||
|
|
|
|
|||||||
Это выражение для комплексной амплитуды напряжения. Аналогично можно получить следующее выражение для комплексной амплитуды тока:
I(y) = I2 cos( y): |
(10:21) |

Цепи с распределёнными параметрами |
477 |
Для того чтобы перейти от комплексных амплитуд U(y) и I(y) к функциям времени (т. е. к мгновенным значениям), умножим комплексные амплитуды на оператор поворота ej!t и выделим из полученных выражений вещественные части. В результате получим:
u(t; y) = jI2Zв sin( y)j cos(!t + =2 + ); |
(10:22) |
i(t; y) = jI2cos( y)j cos(!t + ): |
|
Слагаемое =2 в фазе напряжения (10.22) появилось за счёт множителя j = ej =2 в выражении (10.20). Как видим, в любом сечении линии сдвиг фазы между напряжением и током равен 90◦. Активная мощность в этом режиме не передаётся, так как P = UI cos 90◦ = = UI 0 = 0. Распределения значений амплитуд напряжения и тока вдоль линии описываются выражениями:
Um(y) = jI2Zв sin( y)j; |
Im(y) = jI2 cos( y)j: |
(10:23) |
||
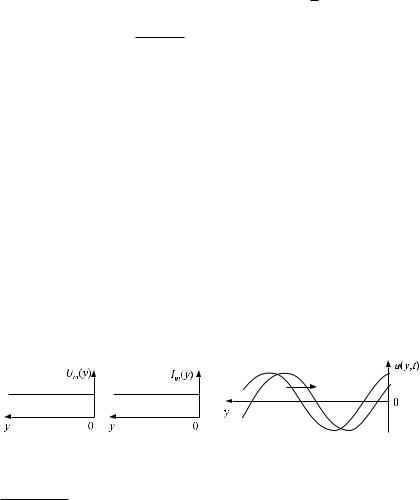
Соответствующие графики изображены на рис. 10.14. |
|
|
||
По рассматриваемой линии |
|
|
|
|
распространяются две волны (па- |
|
|
|
|
дающая и отражённая), так как |
|
|
|
|
n2 = 1 и n1 = 0 (линия не сог- |
|
|
|
|
|
|
|
|
|
ласована на выходе и согласова- |
|
|
|
|
на на входе). Там где эти вол- |
|
|
|
|
|
|
|
|
|
ны встречаются в противофазе, |
|
|
|
|
образуются узлы, а там где вол- |
|
|
|
|
ны встречаются в фазе, образу- |
|
|
|
|
ются пучности. Так как в выра- |
|
Рис. 10.14. Распределение амплитуд |
||
жения для амплитуд (10.23) вре- |
|
гармонического напряжения и тока |
||
мя не входит, то положения узлов |
|
вдоль линии без потерь в режиме КЗ |
||
и пучностей с течением времени не изменяется. Отсюда и название этого режима — режим стоячих волн.
На любом участке длиной =4 происходит обмен энергией между электрическим и магнитным полями (потерь энергии нет).
Так как имеем линию без потерь, то ослабление сигнала отсутствует. Амплитуда отражённой волны равна амплитуде падающей волны, но имеет место противоположность в знаках (так как n2 = 1). Поэтому в конце линии (и в сечениях y = k =2, где k = 1; 2; 3:::) напряжения падающей и отражённой волн полностью компенсируют друг друга, а в пучностях эти напряжения складываются. В тех сечениях, где образуются пучности напряжения, имеют место узлы тока, а там, где образуются узлы напряжения, имеют место пучности тока.
10.2.2.3. Рассмотрим согласованную на входе (Zв = Rи) линию без потерь ( = 0, = j , Zв = Zв) в режиме холостого хода. В этом

478 |
|
|
|
Г л а в а 10 |
режиме Zн = 1, следовательно, |
|
|
||
n2 = |
Zн Zв |
= |
Zн |
= 1 |
|
|
|||
|
Zн + Zв |
Zн |
||
иI2 = 0. Подставим эти значения и упомянутые выражения для
иZв в выражение (10.18):
U(y) = |
U2 + 0 |
(ej y + 1e |
j y) = U2 |
ej y + e j y |
= U2 cos( y): (10:24) |
2 |
|
||||
|
|
2 |
|
||
Это выражение для комплексной амплитуды напряжения. Аналогично можно получить следующее выражение для комплексной амплитуды тока:
I(y) = j U2 sin( y): Zв
Для перехода от комплексных амплитуд U(y) и I(y) к функциям времени (т. е. к мгновенным значениям) умножаем их на оператор поворота еj!t и выделяем из полученных выражений вещественные
части. В результате получаем: |
|
|
|
|
|
|||
u(t; y) = jU2 cos( y)j cos(!t + |
); |
|
|
|||||
|
U2 |
|
|
|
|
|
|
|
i(t; y) = Zв |
sin( y) cos (!t + |
2 |
|
+ |
): |
|||
|
|
|
|
|
|
|
|
|
Как видим, в любом |
сечении линии |
сдвиг фазы между током и |
||||||
напряжением равен 90◦. Активная мощность в этом режиме так же не передаётся, так как P = UI cos 90◦ = UI 0 = 0. Распределения значений амплитуд напряжения и тока вдоль линии описываются выражениями:
|
|
|
U2 |
|
|
|
Um(y) = jU2 cos( y)j; |
Im(y) = |
|
Zв |
sin( y) |
: |
|
|
|
|
|
|
|
|
Соответствующие графики изображены на рис. |
10.15. |
|
||||
|
Как видим, в рассматривае- |
|
мом случае также имеет место |
|
режим стоячих волн. В конце ли- |
|
нии отражённая волна напряже- |
|
|
|
ния имеет те же значения амп- |
|
литуды и фазы, что и падающая |
|
|
|
волна напряжения, так как коэф- |
|
фициент отражения n2 = 1. По- |
|
этому амплитуды этих волн скла- |
Рис. 10.15. Распределение амплитуд |
дываются и образуют пучность |
гармонического напряжения и тока |
напряжения. Из амплитуды па- |
вдоль линии без потерь в режиме ХХ |
дающей волны тока в конце ли- |