TETs_Sobolev
.pdf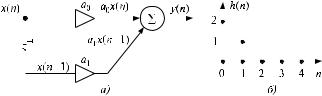

Частотная фильтрация электрических сигналов |
381 |
исключено. Каждая из сумм является z-образом входной последовательности, поэтому имеем:
Y (z) = a0X(z) + a1z 1X(z);
или
Y (z) = X(z)(a0 + a1z 1): |
(8:30) |
Теперь можно сформулировать простое правило z-преобразования линейного разностного уравнения:
Если члены с сомножителями x(n k) и y(n k) фигурируют в разных частях уравнения, то нужно z-образ каждой последовательности умножить на записанное в соответствующей части выражение, в котором упомянутые сомножители заменены сомножителями z k.
Это правило справедливо для линейных разностных уравнений, описывающих законы функционирования фильтров любого порядка.
Системной (передаточной) функцией цифрового фильтра называется отношение z-образа выходной последовательности к z-образу входной последовательности:
H(z) = |
Y (z) |
: |
(8:31) |
|
X(z) |
||||
|
|
|
||
|
|
|
|
Системную функцию рассматриваемого фильтра можно получить из (8.30):
H(z) = Y (z) = a0 + a1z 1: X(z)
Структурная схема трансверсального фильтра второго порядка представлена на рис. 8.104. Линейное разностное уравнение, описывающее закон функционирования этого фильтра, имеет вид
y(n) = a0x(n) + a1x(n 1) + a2x(n 2):
Системная функция имеет вид
H(z) = a0 + a1z 1 + a2z 2:
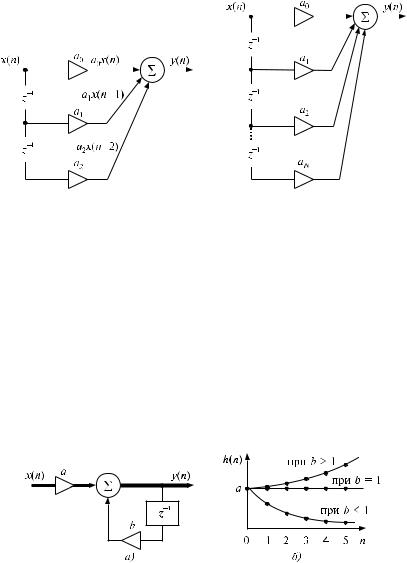
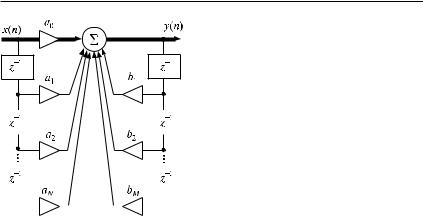
В общем случае имеем трансверсальный фильтр N-го порядка, структурная схема которого представлена на рис. 8.105.
Линейное разностное уравнение, описывающее закон функционирования этого фильтра, имеет вид
∑N
y(n) = akx(n k):
k=0
382 |
|
|
|
|
|
|
|
|
|
|
|
Г л а в а 8 |
|||||
|
|
Системная функция имеет вид |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H(z) = |
akz k: |
(8:32) |
|||||||
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.104. Трансверсальный фильтр |
Рис. 8.105. Трансверсальный фильтр |
второго порядка |
N-го порядка |
8.5.2.6. Рассмотрим рекурсивный фильтр первого порядка, схема которого изображена на рис. 8.106,a. Его выходной сигнал формируется в виде суммы двух сигналов: входного сигнала, умноженного на константу a, и задержанного на один такт выходного сигнала, умноженного на константу b. Поэтому линейное разностное уравнение, описывающее закон функционирования этого фильтра, имеет вид
y(n) = ax(n) + by(n 1): |
(8:33) |
Подадим на вход единичный импульс (8.28) и рассчитаем по формуле (8.33) выходную последовательность чисел, т. е. импульсную характеристику h(n). Процесс и результат расчёта представлены в табл. 8.20. Как видим, импульсная характеристика рассматриваемой цепи бесконечна во времени. Её графики (для разных случаев при
Рис. 8.106. Рекурсивный фильтр первого порядка (a) и его импульсные характеристики при положительных значениях параметров a и b (b)
Частотная фильтрация электрических сигналов |
383 |
a > 0 и b > 0) приведены на |
Таблица 8.20 |
рис. 8.106,b. При jbj |
> 1 цепь |
n |
x(n) (n) x(n 1) |
|
|
|
y(n) h(n) |
|
||||||
неустойчива. При b =1 цепь |
0 |
1 |
0 |
|
|
a 1 + b 0 = a |
|
|||||||
является генератором одина- |
|
|
|
|||||||||||
ковых чисел. При 0<b<1 это |
1 |
0 |
a |
|
a |
a 0 + b a = ab |
2 |
|||||||
2 |
0 |
ab |
|
|
0 + b |
ab = ab |
|
|||||||
БИХ-фильтр, |
аналогичный |
3 |
0 |
ab |
2 |
|
0 |
|
2 |
= ab |
3 |
|||
|
a 0 + b ab |
|
||||||||||||
по своим свойствам RC-цепи. |
: : : |
: : : |
: : : |
|
|
|
: : : |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдём системную функцию рассматриваемого фильтра. |
Для |
|||||||||||||
этого сначала преобразуем линейное разностное уравнение (8.33), соб- |
||||||||||||||
рав члены с сомножителями x(n |
k) и y(n k) в его разных частях: |
|||||||||||||
|
|
y(n) by(n 1) = ax(n): |
|
|
|
|
|
|
|
|
|
|||
Далее применим к обеим частям полученного равенства z-преоб- |
||||||||||||||
разование, воспользовавшись выведенным ранее правилом: |
|
|
|
|||||||||||
|
|
Y (z)(1 bz |
1) = X(z)a; |
|
|
|
|
|
|
|
|
|
||
откуда на основании (8.31) получим |
|
|
|
|
|
|
|
|
|
|
||||
выражение для системной функции: |
|
|
|
|
|
|
|
|
|
|
||||
Y (z) |
= 1 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
H = X(z) |
bz 1 : |
(8:34) |
|
|
|
|
|
|
|
|
|
|
||
Структурная схема рекурсивно- |
|
|
|
|
|
|
|
|
|
|
||||
го фильтра второго порядка предс- |
|
|
|
|
|
|
|
|
|
|
||||
тавлена на рис. 8.107. Линейное раз- |
|
|
|
|
|
|
|
|
|
|
||||
ностное уравнение, описывающее за- |
|
|
|
|
|
|
|
|
|
|
||||
кон функционирования этого филь- |
|
|
|
|
|
|
|
|
|
|
||||
тра, имеет вид |
|
|
|
Рис. 8.107. Рекурсивный фильтр |
|
|||||||||
y(n) = a0x(n) + a1x(n 1) + |
|
второго порядка |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
+ b1y(n 1) + b2y(n 2): |
|
|
|
|
|
|
|
|
|
|
|
|||
Приведённое уравнение имеет вид |
|
|
|
|
|
|
|
|
|
|
||||
y(n) b1y(n 1) b2y(n 2) = a0x(n) + a1x(n 1): |
|
|
|
|||||||||||
После выполнения z-преобразования имеем |
|
|
|
|
|
|
|
|
|
|||||
Y (z)(1 |
b1z 1 |
b2z 2) = X(z)(a0 + a1z |
1); |
|
|
|
|
|||||||
откуда получаем выражение для системной функции |
|
|
|
|
|
|
|
|||||||
|
|
Y (z) |
= |
a0 + a1z |
1 |
: |
|
|
|
|
|
|
|
|
|
H = |
b1z 1 |
b2z 2 |
|
|
|
|
|
|
|
||||
|
|
X(z) 1 |
|
|
|
|
|
|
|
|
|
|||
Можно показать, что при a0 = 1 рассматриваемый фильтр ана- |
||||||||||||||
логичен по своим свойствам колебательному контуру. |
|
|
|
|
|
|
||||||||
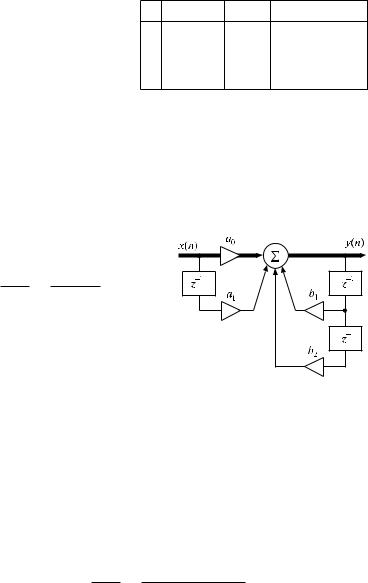
В общем случае имеем рекурсивный фильтр M-го порядка, струк- |
||||||||||||||
турная схема которого представлена на рис. 8.108. Обычно M > N. |
||||||||||||||
384 Г л а в а 8
Линейное разностное уравнение, описывающее закон функционирования этого фильтра, имеет вид
|
|
|
|
|
|
|
N |
|
M |
|
||
|
|
|
|
|
|
|
∑ |
|
∑ |
|
||
|
|
|
|
|
|
|
y(n) = akx(n k) + |
|
|
bky(n k): |
||
|
|
|
|
|
|
|
k=0 |
|
k=1 |
|
||
|
|
|
|
|
|
|
Системная функция имеет вид |
|||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
akz |
k |
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
H(z) = |
|
∑ |
|
: |
(8:35) |
|
|
|
|
|
|
|
|
M |
|
|||
|
|
|
|
|
|
1 |
∑ |
|
|
|
||
|
|
|
|
|
|
bkz k |
|
|||||
k=1
Полагая некоторые из коэффициентов ak и bk равными нулю, можно
получить любой из ранее описанных фильтров.
8.5.2.7. Заменяя в выражениях системных функций (8.32) и (8.35) переменную z выражением ej!T , получаем выражения комплексных передаточных функций:
для трансверсального фильтра
|
|
|
|
N |
|
|
H(j!) = H(z)jz=ej! = |
∑ |
|
|
|||
ake j!kT ; |
||||||
для рекурсивного фильтра |
|
|
k=0 |
|
|
|
|
|
N |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ake |
j!kT |
|
( ) = |
( )jz=e |
= |
|
k=0 |
|
|
|
M |
: |
||||
H j! |
H z |
j!T |
∑ |
|||
|
|
|
|
∑ |
|
|
|
|
1 |
bke j!kT |
|||
k=1
Выражения для передаточных АЧХ и ФЧХ несложно получить из выражения H(j!) как модуль jH(j!)j и аргумент arg(H(j!)) соответственно.
Выведем в качестве примера выражение для передаточной АЧХ рекурсивного фильтра первого порядка (см. рис. 8.106,a), системная функция которого описывается выражением (8.34). Заменив в (8.34) переменную z выражением ej!T , получаем следующее выражение для
комплексной передаточной функции: |
|
|
|
||||
H(j!) = |
a |
= |
a |
|
|
= |
|
|
|
|
|
||||
1 be j!T |
1 [b cos( !T ) + jb sin( |
!T )] |
|||||
|
= |
|
|
a |
: |
(8:36) |
|
|
|
|
|||||
|
1 |
b cos !T + jb sin !T |
|||||
Частотная фильтрация электрических сигналов |
385 |
||||||
Выражение для передаточной АЧХ определяем как модуль полу- |
|||||||
ченного выражения: |
|
|
|
||||
H(!) = jH(j!)j = |
|
|
a |
= |
|||
|
|
|
|
||||
√ |
|
|
|
||||
(1 |
ab cos !T )2 + (b sin !T )2 |
||||||
= |
|
|
|
= |
|
||
√ |
|
|
|
||||
12b cos !T + b2 cos2 !T + b2 sin2 !T
= |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
p |
|
|
|
|
|
|
|
a |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|||||||||
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
2b cos !T + b2(cos2!T + sin2 !T ) |
1 |
|
|
2b cos !T + b2 |
|||||||||||||||||||||||||||||||||||
Найдём экстремальные значения модуля комплексного коэффи- |
||||||||||||||||||||||||||||||||||||||||
циента передачи для случая a > 0 и 0 < b < 1. |
|
При !T = 0 (т. е. |
||||||||||||||||||||||||||||||||||||||
при ! = 0) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
H = |
p |
|
a |
= |
|
|
|
|
|
|
|
|
a |
= |
|
|
|
|
a |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 b |
||||||||||||||||||||||
|
|
|
1 2b + b2 |
|
|
√ |
(1 b)2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
!д |
|
|
|
|
|
|
|
||||||||||||||||
При |
!T = (т. е. при ! = |
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
, где !д — частота |
||||||||||||||||||||||
|
T |
|
T |
2 |
|
2 |
|
|||||||||||||||||||||||||||||||||
дискретизации) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
H = |
p |
|
a |
= |
|
|
|
|
|
|
|
|
a |
= |
|
|
|
|
a |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|||||||||||||||||
|
|
|
|
√ |
|
|
|
|
|
|
1 + b |
|||||||||||||||||||||||||||||
|
|
|
1 + 2b + b2 |
|
|
(1 + b)2 |
||||||||||||||||||||||||||||||||||
При !T = 2 (т. е. при ! = 2 =T = !д) имеем |
||||||||||||||||||||||||||||||||||||||||
|
|
|
H = |
p |
a |
|
= |
|
|
|
|
|
|
|
a |
= |
|
|
|
a |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
√ |
|
|
|
|
|
1 b |
||||||||||||||||||||||||||||||||
и т. д. |
1 2b + b2 |
|
(1 b)2 |
|||||||||||||||||||||||||||||||||||||
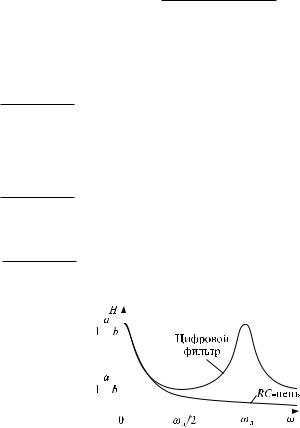
На рис. 8.109 приведена АЧХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
рассматриваемого цифрового фи- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
льтра, рассчитанная при a = 1 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
b = 0;6 (сплошная линия) и АЧХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
аналоговой RC-цепи (пунктирная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
линия). |
Как видим, при часто- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
тах от 0 до !д=4 упомянутые АЧХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
примерно совпадают, а выше |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
!д=2 принципиально различают- |
Рис. 8.109. АЧХ цифрового фильтра и |
|||||||||||||||||||||||||||||||||||||||
ся. Амплитудно-частотные харак- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RC-цепи |
|||||||||||||||||||||
теристики этого, да и любого цифрового фильтра, имеют периодический характер, что объясняется наличием в их выражениях тригонометрических функций. Следовательно, пользоваться цифровыми фильтрами можно только для сигналов со спектрами, ограниченными частотой !д=2 (за исключением гребенчатых фильтров, в которых преднамеренно используется упомянутый эффект периодичности).
386 |
Г л а в а 8 |
8.5.3. Задание для предварительного расчёта
8.5.3.1. Найти z-образ последовательности 1, 0.5, 0.25, 0.125,... и представить его в двух формах: в виде суммы элементарных слагаемых и в виде аналитического выражения суммы членов убывающей геометрической прогрессии U(z) = a1=(1 q), где a1 = u(0) — первый член прогрессии, q — знаменатель прогрессии.
8.5.3.2. Вывести выражения для передаточных АЧХ и ФЧХ рекурсивного фильтра второго порядка, структурная схема которого представлена на рис. 8.107.
8.5.4. Вопросы для самопроверки
1.Что такое АЦП и ЦАП, какие функции они выполняют?
2.Что такое дискретизация аналогового сигнала во времени?
3.Что такое квантование сигнала по уровню?
4.Что такое шум квантования?
5.Как связано количество уровней квантования с разрядностью используемого двоичного кода?
6.Как связана относительная погрешность представления мгновенных значений сигнала двоичными кодовыми комбинациями с количеством уровней квантования и с разрядностью двоичного кода?
7.Как выбирается значение шага дискретизации?
8.Что такое z-преобразование?
9.Как получить z-образ числовой последовательности?
10.Что такое цифровая цепь?
11.Какие элементы могут содержаться в структурных схемах цифровых фильтров?
12.Что такое импульсная характеристика цифрового фильтра?
13.Какие типы цифровых фильтров Вам известны?
14.Чем отличаются друг от друга алгоритмы формирования выходных последовательностей в рекурсивных и трансверсальных цифровых фильтрах?
15.Чем отличаются структурные схемы рекурсивных цифровых фильтров от структурных схем трансверсальных фильтров?
16.Каково принципиальное отличие импульсных характеристик рекурсивных фильтров от импульсных характеристик трансверсальных фильтров?
17.В чём заключается простое правило z-преобразования линейных разностных уравнений?
18.Что такое системная функция цифрового фильтра и как получить её аналитическое выражение?
19.Чем отличаются друг от друга структуры аналитических выражений системных функций рекурсивного и трансверсального цифровых фильтров?
Частотная фильтрация электрических сигналов |
387 |
20.Как получить аналитическое выражение комплексной передаточной функции цифрового фильтра?
21.Чем отличаются друг от друга структуры аналитических выражений комплексных передаточных функций рекурсивного и трансверсального цифровых фильтров?
22.Как получить аналитические выражения передаточных АЧХ
иФЧХ цифрового фильтра?
23.В чём состоит принципиальное отличие передаточных АЧХ
иФЧХ цифровых фильтров от соответствующих характеристик аналоговых фильтров?
8.5.5.Задание для самостоятельного выполнения
экспериментов на персональном компьютере
8.5.5.1.Получить графики частотных характеристик рекурсивного фильтра первого порядка и убедиться в том, что эти характеристики имеют периодический характер. Показать, что в определённом диапазоне частот и при определённых сочетаниях значений коэффициентов исследуемый фильтр аналогичен по своим свойствам аналоговой RC-цепи с управляемой постоянной времени.
8.5.5.2.Получить графики частотных характеристик рекурсивного фильтра второго порядка и убедиться в том, что эти характеристики имеют периодический характер. Показать, что в определённом диапазоне частот и при определённых сочетаниях значений коэффициентов исследуемый фильтр аналогичен по своим свойствам последовательному колебательному контуру с управляемыми резонансной частотой и добротностью.
8.5.6. Порядок выполнения экспериментов
8.5.6.1.Получить при помощи Mathcad в диапазоне частот от 0 до 4 рад/с графики передаточной АЧХ в безразмерных единицах и
вдецибелах, график частотной характеристики ослабления в децибелах и график передаточной ФЧХ, а также график передаточной АЧХ
вбезразмерных единицах в диапазоне частот от 0 до 100 рад/с для рекурсивного фильтра первого порядка, структурная схема которого представлена на рис. 8.106,a, задав a = 0;2 и b = 0;8. На основании вида полученных графиков передаточной АЧХ в безразмерных единицах сделать и занести в отчёт вывод о том, что частотные характеристики цифрового фильтра простираются в беспредельном диапазоне частот и носят периодический характер.
8.5.6.2.Повторить эксперимент, описанный в п. 8.5.6.1, задав новые значения коэффициентов: a = 0;5 и b = 0;5.
8.5.6.3.Повторить эксперимент, описанный в п. 8.5.6.1, задав новые значения коэффициентов: a = 0;7 и b = 0;3. На основании результатов экспериментов, полученных при выполнении пп. 8.5.6.1–8.5.6.3,

388 Г л а в а 8
сделать и записать в отчёт вывод о том, что цифровой фильтр первого порядка в ограниченном диапазоне частот при определённых значения коэффициентов обладает частотными характеристиками, аналогичными характеристикам RC-цепи с различными значениями постоянной времени .
8.5.6.4. Повторить эксперимент, описанный в п. 8.5.6.1, для рекурсивного фильтра второго порядка, структурная схема которого представлена на рис. 8.107, задав a0 = 0;9, a1 = 0;1, b1 = 0;6, b2 = 0;6
изаменив диапазон частот 0...4 рад/с диапазоном 0...6 рад/с.
8.5.6.5.Повторить эксперимент, описанный в п. 8.5.6.1, для рекурсивного фильтра второго порядка, структурная схема которого
представлена на рис. 8.107, задав a0 = 0;95, a1 = 0;1, b1 = 0;8, b2 =
=0;6 и заменив диапазон частот 0...4 рад/с диапазоном 0...6 рад/с.
8.5.6.6.Повторить эксперимент, описанный в п. 8.5.6.1, для рекурсивного фильтра второго порядка, структурная схема которого представлена на рис. 8.107, задав a0 = 0;65, a1 = 0;1, b1 = 0;6, b2 =
=0;35 и заменив диапазон частот 0...4 рад/с диапазоном 0...6 рад/с. На основании результатов экспериментов, полученных при выполнении пп. 8.5.6.4–8.5.6.6, сделать и записать в отчёт вывод о том, что цифровые фильтры второго порядка в ограниченном диапазоне частот при определённых значениях коэффициентов обладает частотными характеристиками, аналогичными характеристикам последовательного колебательного контура с различными значениями резонансной частоты и добротности.
8.5.7. Методические указания
8.5.7.1.Выполнять эксперименты следует в системе Mathcad.
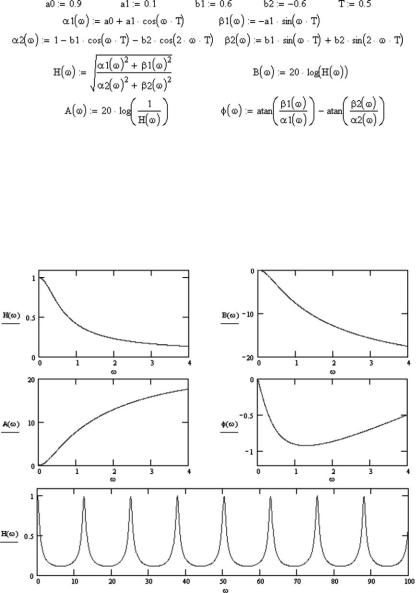
8.5.7.2.При выполнении заданий по пп. 8.5.6.1–8.5.6.3 удобно пользоваться следующей программой, построенной на основании выведенной ранее формулы (8.36):
Нужно устанавливать следующие диапазоны значений рассчитываемых величин на вертикальных осях получаемых графиков: для H(!) от 0 до 1,1, для B(!) от 20 до 0, для A(!) от 0 до 20, для φ(!) от 1,2 до 0.