TETs_Sobolev

Рис. 8.115. Зависимости, полученные по заданию в п. 8.5.6.6

8.6. Синтез цифровых фильтров

8.6.1. Цели изучения

1.Ознакомление с принципами формирования системных функций составных цифровых цепей.

2.Ознакомление с типовыми звеньями цифровых фильтров.

3.Ознакомление с принципами формирования нуль-полюсных диаграмм и с методом проверки цифровых фильтров на устойчивость их работы.

4.Ознакомление с методикой расчёта цифровых фильтров по рабочим параметрам.

8.6.2. Основные теоретические положения

8.6.2.1. Рассмотрим основные соединения цифровых цепей. При каскадном соединении цифровых цепей (рис. 8.116) их системные функции перемножаются:

H(z) = H1(z)H2(z) HK(z):

Следовательно, z-образ выходного сигнала определяется так:

Y (z) = X(z)H(z) = X(z)H1(z)H2(z) HK(z):

Рис. 8.116. Каскадное соединение цепей

Рис. 8.117. Параллельное соединение цепей

Рис. 8.118. Включение одной цепи в контур обратной связи другой цепи

При параллельном соединении цифровых цепей (рис. 8.117) их системные функции складываются:

H(z) = H1(z) + H2(z) + : : : + HK(z):

Следовательно, z-образ выходного сигнала определяется так:

Y (z) = X(z)H(z) = X(z)[H1(z) + H2(z) + : : : + HK(z)]:

При включении одной цифровой цепи в контур обратной связи другой цепи (рис. 8.118) общая системная функция определяется так:

H1(z)

H(z) = 1 H1(z)H2(z):

Следовательно, z-образ выходного сигнала определяется так:

H1(z)

Y (z) = X(z)H(z) = X(z)1 H1(Z)H2(z):

8.6.2.2. Пусть дана системная функция

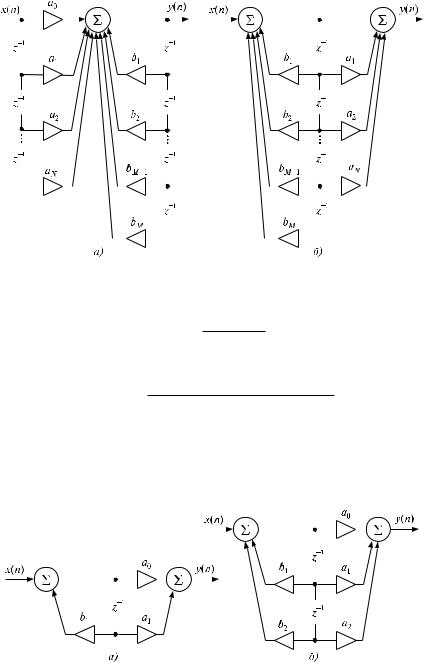
По этому выражению можно построить структурную схему, изображённую на рис. 8.119,a. Однако можно сначала провести рекурсивное преобразование сигнала, а затем трансверсальное:

т. е. построить схему согласно рис. 8.119,b. Последовательность обработки информации внутри фильтра будет другой, но результат фильтрации останется тем же, т. е. выходные сигналы у обеих схем будут одинаковыми при одинаковых входных сигналах. Первую схему будем называть классической, вторую — типовой. Последняя содержит два сумматора, но меньшее количество элементов задержки.

8.6.2.3. Обычно цифровые фильтры конструируются из типовых звеньев. Типовое звено первого порядка описывается системной

8.6.2.4. Свойства цифровой цепи полностью описываются её нульполюсной диаграммой. Построим такую диаграмму для цепи, структурная схема которой приведена на рис. 8.120,b, при следующих значениях коэффициентов: a0 = 1, a1 = 1, a2 = 0;5, b1 = 1;2, b2 = 0;45. Линейное разностное уравнение, описывающее закон функционирования соответствующей классической схемы, имеет вид

y(n) = 1x(n) 1x(n 1) + 0;5x(n 2) 1;2y(n 1) + 0;45y(n 2):

Приведённое линейное разностное уравнение имеет вид

воздействие вызывает на её выходе бесконечно нарастающий отклик, и наоборот: цепь является устойчивой, если ограниченный входной сигнал вызывает ограниченный выходной сигнал.

Подойдём к формулировке критерия устойчивости цифровой цепи на основании свойств системной функции.

Операторная передаточная функция аналоговой цепи H(p) является функцией комплексной переменной p = + j!. Системная функция цифровой цепи H(z) является функцией комплексной переменной z = x+jy. Значения переменных p и z отображаются в разных плоскостях: в p-плоскости и в z-плоскости.

Установим связь между точками этих плоскостей. Из сопоставления формулы z-преобразования (8.27) с формулой дискретного преобразования Лапласа следует, что

z = epT = e( +j!)T = e T ej!T = rej!T :

При = 0 имеем z = e0T ej!T = 1ej!T , т. е. r = 1. Следовательно, любая точка, расположенная на вертикальной оси (оси мнимых чисел) p-плоскости, отображается в z-плоскости на окружности с радиусом, равным единице, а сама ось отображается в виде единичной окружности (см. рис. 8.121), При < 0 имеем r < 1, а при > 0 имеем r > 1. Следовательно, любая точка, расположенная в левой полуплоскости p, отображается на z-плоскости внутри единичной окружности, а расположенная в правой полуплоскости p, отображается на z-плоскости вне единичной окружности (см. рис. 8.121).

Известно, что аналоговая цепь устойчива, если все полюсы (т. е. нули знаменателя) её передаточной функции H(p) расположены в левой полуплоскости. Поэтому, исходя из вышеизложенного, можно сформулировать критерий устойивости цифровой цепи следующим образом:

Цифровая цепь устойчива, если все полюсы (т. е.нули знаменателя) её системной функции H(z) расположены внутри единичной окружности.

Если хотя бы один полюс расположен вне единичной окружности, то цепь неустойчива.

Цепь, рассмотренная в предыдущем примере, неустойчива, так как один из её полюсов лежит вне единичной окружности (см. рис. 8.121). При других значениях коэффициентов эта цепь может оказаться устойчивой.

8.6.2.6. Рассмотрим примеры синтеза цифровых фильтров. Пример 1. Синтезировать цифровой фильтр нижних частот

Баттерворта, отвечающий следующим требованиям:частота дискретизации fд = 26 кГц;

верхняя граничная частота полосы пропускания fп = 2 кГц;

нижняя граничная частота полосы задерживания fз = 4;7 кГц;

максимальное ослабление в полосе пропускания Amax = 3 дБ;

минимальное ослабление в полосе задерживания Amin = 23 дБ.

Решение.

1. Рассчитываем период дискретизации:

T= 1=fд = 1=26000 = 3;846 10 5c = 38;46 мкс:

2.Рассчитываем угловые граничные частоты полос пропускания

изадерживания аналогового прототипа:

=3;32 104 рад=с:

3.Определим порядок фильтра:

сов, которые имеют отрицательную вещественную часть, т. е. располагаются в левой полуплоскости p. В данном примере это p2, p3 и p4.

398 Г л а в а 8

5. Найденные полюсы являются нулями знаменателя передаточной функции аналогового прототипа. Следовательно, аналитическое выражение упомянутого знаменателя выглядит так:

(p p2)(p p3)(p p4) = (p + 0;5 j0;866)(p + 1)(p + 0;5 + j0;866) = = (p + 1)[(p + 0;5)2 (j0;866)2] = (p + 1)(p2 + p + 0;25 + 0;75) =

= (p + 1)(1 + p + p2):

Записываем выражение передаточной функции аналогового прототипа проектируемого фильтра

1

H(p) = (1 + p)(1 + p + p2):

6. Для перехода от аналогового прототипа к требуемому цифровому фильтру применяем билинейное преобразование, т. е. выполняем

В результате получаем выражение системной функции требуемого цифрового фильтра

Приводим это выражение к стандартному виду. Для этого сначала приводим каждую скобку к общему знаменателю:

Переносим знаменатель знаменателя в числитель и раскрываем скобки в оставшемся знаменателе:

Раскрываем квадрат в числителе и группируем члены в скобках знаменателя:

(z + 1)(z2 + 2z + 1)

H(z) = [(B+1)z + 1 B][(B2 +B+1)z2 + (2 2B2)z + (B2 B + 1)]:

Нормализуем знаменатель, для чего выносим за скобки B + 1 в первом сомножителе знаменателя и B2 +B+1 во втором сомножителе

знаменателя, и записываем всё выражение в виде трёх сомножителей:

Делим числитель и знаменатель второго сомножителя на z, а третьего сомножителя на z2:

Подставив это значение B в предыдущее выражение для H(z), получим окончательное выражение для системной функции требуемого цифрового фильтра:

Вышеприведённые выкладки можно упростить, прибегнув к помощи системы Mathcad:

В выражении для расчёта переменной p была произведена замена z на 1=a. Теперь следует вернуться к переменной z, подставив в последнюю формулу z 1 вместо переменой a, а также с целью нормализации полученного выражения разделить первую скобку знаменателя на константу 5;06 1019, вторую скобку знаменателя на константу 2;15 1020, а числитель на произведение этих констант. В результате получим следующее выражение для системной функции проектируемого фильтра: