TETs_Sobolev

Предисловие

Дисциплина «Теория электрических цепей» призвана сформировать те базовые знания, которые в дальнейшем будут использованы студентами, обучающимися по различным электротехническим и радиотехническим специальностям, в процессе освоения многих последующих специальных дисциплин. Не менее важным является привитие навыков применения современных вычислительных средств при исследовании, анализе и синтезе различных электрических схем и устройств.

Данная книга сочетает в себе качества традиционного учебника и описания самостоятельных исследований, выполняемых в домашних условиях на ПК или в компьютерных классах. Это стимулирует активную работу с книгой и пробуждает у студента чувство сопричастности к изучаемым явлениям. Материал предъявляется дозировано, каждый пункт в описании подчинён одной главной мысли. Поэтому изучение не следует прерывать, не проработав начатый пункт до конца. Книга обеспечивает многоплановость её использования: от ознакомления с основными теоретическими положениями, подкреплёнными соответствующими примерами расчёта, до подробной проработки содержания курса с составлением отчёта о изученном материале и выполненных экспериментах. В последнем случае отчет по каждому параграфу должен содержать как минимум следующее:

название работы;

формулировку цели работы;

формулы (с пояснениями), графики и таблицы рассчитанных величин, полученные в процессе предварительной подготовки;

вопросы для самопроверки и краткие ответы на них;

схемы, использованные в процессе выполнения экспериментов на персональном компьютере;

значения, полученные в процессе обработки результатов компьютерных экспериментов;

графики, отражающие частотные или временные´ зависимости величин, полученные в процессе компьютерных экспериментов;

выводы по результатам экспериментов для каждого пункта исследований.

Перед выполнением экспериментальной части каждой работы необходимо внимательно ознакомиться с соответствующими методическими указаниями.

При написании данной книги автор исходил из предположения, что студенты знакомы с широко распространённой системой Mathcad из курса «Информатика». Поэтому здесь описываются приёмы управления только системой схемотехнического моделирования MicroCap, причём соответствующий материал предъявляется постепенно на протяжении всей книги и только в том объёме, который диктуется текущей необходимостью.

Предлагаемое учебное пособие может быть использовано при любой форме обучения (дневное, заочное, дистанционное). Книга может рассматриваться и как расширенное описание лабораторного практикума по дисциплине ТЭЦ.

C и индуктивностью L. Однако эти элементы конструктивно выполняются так, чтобы один из перечисленных параметров имел большое значение, а остальные (называемые паразитными параметрами) — малое. Поэтому влиянием паразитных параметров на низких и средних частотах можно пренебречь. На этом основании в теории электрических цепей рассматриваются идеализированные пассивные элементы. Они часто называются по их основному параметру: резистивное сопротивление, ёмкость, индуктивность. Их условные графические обозначения приведены на рис. 1.1.

Втех случаях, когда всё же необходимо учитывать влияние паразитных параметров, их отражают в схеме включением соответствующих дополнительных идеализированных элементов. Например, на сверхвысоких частотах электрическая модель резистора может быть такой, как показано на рис. 1.2, где Lп и Cп — дополнительно включённые элементы.

Пассивные элементы делятся на неэнергоёмкие (R) и энергоёмкие (C и L). Действительно, в резистивных сопротивлениях электрическая энергия переходит в тепловую и не возвращается в схему.

Вемкостных и индуктивных элементах энергия накапливается в электрических и магнитных полях (соответственно) и при определённых обстоятельствах может возвращаться в электрическую цепь.

Втабл. 1.1 приведены известные из курса физики соотношения между электрическими величинами для линейных идеализированных элементов. Здесь и далее строчными буквами обозначены переменные во времени напряжения, токи и мощности, а прописными буквами — постоянные величины: u, U — напряжения; i, I — токи; p, P — мощности; w, W — энергии; T — интервал времени; индексом 0 отмечены начальные значения величин.

1.1.2.3. Кроме рассмотренных линейных пассивных элементов существуют нелинейные элементы (НЭ), напряжение на полюсах (клеммах, зажимах) которых связано нелинейной зависимостью с током, протекающим через них. График этой зависимости, т. е. вольт-ампер- ной характеристики (ВАХ), у НЭ имеет вид не прямой линии, как у линейного элемента, а кривой или ломаной линии. Нелинейный элемент можно определить как элемент, значение основного параметра которого (R, L или C) зависит от приложенного к нему напряжения

или протекающего по нему тока. Условные графические обозначения и соотношения токов и напряжений на полюсах НЭ приведены

втабл. 1.2.

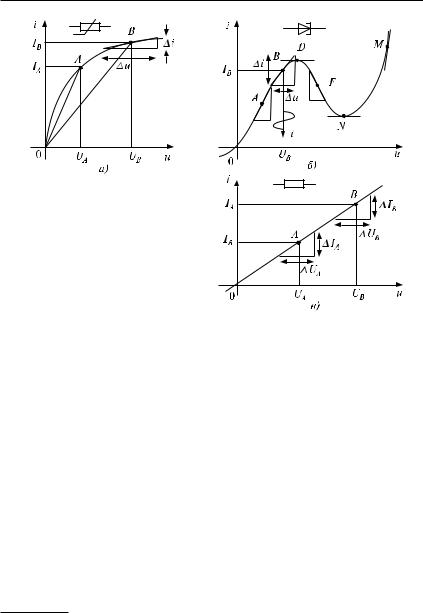
Вкачестве примера на рис. 1.3 представлены вольт-амперные характеристики некоторого нелинейного резистора (a), туннельного диода (b) и линейного резистора (v).

У нелинейного резистивного элемента различают статическое и динамическое (дифференциальное) сопротивление.

Статическое сопротивление НЭ (сопротивление постоянному току) пропорционально котангенсу угла наклона прямой, проходящей через данную точку графика ВАХ и начало координат. В разных точках ВАХ оно имеет разные значения (см. рис. 1.3,a, где RA = UA=IA,

RB = UB=IB, RA ≠ RB).

Дифференциальное сопротивление НЭ (сопротивление переменному току) du=di пропорционально котангенсу угла наклона касательной к графику ВАХ в заданной точке. В разных точках ВАХ не-

Рис. 1.3. Вольт-амперные характеристики пассивных элементов

линейного элемента оно также имеет разные значения (см. рис. 1.3,a, где rA = ∆uA=∆iA, rB = ∆uB=∆iB; rB > rA, а также рис. 1.3,b, где rA = ∆uA=∆iA, rB = ∆uB=∆iB, rB > rA, rD = rN = 1, rF < 0, rM 0).

Статическое и дифференциальное сопротивления НЭ в одной и той же точке ВАХ также имеют разные значения (см. построение для точки B на рис. 1.3,a).

У линейного элемента статическое и дифференциальное сопротивления равны и во всех точках ВАХ имеют одинаковые значения: RA = RB = rA = rB = R (на рис. 1.3,v все треугольники подобны).

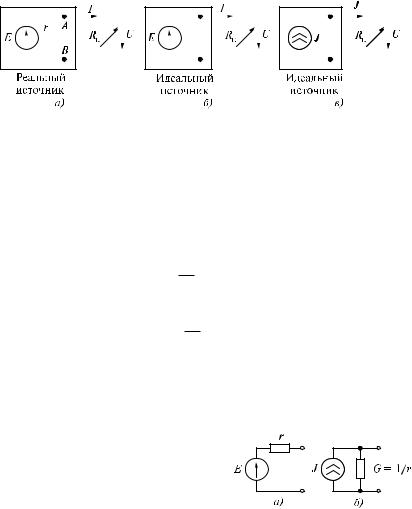
1.1.2.4. У реального источника электрической энергии (рис. 1.4,a) напряжение U между его полюсами A и B и ток I через нагрузку зависят от сопротивления нагрузки Rн . Действительно, для цепи,

Одновременная зависимость и тока, и напряжения от нагрузочного

Стрелка на символе резистора означает, что допускается плавное изменение его сопротивления.

Здесь и далее var означает изменение соответствующей величины (I или U) при изменении нагрузочного сопротивления Rн, а const — независимость соответствующей величины от Rн.

Рис. 1.4. Реальный источник (a) и идеальные источники (b, v) электрической энергии

сопротивления объясняется наличием конечного внутреннего сопротивления источника r. В теории электрических цепей введены понятия идеальных источников: источника напряжения и источника тока.

У источника напряжения внутреннее сопротивление r равно нулю, поэтому он обеспечивает на нагрузочном элементе Rн напряжение U, значение которого не зависит от Rн и всегда равно ЭДС (рис. 1.4,b):

E

U = IRн = Rн Rн = E = const :

Однако ток I в полной мере зависит от сопротивления нагрузки:

I = E = var : Rн

У источника тока внутреннее сопротивление равно бесконечности, и поэтому этот источник обеспечивает в той ветви, где он расположен, ток, независящий от внешнего сопротивления Rн (рис. 1.4,v): J = const. Однако напряжение между его полюсами зависит от сопротивления нагрузки: U = JRн = var.

Модель реального источника

можно представить либо в виде источника напряжения, последовательно с которым включено резистивное

сопротивление (рис. 1.5,a), либо в виде источника тока, параллельно с которым включено то же самое сопро-

тивление (рис. 1.5,b). Можно показать, что схему с источником напряжения (рис. 1.5,a) несложно преобразовать в эквивалентную ей схему с источником тока (рис. 1.5,b) и наоборот, использовав соотношения J = E=r или E = Jr. При этом, как отмечено ранее, сопротивления r в обеих схемах имеют одно и то же значение.

Из соотношений (1.1) следует, что

при Rн = 0 имеем U = 0 и I = E=r;

при Rн = 1 имеем U = E и I = 0;

величины U и I связаны линейной зависимостью.