Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3750

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

13.52 Mб

Скачать

☆

1 / 211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

ФГБОУ ВПО «Воронежский государственный технический университет»

В.В. Дежин С.А. Кострюков

ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ИХ ПРИМЕНЕНИЕ ПРИ ФИЗИКОМАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

Воронеж 2015

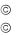
УДК 517

Дѐжин В.В. Функции комплексного переменного и их применение при физико-математическом моделировании: учеб. пособие [Электронный ресурс]. – Электрон. текстовые, граф. данные (12,8 Мб)/ В.В. Дежин, С.А. Кострюков. – Воронеж : ФГБОУ ВПО «Воронежский государственный технический университет», 2015. – 1 электрон. опт. диск (CD-ROM). – Систем. требования: ПК 500 и выше; 512 Мб ОЗУ; Windows XP/7/8; Adobe Reader 9 или более поздняя версия; 1024x768; CD-ROM; мышь. – Загл. с экрана.

Пособие содержит теоретический материал по функциям комплексного переменного, примеры решения задач, а также прикладные задачи технической физики.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлениям 150100.62 «Материаловедение и технологии материалов», 223200.62 «Техническая физика», 222900.62 «Нанотехнологии и микросистемная техника», всем профилям, дисциплинам «Математика» и «Специальные главы математики».

Ил. 55. Библиогр.: 33 назв.

Рецензенты: кафедра математических методов исследования операций Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. А.Г. Баскаков); канд. физ.-мат. наук, доц. В.В. Ломакин

Дѐжин В.В., Кострюков С.А., 2015 Оформление. ФГБОУ ВПО «Воронежский государственный технический университет», 2015

ВВЕДЕНИЕ

Раздел «Функции комплексного переменного» является одним из наиболее важных и сложных при изучении курса «Специальные главы математики». Глубокое неформальное изучение таких основных понятий как комплексные числа, кривые и области на комплексной плоскости, основные элементарные функции комплексного переменного, дифференцирование функций комплексного переменного, интегрирование функций комплексного переменного, разложение функций комплексного переменного в ряды Лорана, применение вычетов к вычислению контурных интегралов и определенных интегралов необходимо при усвоении специальных курсов для студентов материаловедческих специальностей.

В главе 1 пособия содержатся необходимые теоретические сведения по комплексным числам и действиям с ними. Во 2-й главе пособия определяются основные элементарные функции комплексного переменного, вводится понятие аналитических функций комплексного переменного и их дифференцирования. В 3-й главе пособия излагается понятие интегрирования функций комплексного переменного, применение интегральной формулы Коши. В 4-й главе пособия изучается разложение функций комплексного переменного в ряды Лорана. Проводится классификация изолированных особых точек, определяется вычисление вычетов в изолированных особых точках. В 5-й главе рассматриваются вычеты и их приложение к вычислению интегралов. Главы разбиты на параграфы, в каждом из которых приведены примеры решения задач. В 6-й главе приведены примеры физико-математического моделирования задач физики твердого тела и технической физики. В приложениях даны понятия однолистностных функций и конформных отображений.

Пособие может использоваться как студентами, так и преподавателями для подготовки к практическим занятиям, контрольным работам, коллоквиуму, экзамену.

ГЛАВА 1

КОМПЛЕКСНЫЕ ЧИСЛА. КОМПЛЕКСНАЯ ПЛОСКОСТЬ

1.1. Определение комплексного числа

Комплексными числами называются пары x, y действительных чисел x и y , если для них определены понятия ра-

венства и операции сложения и умножения следующим образом:

1. Два комплексных числа x1, y1 и x2 , y2 считаются

равными тогда и только тогда, когда
			x1	x2 и	y1	y2 .		(1.1)
2.	Суммой двух комплексных чисел x1,						y1 и	x2 ,	y2
называется комплексное число
				x1 x2 ,	y1	y2		(1.2)
3. Произведением двух комплексных чисел								x1, y1	и
x2 , y2	называется комплексное число
			x1x2	y1 y2 ,	x1 y2	x2 y1 .		(1.3)
Из формул (1.2) и (1.3) вытекают соотношения:
x1, 0		x2 , 0	x1	x2 , 0 ,	x1, 0 x2 , 0		x1x2 , 0 ,

которые показывают, что операции над комплексными числа-


ми вида	x, 0 совпадают с операциями над действительными
числами	x . Поэтому комплексные числа вида x, 0			отождест-
вляются с действительными числами:			x, 0 x .
Комплексное число 0, 1			называется мнимой еди-
		1
ницей и обозначается буквой i , т.е. i			0, 1 . Для произведения
i2 по формуле (1.3) имеем i2 i i		0, 1 0, 1		1, 0	1.

Из формул (1.2) и (1.3) вытекают также равенства:

0, y	0, 1	y, 0	iy ,
x, y	x, 0	0, y	x iy .

Таким образом, каждое комплексное число x, y можно представить в виде x iy . Запись комплексного числа в виде x iy называется алгебраической формой комплексного числа Комплексные числа вида iy называются чисто мнимыми. В частности, число 0, т.е. комплексное число 0, 0 , является единст-

венным числом, которое одновременно и действительное и чисто мнимой.

С помощью алгебраической формы комплексного числа

формулы (1)–(3) записываются таким образом:

iy1

iy2 тогда и только тогда, когда

x2 и

y2 .

(1.4)

x1, y1

+ x2 , y2

i y1

y2 .

(1.5)

iy1

iy2

x1x2

y1 y2

i x1 y2

x2 y1 .

(1.6)

Комплексное число x

принято обозначать одной бук-

вой z , т.е.

z x

iy . Число

называется действительной ча-

стью,

число

–

мнимой

частью

комплексного

числа

z x

iy . Для этих чисел приняты обозначения:

Re x

Re z ,

Im x

Im z .

(Обозначения Re и Im являются сокращениями французских слов Réel (действительный) и Imaginaire (мнимый)). Здесь, как

и всюду в дальнейшем, предполагается, что x и				y – действи-
тельные числа.
Комплексное число	x	iy	называется комплексно сопря-
жѐнным с числом x iy и обозначается:
			x iy .	.(1.7)
z	x	iy

Равенство z z имеет место в том и только в том случае, когда z – действительное число.

Пример 1.1. z 5 3i , тогда z 5 3i .

Число x2 y2

называется модулем комплексного числа

iy и обозначается

y2 .

(1.8)

Очевидно,

0 ,

причем

тогда и только тогда,

когда

0 . Отметим две формулы

(1.9)

2 ,

(1.10)

которые вытекают из равенств (1.7), (1.8) и равенства

x iy x iy

y2 .

Пример 1.2.

3i ,

тогда

(

3)2

9i2

34 , zz

3i)(5

3i)

15i

34 .

Операции сложения и умножения комплексных чисел обладают следующими свойствами:

1. Коммутативность

	z1	z2	z2	z1 ,	z1z2	z2 z1 .
2. Ассоциативность
z1 z2	z3	z1	z2	z3 ,	z1z2 z3 z1 z2 z3 .
3 Дистрибутивность
		z1 z2	z3	z1z2 z1z3 .
Докажем, например, коммутативность сложения. Пусть
z1 x1 iy1 , z2	x2	iy2 . Тогда по формуле (1.5) имеем
	z1	z2	x1	x2	i y1	y2 ,
	z2	z1	x2	x1	i y2	y1 .

Но по свойству коммутативности сложения действительных

чисел	x1	x2 x2 x1 и y1 y2 y2 y1 . Следовательно,
z1 z2	z2	z1 . Аналогично проверяются остальные свойства.

Из свойств 1-3 вытекает, что операции сложения и умножения над комплексными числами x iy обладают фор-

мально такими же свойствами, как если бы число i было действительным. В частности, нет необходимости запоминать формулы (1.5)–(1.6), их можно получить по обычным формулам алгебры. Например, (1.6) вытекает из равенства

x iy		x	iy	x x		iy y		ix y i2 y y			2
1	1	2	2	1	2	1	2	2	1	1	2

и равенства i2 1 . Числа нуль и единица в множестве комплексных чисел обладают теми же свойствами, что и в множестве действительных чисел. А именно, для любого комплексного числа z имеют место равенства

z 0 z , z 1 z .

В множестве комплексных чисел можно ввести операцию, обратную к операции сложения. Эта операция, как обычно, называется вычитанием. Для любых двух комплексных чи-

сел	z1 и z2 существует,		и притом только одно, число z , удов-
летворяющее уравнению
			z	z2	z1 .					(1.11)
Это число называется разностью чисел							z1 и z2 и обозначается
z1	z2 . В частности, разность 0				z обозначается				z .
	Из равенств (1.4) и (1.5) вытекает, что для любых ком-
плексных чисел z1		x1	iy1	и	z2	x2	iy2	уравнение		(1.11)
имеет единственное решение					z	x1	x2	i y1	y2 .	Таким
образом,
	z1	z2	x1	x2	i	y1	y2 .			(1.12)
	Операция, обратная умножению, называется делением, а
частным двух комплексных чисел						z1	и z2	называется такое
число z , которое удовлетворяет уравнению
			zz2		z1 ,					(1.13)
и обозначается z1 : z2 или z1				z2 . Докажем, что уравнение (1.13)

имеет единственное реше6ние для любых комплексных чисел

и z2 , если z2

0 . Умножая обе части уравнения (1.13) на

число

и используя формулу (1.10), получаем

z z

откуда умножением на число 1

2 находим z

z1z2

. Таким

образом,

z1z2

0 .

(1.14)

z2 z2

Если z1

iy1

и z2

iy2 , то формулу (1.14) можно запи-

сать в виде:

x iy

iy1

iy2

x x

y y

x y x y

1 2

2 1

1 2

iy2

x22

y22

x22

y22

Пример 1.3. Пусть z1

3i , z2

4i .Тогда:

z1 z2

(2 3) i( 3 4) 5 i ,

(2 3) i( 3 4)

1 7i ,

z z

2 3i 3 4i

6 8i 9i 12i2

6 i 12 18 i ,

2 3i

2 3i 3 4i

6 8i 9i 12i2

6 17

i .

3 4i

3 4i 3 4i

1.2. Геометрическая интерпретация комплексного числа

Пусть на плоскости задана прямоугольная система коор-

динат.

Комплексное число

изображается точкой

плоскости с координатами

, и эта точка обозначается той

же буквой z (рис. 1.1). Такое соответствие между комплексными числами и точками плоскости является взаимно однозначным. При этом действительные числа изображаются точками оси абсцисс, а чисто мнимые числа изображаются точками оси ординат. Поэтому ось абсцисс называется действительной осью, а ось ординат – мнимой осью. Плоскость, на которой изображаются комплексные числа, называется ком-

плексной плоскостью. Ясно, то точки z	и	z	симметричны
относительно начала координат, а точки	z и	z	симметричны

относительно действительной оси (рис. 1.1). Комплексное число z изображается также вектором с началом в точке 0 и концом в точке z (рис. 1.1).Такое соответствие между комплексными числами и векторами комплексной плоскости также является взаимно однозначным. Поэтому вектор, изображающий комплексное число z , означается той же буквой z . Из форму-

лы (1.8) и рис.1.1 видно, что длина вектора

z равна

и име-

ют место неравенства

Re z

Im z

-z

z=x+iy

-x				x

-z

-y

Рис. 1.1

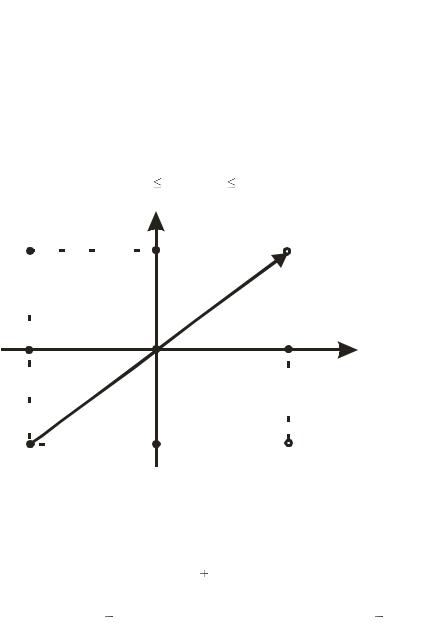
С помощью векторной интерпретации наглядно иллюстрируются сложение и вычитание комплексных чисел. Из формулы (1.5) вытекает, что число z1 z2 изображается вектором,

построенным по обычному правилу сложения векторов	z1	и z2
(рис. 1.2). Вектор z1 z2 строится как сумм векторов z1	и	z2

(рис. 1.2). Из рис. 1.2 видно, что расстояние между точками

z1 и z2 равно длине вектора z1

z2 , т.е. равно

z1+z2

z1- z2

-z2

Рис. 1.2

Пример

1.4.

Множество

точек

z ,

удовлетворяющих

уравнению

R , есть окружность радиуса

R с центром

в точке z0 , так как

– расстояние между точками z и z0

Пример

1.5.

Множество

точек

z ,

удовлетворяющих

уравнению

, есть множество точек, равноуда-

ленных от точек z1

z2 . Следовательно,

это уравнение пря-

мой, перпендикулярной отрезку, соединяющему точки z1 и z2 , и проведенной через его середину.

Пример

1.6.

Множество

точек

z ,

удовлетворяющих

уравнению

2a ,

где a

, есть эллипс с

фокусами в точках

z1 ,

и с большей полуосью, равной a , так

1 / 211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.202212.74 Mб43733.pdf
#
15.11.202212.79 Mб13734.pdf
#
15.11.202213.19 Mб03742.pdf
#
15.11.202213.22 Mб03744.pdf
#
15.11.202213.44 Mб03749.pdf
#
15.11.202213.52 Mб03750.pdf
#
15.11.202213.78 Mб23756.pdf
#
15.11.202213.84 Mб03757.pdf
#
15.11.202214.07 Mб13760.pdf
#
15.11.202214.09 Mб03762.pdf
#
15.11.202214.86 Mб43773.pdf