Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Функции комплексного переменного и их применение при физико-математическом моделировании. Дежин В.В., Кострюков С.А

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

13.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 217 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>


n	0	0 , n		, т.е.	различные ветви функции в этих точках
совпадают.
		Для	логарифмической			функции w Ln z	точками раз-
ветвления являются z					0 и z	, причем Ln 0	и Ln

. Любое конечное число обходов (в одном и том же направлении) вокруг точки z 0 не приведет к первоначальной ветви функции w Ln z . Такие точки ветвления называются лога-

рифмическими.

При интегрировании необходимо выделять ветвь многозначной функции. Это достигается заданием значения многозначной функции в некоторой точке кривой интегрирования.

Если контур интегрирования замкнут, то начальной точкой z0 пути интегрирования считается та точка, в которой за-

дано значение подынтегральной функции.

Пример 6. Вычислить интеграл

, где C – верхняя

дуга окружности

1, интегрирование проводится в положи-

тельном направлении. Для функции

берется та ветвь, для

которой

Решение. Первый способ. Функция

имеет два значе-

ния (

arg z ):

cos

i sin

cos

i sin

cos

i sin

Так как интегрирование ведется по дуге окружности

1, то

cos

i sin

cos

i sin

(*)

Условию

1 удовлетворяет второе значение (*). В самом

деле,

пусть

тогда

arg z

i sin 0

cos 0

Применяя формулу Ньютона-Лейбница, получим

1 dz

1 .

Полагая в формуле (*) z

1, найдем

cos

arg(

i sin

arg(

cos

i sin

i .

Согласно выбору ветви имеем

1 и окончательно полу-

чим

2i .

Второй способ. Полагаем z

rei

, где r

1, а ме-

няется от

до

Из условия

следует,

что

. Тогда

0 e

2ei

e i

2 e

2 i 1 2 2i .

ln3 z

Пример 7. Вычислить интеграл

по дуге окруж-

ности

1 ( ln z

– главное значение логарифма, ln1 0 ).

Решение. Первый способ. Применяя формулу НьютонаЛейбница, получим

						i	ln3 z	dz			i	ln3 z d ln z									ln4 z				i
							ln3 z				i										ln4 z				i

					1		z				1											4			1
					1						1											4			1
							ln4 i			ln4 1 ln4 i								1				4				4
							ln4 i			ln4 1 ln4 i								1	i							4		.
																			i									.
							4							4				4	2					64
	Второй способ. Делаем замену																				переменной												ln z w ,
dw	dz
	dz	. Дуга окружности											z		1 переходит в отрезок мнимой
	z	. Дуга окружности											z		1 переходит в отрезок мнимой
	z																									0,
оси, заключенный между точками																			0, 0				и								.		Интеграл
оси, заключенный между точками																			0, 0				и						2		.		Интеграл
примет вид
			i ln3 z				i			2	w3dw				w4		i		2	1 (i )4											4
			i ln3 z				i			2					w4		i		2	1 (i )4											4
							dz																									.
		1			z		dz		0					4			0			4		24								64		.
	Третий способ. Полагаем z																		rei	,			где										1. Тогда
	Третий способ. Полагаем z																		rei	,			где				r				z		1. Тогда
ln z	i	, dz				iei d . Действительная переменная																											изменяет-
ся в пределах 0											2 . В этом случае получаем
	i			3			2			3	3	i						2						4			2						4
																											2

			ln		z	dz			i		ie		d						3d															.
	1		z			dz	0				ei					0			3d					4			0				64			.
			z								ei													4							64

3.3. Интегральная формула Коши

Если функция f z аналитична в области D , z0 D и D – контур, охватывающий точку z0 , то справедлива ин-

тегральная формула Коши:

f	z0	1	f	z	dz .	(3.21)

		2 i	z	z0

При этом функция f	z имеет всюду в D производные любо-

го порядка, для которых справедливы формулы:

f n z0	n!	f	z		dz, n 1, 2, .	(3.22)

	2 i	z	z0	n 1

Формулами (3.21) и (3.22) применяются для вычисления некоторых интегралов.

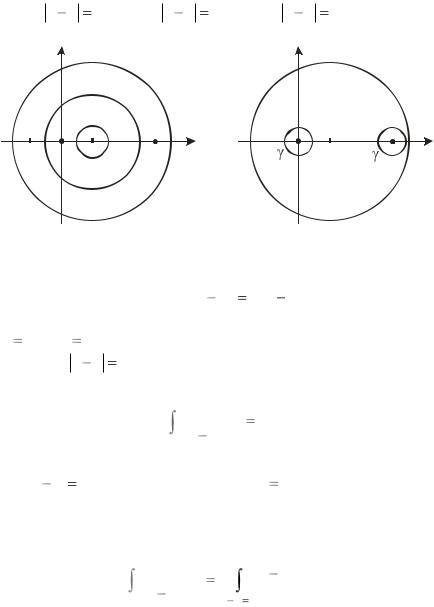
Пример 8. Вычислить dz , где C – окружность:

C z 3

а) z 2 , б) z 4 .

y	y
y
	\|
	z
	\|=
	2

| z | = 4

| z | = 3

		x	z0=0
z0=-3 0	x z0=-3 0	x	x

а)		б)
Рис. 3.4		Рис. 3.5
Решение. а) Если C – окружность радиуса 2, то подын-
тегральная функция	ez	является аналитической в каждой
тегральная функция	z 3	является аналитической в каждой
	z 3

точке круга	z	2 (рис. 3.4, а). Поэтому, в силу теоремы Коши
					ez
(3.17), получаем						dz 0 .
(3.17), получаем			z	2	z 3	dz 0 .
			z	2	z 3
б) Если C – окружность радиуса 4, то точка z0							3 (в

ней подынтегральная функция не определена) расположена

внутри окружности

4 (рис. 3.4, б).

Представим подынте-

гральную функцию в виде

, где f

является ана-

литической в каждой точке круга

4 . Применяя интеграль-

ную формулу Коши (3.21), получим

2 i ez

Пример 9. Вычислить

cos z

dz , где C :

3 .

Решение. Подынтегральная функция

cos z

является ана-

литической в круге

3 всюду кроме точки z0

0 (рис. 3.5).

Выделим под знаком интеграла функцию f

cos z , являю-

щуюся аналитической

круге

3 .

Воспользуемся инте-

гральной формулой Коши для производной (3.22). При z0 0 и n 2 получим

cos z

2 i

cos z

i .

z 0

		ez2
Пример 10. Вычислить интеграл				dz , если:
		z2
	C		6z

1) C1 : z 2 1; 2) C2 : z 2 3 ; 3) C3 : z 2 5 .

	y			y
	3				3
	2
	1
-3 -2 -1	1 2 3 5 6 7 x	-3	1	2	6 7 x
			1		2

а)	б)
Рис. 3.6
Решение. 1) Так как z2 6z z z	6 , поэтому знамена-

тель подынтегральной функции обращается в нуль в точках z 0 и z 6 . В замкнутой области, ограниченной окружностью C1 : z 2 1, подынтегральная функция аналитическая

(рис. 3.6, а), поэтому в силу теоремы Коши (3.17)

			ez2			0 .
					dz
			z2		dz
		C	z2	6z
		1
2)		Внутри области,			ограниченной окружностью
		3 , находится одна точка				z 0 , в которой знамена-
C2 :	z 2	3 , находится одна точка				z 0 , в которой знамена-

тель подынтегральной функции обращается в нуль (рис. 3.6, а). Перепишем интеграл в виде

		ez2					ez2
							z	6	dz .
				dz
		z2
C	2		6z		z 2	3		z

ez2

Функция

является аналитической в данной облас-

ти. Применяя интегральную формулу Коши (3.21), получим

ez2

z 6

dz 2 i

2 i

z 6

3) В области, ограниченной окружностью C3 : z 2 5 ,

имеем две точки z 0 и z 6 , в которых знаменатель подынтегральной функции обращается в нуль (рис. 3.6, а). Непосредственно формулу (3.21) применять нельзя. В этом случае для вычисления интеграла можно поступить так.

Первый способ. Разложим дробь

на простейшие:

6z 6

z 6

Подставив в интеграл, по формуле (3.21) получим

ez2

ez2 dz 1

ez2 dz

C z2

5 z 6 6

5 z

z 2

	1			1				ie36		i			e36	1
		2 iez2			2 iez2						i				.
6			z 6	6		z	0	3	3				3


Второй способ. Построим окружности											1	и	2	с центра-

ми в точках z 0 и				z	6 достаточно малых радиусов таких,

чтобы окружности не пересекались и целиком лежали в круге z 2 5 (рис. 3.6, б). В трехсвязной области, ограниченной

окружностями z 2 5, 1 и 2 , подынтегральная функция

всюду аналитична. По теореме Коши для многосвязной области (3.20) получаем

		ez2			ez2 dz		ez2 dz		.
				dz
		z2		dz	z2 6z		z2
z 2	5		6z					6z
			6z					6z
			1			2

К каждому интегралу в правой части можно применить интегральную формулу Коши (3.21). В результате получим

ez2

e36 1

dz 2 i

2 i

z 2

z2 6z

z 6

Пример 11. Вычислить интеграл

sin

dz .

1 2

-1

Рис. 3.7

Решение. Подынтегральная функция

sin

яв-

z 1 2

ляется аналитической в области

z 1

1 всюду, кроме точки

z 1 (рис. 3.7). Выделим под знаком интеграла функцию f

, являющуюся аналитической в круге

sin

sin z

1 2

z 1 2 z 1 2

z 1 2

Полагая в формуле (3.22) n

1 ,

1, получим

dz 2 if 1 .

z 1

1 z 1 2

Находим производную

sin

cos

z z

2 sin

z 1

1 3

Отсюда f

cos

. Следовательно,

sin

2 i

1 2

z 1

Пример 12. Вычислить интеграл

ch z dz

2 z

1 3

z 1

				1		2
-2	-1	1	2 x -2	-1	1	2 x

а) б)

Рис. 3.8

Решение. Первый способ. Знаменатель подынтегральной функции обращается в нуль в двух точках z1 1 и z2 1 , ле-

жащих внутри круга z 2 (рис. 3.8, а). Разложим на простейшие дроби функцию

1							1				1		1					1		1					1					1		1	.

	z 1 3 z 1								8 z 1 8 z 1 4 z 1 2																					2		z 1 3
Используя линейность интеграла, получим
				ch z dz									1						ch z						1						ch z
																z	2						dz				z	2				dz
		z	2 z 1 3 z 1											8					z 1							8					z 1
		z	2 z 1 3 z 1											8					z 1							8					z 1
1												ch z								1					ch z
															dz						z	2							dz .
					4	z		2		z 1 2					dz					2				z 1 3
					4	z		2		z 1 2										2				z 1 3

К первым двум интегралам применяем интегральную формулу Коши (3.21):

		ch z	dz 2 i ch1 ,			ch z	dz 2 i ch ( 1) 2 i ch1 .
z	2 z 1		dz 2 i ch1 ,	z	2 z 1		dz 2 i ch ( 1) 2 i ch1 .

Третий и четвертый интегралы вычисляем с помощью форму-

лы (3.22):

							ch z
							ch z
										dz		2	i	ch z			2					i sh1,
							z	1	2	dz		2	i	ch z		z	2					i sh1,
			z	2			z	1									1
							ch z					2	i				1				i ch1.
											dz			ch z



				z	2 z			1 3				2!						z 1


Окончательно получим
						ch z dz						2	i ch1		2			i ch1				2 i sh1

	z	2 z			1 3				z		1		8				8						4
	z	2 z			1 3				z		1		8				8						4
									i ch1			i	sh1		ch1			i		.

									2					2					2e
Второй способ. Построим окружности																					1		и	2	с центра-
																					1			2
ми в точках z1							1 и z2					1 достаточно малых радиусов таких,

чтобы окружности не пересекались и целиком лежали в круге z 2 (рис. 3.8, б). В трехсвязной области, ограниченной ок-

<<< < Предыдущая 1 2 3 4 5 67 / 217 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]