
3750
.pdf
а) |
б) |
в)
Рис. 6.13
Граница круга состоит из линий тока. Поэтому линия тока, приходящая в точку z2 , разветвляется на две – на верхнюю
и нижнюю дуги окружности (рис. 6.13, а). Точка z2 называется точкой разветвления. Во второй критической точке z1 линии тока (дуги окружности) снова сходятся; эта точка называется точкой схода. Заметим, что линия тока, входящая в точку z2 , и линия тока, выходящая из точки z1 , ортогональны к окружности. Действительно, в точке z1 имеем
f z1 |
0 , |
|
|
|
|
1 |
|
2V R2 |
0 . |
|
f |
z1 |
|
|
|
|
|
i |
|||
|
|
z2 |
|
|||||||
|
|
|
|
2 |
|
z1 |
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
При критическом значении |
|
|
0 имеем |
|
||||||
z1,2 |
iR , |
f |
|
iR |
0 , |
|
f iR |
0 , |
||
171

и потому угол между двумя соседними линиями тока, входя-
щими в точку z1,2 |
iR , равен |
3 (рис. 6.13, б). |
|
|
|||||||||||||||||||||
Если |
|
|
|
|
|
|
0 , то подкоренное выражение в (6.57) отрица- |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельно и |
|
z |
|
|
|
2 |
16 |
|
|
2V 2 R2 |
R . Из (6.56) сле- |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1,2 |
|
|
|
4 V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
дует, что |
|
z z |
2 |
|
R2 , |
так что одна критическая точка лежит |
|||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
внутри, а вторая – вне окружности |
|
z |
|
R . В этом случае появ- |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
ляются замкнутые линии тока (рис. 6.13, в). |
|
|
|
|
|||||||||||||||||||||
Циркуляцию |
|
можно выразить через координаты точки |
|||||||||||||||||||||||
схода: |
4 |
|
v |
R sin |
. Если же argV 0 , то |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 v R sin( |
) . |
|
|
|
|
(6.58) |
|||||||||
Пусть контур |
S – эллипс |
|
x2 |
|
|
|
|
y2 |
|
1 |
0 b |
a . Его фо- |
|||||||||||||
|
a2 |
|
|
b2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
кусы расположены в точках x |
|
c , где c |
|
a2 |
b2 . Решение |
||||||||||||||||||||
задачи об обтекании эллипса сводится к задаче об обтекании круга. Функция, обратная к функции Жуковского w z
z 
 z2 c2 , конформно отображает внешность эллипса на внешность круга z R . Аналитическая в плоскости с разрезом
z2 c2 , конформно отображает внешность эллипса на внешность круга z R . Аналитическая в плоскости с разрезом
c, c ветвь корня выбирается так, что |
z2 |
|
c2 |
0 при дейст- |
|||||||||||||||
вительных z |
c, |
|
. Радиус окружности |
R |
и полуоси эл- |
||||||||||||||
липса связаны |
соотношениями |
a |
1 |
|
R |
1 |
, |
b |
1 |
R |
1 |
, |
|||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
R |
|
|
2 |
|
R |
||
откуда находим R |
a b . В силу формулы (6.55) имеем |
|
|
||||||||||||||||
|
|
1 |
|
|
|
V |
a |
b 2 |
|
|
|
|
|
|
|
|
|
|
|
f z |
V w |
|
|
|
ln w |
|
|
|
|
||||||||||
2 |
|
w |
|
|
|
2 |
i |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
172

1 |
|
|
|
|
|
|
|
|
|
|
|
|
V |
a |
|
|
b 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
z2 |
c2 |
|
|
|
|
|
|
|
z2 |
|
c2 . |
|
|||||||||||||||
V z |
|
|
|
|
|
|
|
ln z |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
z |
2 |
|
c |
2 |
|
|
2 i |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Множитель 1 2 появляется по той причине, что |
|
z2 |
c2 |
z |
( |
|||||||||||||||||||||||||||||
z |
) и потому w ( ) |
|
2 . Избавляясь от иррациональности в |
|||||||||||||||||||||||||||||||
знаменателе, окончательно получаем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 a b 2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z2 |
|
c2 |
|
|
|
|
|
z2 c2 |
|
|
||||||||||||||
|
f z |
|
V z |
|
|
|
|
V z |
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
c2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln z |
|
|
|
z2 |
c2 . |
|
|
|
(6.59) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 i |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
При |
a |
|
c , b |
0 эллипс вырождается в отрезок |
|
c, |
c |
и |
|||||||||||||||||||||||||
из (6.59) находим комплексный потенциал обтекания пластины длины 2c
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
c2 |
|
|
|
|
z2 c2 . |
|||||||
f z |
V V z |
V V |
|
|
|
|
|
|
ln z |
|||||||||||||||||||
2 |
2 |
|
|
|
|
2 i |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Полагая V |
u |
iv |
, где u и v |
|
– действительные функции, |
|||||||||||||||||||||||
находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f |
|
z |
u z |
iv |
|
|
|
z2 c2 |
|
|
|
|
|
ln |
z |
|
z2 |
c2 . |
(6.60) |
|||||||||
|
|
|
|
2 |
|
i |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислим скорость потока. Имеем из (6.60) |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
v |
z |
|
|
|
|
|
|
|
(6.61) |
|||
|
|
|
|
V |
f |
|
z |
|
u |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
i |
z2 |
c2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и при произвольном значении циркуляции |
|
|
скорость потока |
|||||||||||||||||||||||||
обращается в бесконечность на концах пластины, т.е. в угловых точках границы тела. Здесь мы впервые столкнулись со случаем негладкой границы обтекаемого тела. Для таких тел при постановке задачи об обтекании требуются дополнительные физические предположения. Такое условие было найдено С.А. Чаплыгиным.
Пусть обтекаемое тело имеет острие A . Тогда скорость потока должна быть ограничена у острой кромки про-
173

филя. Другая формулировка условия Чаплыгина такова: ост-
рая точка профиля является точкой схода.
Если профиль имеет только одну острую кромку, то условие Чаплыгина однозначно определяет циркуляцию. Поскольку пластина имеет два острия z c , то условию Чаплыгина можно удовлетворить только на одном из них; пусть это условие выполняется при z c . Из условия Чаплыгина и из (6.61) находим единственное возможное значение циркуляции
|
|
|
|
|
|
0 |
2 |
cv |
, |
|
|
|
|
|
|
(6.62) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а для распределения скоростей получаем из (6.61) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
c |
. |
|
|
|
|
(6.63) |
|||
|
|
|
|
|
|
V u |
iv |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
c |
|
|
|
|
|
|
|
||
На острие z |
c скорость потока обращается в бесконечность. |
||||||||||||||||||||||
|
Рассмотрим обтекание профилей Жуковского. Пусть |
– |
|||||||||||||||||||||
дуга, которая проходит через точки z |
a , |
а середина дуги |
|||||||||||||||||||||
есть точка z |
ih , и |
|
|
– окружность с центром в точке |
w |
ih , |
|||||||||||||||||
проходящая |
через |
точки |
w |
a |
(рис. 6.14). Функция |
w |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
z |
|
z2 |
a2 |
конформно отображает внешность дуги |
|
на |
|||||||||||||||||
внешность окружности |
. Заметим, что нормаль к окружно- |
||||||||||||||||||||||
сти |
|
в точке w |
|
|
a образует с действительной осью угол |
||||||||||||||||||
|
arctg h a , а в точке |
w |
a – |
угол |
|
arctg |
h a |
|
. |
||||||||||||||
Пусть C |
– окружность с центром в точке |
w |
ih |
dei |
, кото- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
рая близка к окружности |
и касается с ней в точке w |
a ; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ее |
радиус равен |
R |
|
|
|
a2 |
h2 |
d . |
Функция |
w z |
|
z2 |
a2 |
||||||||||
конформно отображает на внешность окружности |
C |
внеш- |
|||||||||||||||||||||
ность дуги C (рис. 6.14), которая по виду напоминает профиль крыла самолета и называется профилем Жуковского. Решим задачу обтекания профиля Жуковского, сведя ее к задаче обтекания круга. Из (6.55) находим комплексный потенциал
174

|
|
|
|
1 |
|
|
|
|
V R2 |
|
|
|
|
ln w . |
|
|||
|
|
|
f z |
V w |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
w |
2 |
i |
|
||||||
Циркуляцию |
определим из условия Чаплыгина: острая точ- |
|||||||||||||||||
ка профиля должна быть точкой схода. |
Образ точки z a |
|||||||||||||||||
имеет вид Rei |
и из (6.58) находим значение циркуляции |
|||||||||||||||||
|
|
|
2 |
v |
|
|
a2 |
h2 |
|
d sin |
. |
|
||||||
По теореме Жуковского подъемная сила крыла равна |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
v2 |
|
|
a2 |
h2 |
|
|
|
|
|
. |
|
|||
|
|
P |
2 |
|
|
d |
sin |
|
|
|||||||||
w |
y |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ia |
’ |
|
C’ |
|
|
|
|
|
|
|
|
C |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ih |
||
|
ih |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||
-a |
|
|
a |
|
|
x |
|
|
-a |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
- i
–
a
Рис. 6.14
175

ПРИЛОЖЕНИЕ 1 ПОНЯТИЕ ОДНОЛИСТНОСТИ
В главе 2 было введено понятие функции комплексного переменного. Этому понятию можно дать следующую геомет-
рическую интерпретацию. Пусть на множестве |
E расширен- |
|||
ной комплексной плоскости |
z |
определена функция w f z |
и |
|
пусть E – множество |
ее |
значений на |
плоскости |
w |
(рис. П.1.1). Тогда говорят, то задано отображение множест-
ва E |
на множество |
E . Точка w E называется образом |
|
точки z |
E , а точка z |
– прообразом точки w при отображе- |
|
нии w |
f |
z . |
|
z |
|
|
w |
|
|
|
w=f(z) |
|
|
E |
E’ |
Рис. П.1.1
Может оказаться, что некоторые точки множества E имеют не один, а несколько прообразов, т.е. отображение
имеют не один, а несколько прообразов, т.е. отображение
w f z может не быть взаимно однозначным. Если отображение w f z является взаимно однозначным, то функция f z называется однолистной. Приведем более подробное определение однолистности.
176

Определение 1. Функция w f z называется однолист-
ной на множестве E , если она в различных точках множества E принимает различные значения.
Отображение w f z , осуществляемое однолистной
функцией, является взаимно однозначным и называется одно-
листным.
Очевидно, |
функция w f z является однолистной на |
|
множестве |
E , если для любых точек z1 и z2 этого множества |
|
равенство f |
z1 |
f z2 имеет место в том и только в том слу- |
чае, когда z1 |
z2 . Другими словами, |
функция w |
f z |
одно- |
|||||||||||
листна на множестве |
E , |
если это множество не содержит ни |
|||||||||||||
одной пары точек |
z1 и z2 ( z1 |
|
z2 ) таких, что f |
z1 |
f |
z2 . |
|
||||||||
|
Из определения однолистности следует, что если функ- |
||||||||||||||
ция однолистна на множестве |
E и E1 |
E , то эта функция од- |
|||||||||||||
нолистна на множестве E1 . |
|
|
|
|
|
|
|
|
|
||||||
|
Суперпозиция однолистных отображений есть однолист- |
||||||||||||||
ное отображение, т.е. если функция |
f |
z |
однолистна на |
||||||||||||
множестве E ( E |
E1 ), а функция w |
g |
однолистна на E1 |
||||||||||||
( E1 |
E2 ), то функция w |
g |
f |
z |
однолистна на E ( E |
E2 |
|||||||||
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если отображение w |
f |
z |
: E |
E |
является однолист- |
|||||||||
ным, |
то каждой точке w |
E |
|
ставится в соответствие одна и |
|||||||||||
только одна точка |
z |
E |
такая, что |
f z |
w . Тем самым на |
||||||||||
множестве |
E |
определена |
функция |
z |
h w , |
обратная |
к |
||||||||
функции f |
z |
. Справедливы тождества: |
|
|
|
|
|
||||||||
|
f h w |
w , |
w E ; |
|
h f z |
z , z E . |
|
|
|||||||
|
Функция |
w |
f |
z , |
заданная на множестве |
E и отобра- |
|||||||||
жающая E на |
E , |
является однолистной на E тогда и только |
|||||||||||||
177

тогда, когда обратная функция z |
|
h w |
однозначна на множе- |
||||||||||||||||
стве |
E . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Линейная функция |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
w |
f |
z |
|
|
az |
b , |
|
(П.1.1) |
|||||
где |
a и b – комплексные постоянные ( a 0 ), однолистна на |
||||||||||||||||||
всей комплексной плоскости, так как обратная функция |
|
||||||||||||||||||
|
|
|
|
|
|
z |
h w |
|
1 |
w |
|
b |
|
(П.1.2) |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
|
|||
однозначна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция (П.1.1) отображает взаимно однозначно расши- |
||||||||||||||||||
ренную комплексную плоскость |
z на расширенную комплекс- |
||||||||||||||||||
ную плоскость |
w . |
При этом точка |
|
z |
переходит в точку |
||||||||||||||
w |
, а соответствие между конечными точками плоскостей |
||||||||||||||||||
z и w определяется формулами (П.1.1) и (П.1.2). |
|
||||||||||||||||||
|
Рассмотрим случай b |
0 . Тогда |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
w |
az , |
|
|
|
|
(П.1.3) |
|||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
a |
|
z |
|
, |
|
arg w |
|
arg a |
arg z . |
(П.1.4) |
|||||
|
|
|
|
|
|
|
|||||||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
w=az=|a|ei z |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|a|r |
|
Рис. П.1.2
Из равенств (П.1.4) следует, что отображение (П.1.3) сводится к подобному растяжению плоскости z в a раз с центром по-
добия в начале координат и повороту всей плоскости вокруг
178

точки z |
0 |
|
на угол |
arg a . |
При отображении (П.1.3) |
луч |
|||||||||||||||||||||||
arg z |
|
переходит в луч |
arg w |
|
, а окружность |
|
z |
|
r – |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
в окружность |
w |
|
|
a |
r (рис. П.1.2). Круг |
z |
|
|
r |
при этом ото- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
бражении переходит в круг |
w |
|
a |
r . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Если |
|
a |
|
1 , |
т.е. a |
ei |
, |
то преобразование (П.1.3) есть |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
поворот плоскости на угол |
|
. В частности, преобразование |
|||||||||||||||||||||||||||
w |
iz есть поворот на угол |
|
2 , а преобразование w |
|
z есть |
||||||||||||||||||||||||
поворот на угол . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Преобразование (П.1.1) есть суперпозиция преобразова- |
||||||||||||||||||||||||||||
ний |
|
|
a |
|
z , |
|
|
ei arg a , |
w |
|
b . Поэтому преобразование |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
w |
az |
b можно осуществить, выполнив в указанном порядке |
|||||||||||||||||||||||||||
следующие преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
а) подобное растяжение плоскости |
z |
в |
|
a |
|
раз (центр по- |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
добия в точке z |
|
|
0 ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
б) |
поворот |
плоскости |
|
|
вокруг |
точки |
0 |
на |
угол |
|||||||||||||||||||
|
arg a ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
в) параллельный перенос плоскости |
|
на вектор b . |
|
|||||||||||||||||||||||||
|
Пример 2. Функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
1 z |
|
|
|
|
|
|
|
|
(П.1.5) |
|||||
отображает взаимно однозначно расширенную комплексную
плоскость z |
|
на расширенную комплексную плоскость |
w (об- |
|||||||||||||||||
ратная функция z |
1 w однозначна). При этом точке z |
0 со- |
||||||||||||||||||
ответствует точке |
w |
, |
а точке |
z |
|
– точка |
|
w |
0 . |
Луч |
||||||||||
arg z |
|
переходит при отображении (П.1.5) в луч |
|
arg w |
, |
|||||||||||||||
окружность |
|
z |
|
r |
– в окружность |
|
w |
|
1 r , круг |
|
z |
|
R |
– на |
||||||
|
|
|
|
|
|
|||||||||||||||
область |
|
w |
|
1 R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 3. Рассмотрим функцию |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
w z2 . |
|
|
|
|
|
|
|
(П.1.6) |
||
Если z2 |
|
z2 |
, то либо z |
z |
2 |
, либо |
|
|
|
|
|
|
|
|
|
|||||
1 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
179
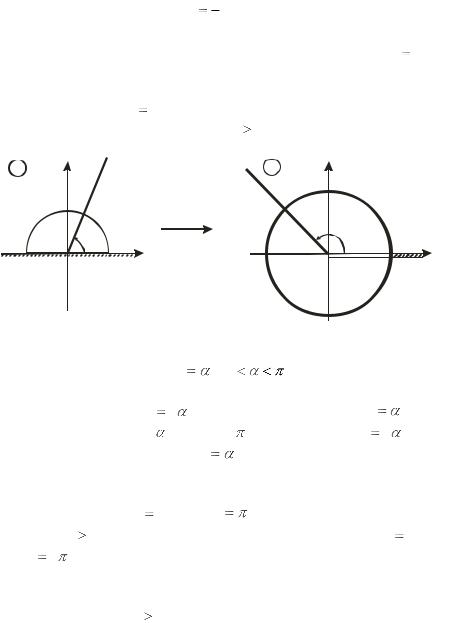
z1 z2 . (П.1.7)
Две точки, связанные равенством (П.1.7), симметричны отно-
сительно начала координат. Следовательно, функция w z2 , однолистна в области D в том и только в том случае, когда эта область не содержит ни одной пары точек, симметричных относительно точки z 0 . В частности, функция (П.1.6) однолистна в верхней полуплоскости Im z 0 .
z |
|
|
|
|
|
|
|
|
|
= |
|
|
z |
|
|
|
arg |
|
|
|
|
|
|
|
0 |
|
|
w=z2
w
arg w =2
2
0






 2e2 i
2e2 i
Рис. П.1.3 |
|
|
Рассмотрим луч arg z |
( 0 |
), лежащий в верхней |
полуплоскости (рис. П.1.3). При отображении (П.1.6) этот луч
переходит в луч |
arg w |
2 |
. Будем вращать луч |
arg z |
, не- |
|||
прерывно увеличивая |
|
от 0 до |
. Тогда луч |
arg w 2 |
, яв- |
|||
ляющийся образом луча |
arg z |
, будет поворачиваться про- |
||||||
тив часовой стрелки. Если луч на плоскости z |
опишет верх- |
|||||||
нюю полуплоскость, |
то его образ опишет всю плоскость w . |
|||||||
При этом лучи |
arg z |
0 |
и |
arg z |
, образующие границу об- |
|||
ласти |
Im z 0 , |
перейдут |
соответственно в лучи arg w |
0 и |
||||
arg w |
2 . Геометрически эти лучи совпадают с положитель- |
|||||||
ной действительной полуосью на плоскости w . Для того чтобы отображение (П.1.6) было взаимно однозначным не только внутри области Im z 0 , но и на ее границе, проведем в плоскости w разрез по положительной части действительной оси и
180
