3750

Определим АНВТ как

Q 1

Im g

0, 0 .

(6.35)

Из формулы (6.32) получим

g

0, 0

Lq

0

1

0 q

0

,

(6.36)

где

L – длина

дислокации.

В

длинноволновом

пределе (

q

1 d ), учитывая быструю сходимость ряда в выражении

(6.33), можно полагать, что

Kd

2

m l

~ 1 и

1

0

l

q

0

2

g

2

m

.

(6.37)

A

l

2

m 1

Q 1

Im

1

.

(6.38)

1

1

g

0

l

2

g

2 m

2 A

l

m 1

В случае жесткого закрепления дислокации на точечных

дефектах d 0

1

0

и для АНВТ имеем

A

Q

1 Im

1

.

(6.39)

1

1

g

0

2

g

2 m

m 1

l

g s q q2C 2M i B

1 .

(6.40)

2

2

M

B

C

b .

(6.41)

2

y2

t

t

2

ции; C

– сила на единицу длины,

обусловленная натяже-

y2

нием изогнутой дислокации; b – сила на единицу длины за

счет внешнего сдвигового напряжения

.. Динамические ха-

b2 ;

2

b2

M

C

,

(6.42)

1

суммирование, получим точную формулу для

Q 1

с учетом

всех гармоник. Если представить в выражении (6.39)

1

a

a

a

2

,

(6.43)

2

0

1

2

g s

2 m l

m 1

где a0 ,

a1 ,

a2 определить как коэффициенты разложения в

ряд по

, то получим

Q 1

5

Im

1

5

B

.

6

102 C

2M i B

6 10 C

2M

2

2B2

l

l

2

Рассмотрим возможность разложения функции

в

ряд. Для этого запишем

1

1

2 g s

2 m l

g s

2 m l g 0

m 1

m

1

2 m l 2

1

2M i B

1

C

2M i B

1

C

1

1

1

l

2

1

1

2 m l 2

z2

Cz2

C m

2

m

m2

lz

2

z2

2

Cz2tg

lz

C

C

2

,

l

2

2

2

lz

1

l

ctg

lz

1

tg

lz

lz

ctg

2z

2

z2

2

2

2

lz

2

z

2

где

z2

2M

i

B C .

Из

полученного

выше выражения

видно,

что

функция

становится неопределенной

при

tg

lz

lz

, а,

следовательно, при

lz

9

. Отсюда при

B

0

по-

2

2

2

2

лучаем

3

C

3

1 , где

1 – частота первой гармоники в

l

M

ния возможность разложения функции

в ряд по

обес-

печивается ее аналитичностью в круге

3 1 . С увеличением

коэффициента динамического торможения дислокации

B ра-

g 1

b2

q2

q4c4

4

k 2

2

c2

q

1

t

ln

0

t

8

ct2

2

q2

2

ct2

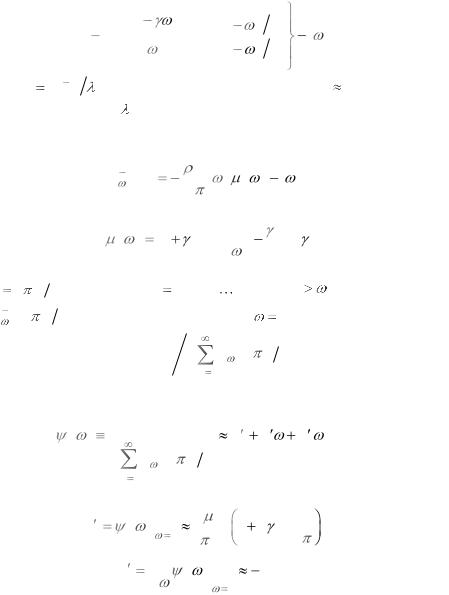
q

2

2

2

2

ct

2

2

2

ln

k0

cl

i

B ,

(6.44)

c2 2

q2

2

c2

t

l

где k

0

2e C

– предельное волновое число,

C

0, 577 – по-

b2

q 1 0

2

i B ,

(6.45)

4

где

2 ln

ct k0

2

1

ln .

(6.46)

2

q

2

m l .

Так

как m

1, 2, 3,

,

то ct q

и функции

g 1

2

m l

аналитические в точке

0 и ее окрестности.

Следовательно,

функция

1 2

g

2 m l

также аналитиче-

m 1

1

a

a

a

2 .

(6.47)

0

1

2

2 g

2

m l

m 1

Определим коэффициенты разложения:

a

3 b2

1 2 ln

k0l

;

0

0

l2

2

a

d

1

iB ;

1

d

5

0

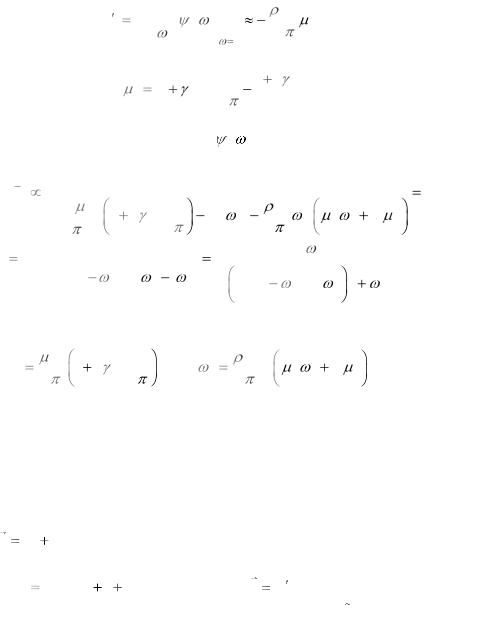
a2

1 d 2

b2

0 ,

2 d

2

20

0

где введено обозначение

0

1 2

ln

k0l

1 3 2

.

(6.48)

2

4

затем

полученную функцию

и выражение (6.45) в

формулу (6.39), для внутреннего трения будем иметь

Q 1

Im

1

3

b2

k l

6

b2

1

1 2 ln

0

i

B

2

0

l2

2

5

4

5

5

Im

1

5

B

.

6

102 D

2M

i B

6 10 D 2M

2

2 B2

l

l

2

(6.49)

Здесь

D

b2

1

2

ln

k0l

,

M

b2 5

1

0

(6.50)

4

2

4

6

5

ническим

и

характеризуется комплексным

потенциалом

f z u

x, y

iv x, y , так что V f z .

Пусть на плос-

стью V

, а само тело покоится. Тогда комплексный потенциал

потока – аналитическая в D функция, причем f

V . Раз-

ложение ее в ряд Лорана в окрестности точки z

:

c 1

c

2

.

(6.51)

f

z

V

z

z2

Находим 2

ic 1

iN ,

где

и

N

– циркуляция и поток

вдоль простой замкнутой кривой, охватывающей тело D . В

области D , по условию,

нет источников, так что

N 0 , и из

(6.51) получаем

c 2

(6.52)

f

z

V

z

c

ln z

2 i

z

в окрестности точки z

. Скорость V

и значение циркуля-

ции

должны быть заданы – это и есть граничное условие на

бесконечности для комплексного потенциала f z

. Граничное

условие на поверхности тела S таково: скорость потока долж-

на быть направлена по касательной к S

в любой точке конту-

ра. Следовательно, граница

S – одна из линий тока, так что на

S выполняется краевое условие

const .

(6.53)

v

x, y

s

Итак,

требуется найти функцию f

z ,

которая аналитична в

области D , имеет разложение (6.52) в окрестности точки z

, где V

и

– заданные комплексная и действительная посто-

янные, и удовлетворяет краевому условию (6.53) на контуре S

.

.

Теорема 1. Решение задачи обтекания единственно.

Доказательство. Пусть имеются два комплексных по-

тенциала f1

z

и

f2 z

– решения задачи обтекания тела. То-

гда их разность

f

z

f1

z

f2 z

аналитична и ограничена

в области D , принимает постоянные значение на

S , и по тео-

реме единственности решения задачи Дирихле

v x

const .

Следовательно, f z const , потенциалы f1 z и

f2 z

отли-

Обтекание тела называется бесциркулярным, если

0 и

циркулярным, если

0 .

Теорема 2. Потенциал

w

f z

бесциркулярного обте-

кания тела конформно отображает область D на внешность

отрезка, параллельного действительной оси.

Доказательство. Без ограничения общности можно счи-

тать,

что v

s

0 . Покажем, что существует функция w

g z ,

которая конформно отображает область D на внешность от-

резка

действительной

оси

и

имеет

разложение

g z

V z

g0

в окрестности точки z

. Тогда

g z

тенциалом: по теореме 1

f z

g

z

const .

Пусть функция w

h z

конформно отображает область

D на внешность отрезка

0, 1 . Тогда она имеет простой по-

люс в точке z

и в ее окрестности разлагается в ряд

h z

h 1z

h0

h1

.

z

Функция w

h z 1

1

конформно отображает область D на

некоторую область

D1

как суперпозиция однолистных функ-

ций.

При

малых

z

имеем

w

z

h 1

h0 z

, так что

w 0

0 ,

w

0 h 11 . По теореме Римана для любого действи-

тельного

существует функция

h

z ,

которая конформно

отображает

D

на

D1 ,

такая, что

arg h

0

. Положим

argV и затем g z

V

1

. Это и есть искомая