3750

периодом

2 и имеют только действительные нули z k и

z

k

соответственно, где

k Z ;

2

г)

sin z – нечетная функция,

cos z – четная функция;

sin2 z cos2 z 1 ,

cos2 z

sin2 z

cos 2z

sin 2z

2sin z cos z ,

sin

z1

z2

sin z1 cos z2

cos z1 sin z2 ,

cos

z1

z2

cos z1 cos z2

sin z1 sin z2 ;

(2.2)

е) имеют место формулы

sin(x

iy)

sin x ch y

i cos x sh y ,

cos(x iy)

cos x ch y

i sin x sh y .

(2.3)

Функции

tg z

и

ctg z

определяются

равенствами:

tg z

sin z

и ctg z

cos z

.

cos z

sin z

4. Гиперболические функции определяются равенствами:

ez

e z

ez

e

z

sh z

ch z

sh z

, ch z

,

th z

,

cth z

.

2

2

ch z

sh z

Тригонометрические и гиперболические функции связа-

ны между собой следующими соотношениями:

sin z

i sh iz ,

sh z

i sin iz ,

cos z ch iz ,

ch z

cos iz ,

tg z

i th iz ,

th z

i tg iz ,

ctg z

i cth iz ,

cth z

i ctg iz .

(2.4)

Таким образом,

свойства функций sh z

и

ch z

непосредствен-

но вытекают из свойств функций

sin z

и cos z . Отметим, в ча-

стности, что функции

sh z

и

ch z непрерывны на всей ком-

плексной плоскости. Имеют место формулы

ch2 z

sh2 z

1 ,

ch2 z

sh2 z

ch 2z ,

2sh z ch z

sh 2z ,

sh z1

z2

sh z1 ch z2

ch z1 sh z2 ,

ch

z1

z2

ch z1 ch z2

sh z1 sh z2 .

(2.5)

5. Логарифмическая функция

Ln z

( z

0 )

определяется

как функция, обратная показательной ez , причем

,

k Z .

Ln z ln

z

i Arg z

ln

z

i arg z

2k

зывается

то, которое получается при

k

0 ;

оно равно

i arg z . Очевидно, что Ln z

i . Для лога-

ln z ln

z

ln z

2k

Ln z z

2

Ln z

Ln z

2

,

Ln

z1

Ln z Ln z

2

.

1

1

z2

1

6. Обратные тригонометрические

функции

Arcsin z ,

пример, если

z

sin w , то w называется арксинусом числа z и

обозначается

w

Arcsin z . Все эти функции являются много-

Arcsin z

i Ln iz

1

z2

,

Arccos z

i Ln z

z2

1 ,

Arctg z

i

Ln

1

iz

,

Arcctg z

i

Ln

z

i

.

(2.6)

z

i

2

1

iz

2

Главные значения обратных тригонометрических функ-

ций arcsin z ,

arccos z ,

arctg z ,

arcctg z получаются,

если брать

ся w

Arsh z . Все эти функции являются многозначными и

выражаются через логарифмические функции:

Arsh z

Ln

z

z2

1

, Arch z

Ln

z

z2 1 ,

Arth z

1

Ln

1

z

,

Arcth z

1

Ln

z

1

.

(2.7)

2

1

z

2

z

1

Главные значения обратных гиперболических функций

arsh z ,

arch z ,

arth z ,

arcth z

получаются, если брать главные

значения соответствующих логарифмических функций.

8.

Общая степенная функция w

za , где a

i –

любое комплексное число, определяется равенством za

ea Ln z

. Эта функция многозначная, ее главное значение равно

ea ln z .

Если a

1

( n N ), то получаем многозначную функцию – ко-

n

рень n -й степени из комплексного числа:

1

i

arg z 2k

ln

z

i arg z 2k

z1 n n z en

n

z

e

n .

9. Общая показательная функция w

az

( a

0 – любое

комплексное число) определяется равенством

az

ez Ln a .

Главное значение этой многозначной функции равно ez ln a .

Пример 7. Вычислить w

sin z при z0

i ln(2

5) .

Решение. Согласно формулам (2.3) получаем

w0

sin z0 sin

ch ln(2

5)

i cos

sh ln(2

5)

1

i sh ln(2

i

(eln(2

5)

e

ln(2

5) )

5)

2

i

1

i 8 4 5

i

4 2

5

2i .

2 5

2

2 2

2

5

5

2

5

функции

ii

ei Ln i

ei ln

i

i arg i

2k

e

2

2k

e

1 2

2k .

Пример 9. Записать в алгебраической форме

Arctg(1

i) .

Решение. Согласно формуле

Arctg z

i

Ln

1

iz

полу-

2

1

iz

чаем

Arctg 1

i

i

Ln

1

i

1

i

i

Ln

i

i

Ln

1

2i

.

2

1

i

1

i

2

2

i

2

5

По

формуле

ln

z

i arg z

2k

i

( k

Z )

Ln z

ln

z

iArg z

имеем

Ln

1

2

i

1

ln 5

i

arctg2

2k

i .

Оконча-

5

5

2

тельно получаем

Arctg 1

i

1

arctg2

2k

1

i

ln 5 .

2

2

4

Пример 10. Решить уравнение sin z

3 .

Решение. Задача сводится к нахождению величины

z

Arc sin 3 .

По формуле (2.6) получаем

z

Arcsin 3

i Ln(3i

8)

i Ln i

i

i arg 3

2k

i

3 8

ln 3

8

8

2k

i ln

, где

k

Z .

3

8

2

Пусть дана последовательность

zn

комплексных чисел:

z1, z2 ,

, zn ,

Определение 1. Комплексное число

a

называется преде-

лом последовательности

zn

, если для любого положитель-

ного числа

можно указать такой номер N

N

, начиная с

которого все элементы zn

этой последовательности удовлетво-

ряют

неравенству

zn

a

при n

N

.

Последователь-

ность zn

, имеющая предел

a , называется сходящейся к чис-

лу a , что записывается в виде

lim zn

a .

n

Каждой последовательности комплексных чисел

zn

со-

ответствуют две

последовательности

действительных

чисел

xn

и yn

, где zn

xn

iyn ,

n 1, 2,

Теорема 1. Последовательность

zn

xn

iyn

сходится

к числу a

i

тогда и только тогда, когда lim xn

и

n

lim yn

.

n

Определение 2. Последовательность

zn

называется ог-

раниченной, если существует положительное число

M такое,

что для всех элементов

zn

этой последовательности выполня-

ется неравенство

zn

M .

Теорема 2. Всякая сходящаяся последовательность ог-

раничена.

Если lim zn

a и

lim

n b , то

n

n

1. lim (zn

n ) a

b ;

n

2. lim (zn

n ) ab ;

n

3.

lim

zn

a

(

n

0 ,

b

0 ).

b

n

n

Достаточное условие сходимости последовательно-

сти

комплексных

чисел.

Пусть

z

n

r ei

n ,

где

r

z

n

,

n

n

n

arg zn .

Тогда,

если

lim rn

r0

и

lim

n

0 ,

то

n

n

lim z

n

r ei

0 .

n

0

Если для сколь угодно большого числа

M

0 существу-

ет натуральное число N

такое,

что все члены zn последова-

тельности с

номерами

n

N

удовлетворяют

неравенству

zn

M , то говорят,

что последовательность

zn

сходится к

пишут lim zn

.

n

Дополняя плоскость комплексного переменного так вве-

денной бесконечно удаленной точкой z

, получаем расши-

ренную плоскость комплексного переменного.

Окрестностью бесконечно удаленной точки называется

совокупность

всех точек z , удовлетворяющих неравенству

жащая эту

точку;

-окрестностью

точки

z0

называется

множество всех точек

z , лежащих внутри круга радиуса

с

центром в точке z0 ,

т.е. множество всех точек

z , удовлетво-

ряющих неравенству

z

z0

.

Пусть функция

f

z определена в некоторой окрестно-

сти

точки z0 , кроме, быть может, самой точки z0 .

Определение 4.

Число

A называется пределом функции

f z

в точке z0 , если для любого числа

0 можно указать

такое число

0 , что для всех точек z

, удовлетво-

ряющих условию

0

z z0

,

выполняется

неравенство

f z

A

. В этом случае пишут

lim f

z

A . Здесь пред-

z

z0

вательность значений функции

f

zn

сходится к одному и

тому же комплексному числу A ,

то число A называют преде-

лом функции f z

в точке

z0 :

lim

f

z

A . Здесь конеч-

z

z0

ность z0 и A не предполагается.

Существование предела lim

f

z

, где

z

z0

f z

u x, y iv x, y ,

z0

x0

iy0 ,

равносильно существованию двух пределов

lim u x, y и

x

x0

y

y0

lim v x, y , причем

lim f

z

lim u x, y

i lim v x, y .

x x0

z z

0

x x0

x x0

y y0

y

y0

y y0

Пределы функций комплексного переменного обладают

следующими свойствами. Пусть существуют пределы

lim f

z

A и

lim g z

B .

z z0

z

z0

lim

f

z

g z

A

B ,

z

z0

lim

f

z g

z

AB ,

z

z0

lim

f

z

A

,

B

0 .

g

z

B

z

z0

Определение 6.

Функция f

z

, заданная в области

D ,

называется непрерывной в точке z0

D , если

lim

f

z

f

z0 .

z

z0

Иными словами: функция f z

непрерывна в точке

z0

D ,

если

для

любого

числа

0

можно

указать

такое

число

0 , что для всех точек

z

D , удовлетворяющих ус-

ловию

z

z0

, выполняется неравенство

f z

f z0

.

Для непрерывности функции комплексного переменного

f z

u

x, y

iv x, y

в точке z0

x0

iy0 необходимо и дос-

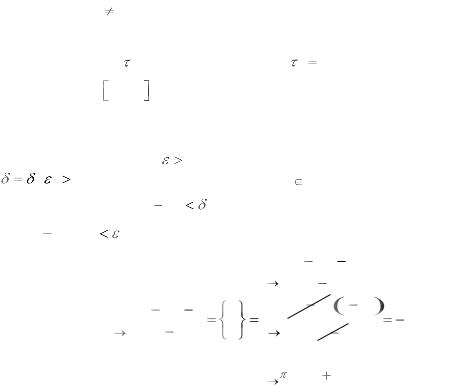
Определение 7. Функция

f

z

комплексного переменно-

го называется непрерывной в области D , если она непрерывна

в каждой точке этой области.

Определение 8. Сумма, разность и произведение двух

функций комплексного переменного

f

z

и g

z

, непрерыв-

ных в области D , также являются непрерывными функциями в

этой области, а функция

f

z

непрерывна в тех точках облас-

g

z

ти D , где g z

0 .

Определение 9. Если функция

f

z

непрерывна в точке

z0 , а функция F

непрерывна в точке

0

f

z0 , то слож-

ная функция F

f

z

непрерывна в точке z0 .

Определение 10. Функция

f z

комплексного перемен-

ного называется равномерно непрерывной в области

D , если

для

любого

числа

0

можно

указать

такое

число

0 , что для любых точек

z1, z2

D ,

удовлетворяю-

щих

условию

z1

z2

,

выполняется

неравенство

f z1

f z2

.

Пример 11. Вычислить предел

lim

z2

4iz 3

.

z

i

z

i

Решение.

lim

z

2

4iz

3

0

lim

z

i

z

3i

2i .

z i

0