3750

(5.8). Разложим функцию

f

z

1

в ряд в окрестности

1

z4

бесконечно удаленной точки:

f

z

1

1

1

1

1

1

4

4

1

4

8

12

1

z

z

1

z

z

z

z4

Из этого разложения видно, что res f

c

1

0 . Таким об-

разом согласно формуле (5.8) получим

dz

4

2 i

res f zk

2

i res f

0 .

2 1 z4

z

k 1

y

y

z2

z

z1

z3

1

x

z4

_

3 x

1

2

2

2

z3

z4

z2

z5

Рис. 5.7

Рис. 5.8

Пример 19. Вычислить интеграл

z17dz

.

z

3

z2

2 3

z3

8 4

Решение. Корни знаменателя подынтегральной функции

z1 i 2 , z2

i

2 ,

z3

1

i

3 ,

z4

2 , z5

1

i 3 являются

полюсами,

так

как

функцию

можно

записать

в

виде

z17

z17

.

z2 2 3 z3 8 4

z z

3 z z

2

3 z z

4 z z

4

4

z z5 4

1

3

Замечаем, что все полюса

z1, z2 ,

z3, z4 , z5

лежат внутри кон-

тура интегрирования на окружностях

z

и

z

2 (рис.

2

5.8). Поэтому по теореме Коши о вычетах имеем

z17dz

5

zk .

I

2

i

res f

2 3 z3 8 4

z

3 z2

k 1

f z

z17

1

1

1

2

3

8

4

z

2

3

8

4

z6 1

z12

1

1

1

z2

z3

z2

z

3

1

1

6

24

1

32

640

1

6

32

z

z2

z4

z3

z6

z

z3

z4

Из этого разложения видно, что

res f

c 1 1 . Таким

образом согласно формуле (*) получим

I

z17dz

2

i .

z

3 z2 2 3 z3

8 4

интеграл I

R

x dx ,

где

R x

–

рациональная функция,

R x

Pm

x

, где

Pm x

и Qn x

– многочлены степеней m и

Qn

x

n , соответственно. Если R x

непрерывна на всей действи-

тельной оси ( Qn x

0 ) и n

m

2 , то

I

R x

dx

2 i

res R

z ,

(5.9)

z

zk

Im zk 0

где вычеты берутся по всем полюсам функции R

z , располо-

женным в верхней полуплоскости.

dx

Пример 20. Вычислить интеграл

I

.

x2

1 4

Решение. Здесь m 0 ,

n

8 , поэтому данный интеграл

сходится. Введем функцию f

z

1

, которая на дейст-

z2 1 4

Функция f z , имеет в верхней

полуплоскости

( Im z

0 )

единственную особую точку – полюс четвертого порядка z0

i

. Поэтому, согласно формуле (5.9), I

2 i Res f z

, i . Нахо-

дим вычет функции относительно полюса

Res

f z

, i

1

lim

z i

4

20 lim

1

5

i

z i 4 z i 4

3! z i

z i z i 7

32

и получаем I

dx

2

i

5

i

5

.

x2

1 4

32

16

2. Интегралы вида

R

x cos

x dx и

R

x sin

x dx ,

где

R x

–

правильная рациональная дробь,

0 –

любое

действительное число. Так как

R

x cos

x dx

Re

R

x ei xdx ,

R

x sin

x dx

Im

R

x ei xdx ,

z

. Тогда при

0 lim g z ei z dz 0 , где CR – по-

R

CR

функции R z

, то по формуле (5.9) имеем

ei

x R x dx

2

i

res

ei

z R

z .

(5.10)

z zk

Im zk

0

Замечание. Если

0 , то

ei

x R x dx

2

i

res

ei

z R

z ,

(5.11)

Пример 21. Вычислить интегралы

x 1 cos 5x dx

и

x2 2x 5

x

1 cos 5x dx

x

1 e5ix

Re

dx ,

x2

2x

5

x2

2x

5

x

1 sin 5x dx

x

1 e5ix

Im

dx .

x2

2x

5

x2

2x

5

z

1 e5iz

Рассмотрим функцию

, значения которой совпадают

z2

2z 5

x

1 e5ix

ции

. Функция

x2

2x

5

f

z

z

1

z 1

z2

2z 5

z 1 2i z 1 2i

полюс первого порядка z0

1 2i и lim f

z

0 . Поэтому, со-

z

гласно формуле (5.10),

x

1 e5ix

z

1 e5iz

dx 2

iRes

, 1

2i

x2

2x

5

z2

2z

5

2 i

z

1 e5iz

ie

10 cos 5

i sin 5 .

z2

2z 5

z

1 2i

I

sin ax

dx

( a 0 , b 0 ).

(1*)

0 x x2 b2

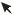Cr

0

x

Рис. 5.9

Решение. Введем функцию

f

z

eiaz

такую, что

z z2 b2

при z x ее мнимая часть Im f

z

совпадает с подынтеграль-

ной функцией в (1*). Функция f

z

имеет особенность на ве-

щественной оси – полюс первого порядка в точке

z 0 . По-

лишь один полюс функции f z

в точке z ib . Согласно тео-

реме Коши о вычетах

r

eiax

eiaz

R

eiax

R

dx

dz

r

dx

x x2 b2

C z z2

b2

x x2 b2

r

eiaz

dz

2

i

,

(2*)

C

z

z2

b2

R

где

Res

eiaz

, ib

lim

eiaz

z

ib

e

ab

.

(3*)

z z2

b2

2

b2

2b2

z ib z z

Заменяя в первом интеграле (2*)

x на

x

и объединяя его с

третьим интегралом, получим

r

eiax

R

eiax

dx

dx

R x x2

b2

r x x2

b2

R eiax

e iax

R

sin ax

dx .

(4*)

dx

2i r

r x

x2

b2

x

x2

b2

Так как lim

eiaz

1

, то подынтегральная функция пред-

b2

b2

z

0 z2

ставима в виде

eiaz

1 1

z

,

где

lim

z

0 .

z z2

b2

b2

z

z

z 0

Полагая z

rei

, находим

eiaz dz

1

dz

z

dz

i

0

i

rei

d

. (5*)

C z z2

b2

b2 C

z

C

z

b2

r

r

r

Интеграл в правой части (5*) при r

0 имеет пределом нуль

0

lim

rei

d

0 .

(6*)

r

0

вой части (2*) стремится к нулю при R

, так как функция

g z

1

стремится к нулю при z

:

z

z2

b2

lim

eiaz

dz

0 .

(7*)

2

2

R

C

z

z

b

R

Таким образом, при

R

и r

0

равенство (2*) с учетом

соотношений (3*)–(7*) принимает вид

2i 0

sin ax

dx

i

i

e

ab

,

x x2

b2

b2

b2

откуда

sin ax

dx

1

e ab .

0 x

x2

b2

2b2

3. Интегралы вида

2

I

R

cos x, sin x

dx ,

(5.12)

0

где R – рациональная функция аргументов

cos x и sin x , огра-

ниченная внутри промежутка интегрирования.

Полагаем eix

z , тогда

dx

dz

,

cos x

z2

1

,

sin x

z2

1

.

iz

2z

2iz

Очевидно, что в этом случае

z

1 ,

0

x

2 и интеграл

(5.12) принимает вид

I