
m0936
.pdf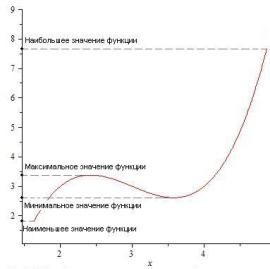
3. Выбираем наибольшее и наименьшее значения функции сравнением значений функции в критических точках и на концах интервала.
Рис. 9.15. Наибольшее и наименьшее значения функции на отрезке
9.4.5.Асимптотические свойства функций
Вприложениях математики область существования функции представляет собой, как правило, объединение отдельных интервалов непрерывности, разделенных точками разрыва первого и второго рода (см. раздел 7.4).
Внекоторых точках разрыва второго рода график функции с одной стороны или с двух сторон может неограниченно приближаться к вертикальной прямой, проходящей через точку разрыва. Эта линия называется вертикальной асимптотой графика функции, а поведение функции в окрестности этой точки будем называть асимптотическим. Особенности этого поведения (асимптотические свойства) исследуются с помощью односторонних пределов (см. раздел 7.4, пример 2).
Кроме точек разрыва функция может иметь «линии разрыва», которые являются наклонными или, в частном случае, горизонтальными асимптотами.
131
Примеры наклонных, горизонтальных и вертикальных асимптот уже рассматривались в подразделе 4.5.3, посвященном гиперболе (см. часть I практикума). Про-
должим изучение различных асимптот и особенностей поведения функций в окрестности этих линий.
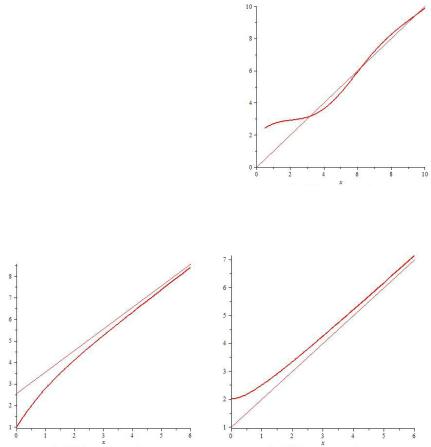
Прямая линия называется асимптотой кривой (в частности, графика функции), если по мере удаления от начала координат расстояние от точки линии до асимптоты стремится к нулю (рис. 9.16– 9.18).
Замечание. График функции может не иметь ни одной асимптоты.
Рис. 9.17. Пример асимптоты 2 |
Рис. 9.18. Пример асимптоты 3 |
Для удобства исследования функции принято различать вертикальные и наклонные асимптоты; горизонтальные асимптоты, как правило, относят к наклонным.
Если график функции неограниченно приближается к вертикальной прямой, то, очевидно, функция имеет разрыв второго рода. Поэтому вертикальные асимптоты могут быть только в точках разрыва второго рода. Алгоритм нахождения вертикальных асимптот состоит в следующем:
– находятся точки разрыва функции;
132
–в точках разрыва вычисляются односторонние пределы;
–если в некоторой точке разрыва х0 хотя бы один из односторонних пределов равен или , то график функции имеет вертикальную асимптоту с уравнением х = х0.
Замечание. Для правильного построения графика функции необходимо считать оба односторонних предела во всех точках разрыва.
Пример 1. Найти вертикальные асимптоты графика функ-
|
1 |
|
1 |
|
2 |
|
|
||
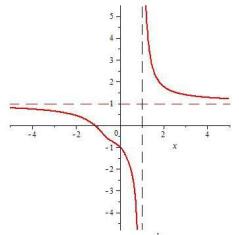
ции y e x |
|
|
(рис. 9.19). |
|
|
||||
x 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y e |
2 |
|
|
|||||
|
|
|
|
|
Рис. 9.19. График функции |
|
x |
|
|
|
|||||||||||
|
|
|
|
|
|
x 1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Точками разрыва функции являются x1 0 |
и x2 1. |
|||||||||||||||||||
|
1. Вычисляем |
левый |
предел |
|
в |
|
точке |
x1 0: |
|||||||||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
e |
|
x2 |
|
0 1 1. Предел не бесконечен, поэтому вы- |
||||||||||||||||
|
x 1 |
||||||||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
числяем правый предел: lim e |
|
x2 |
|
|
|
0 1 1. Предел не |
|||||||||||||||
|
x 1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечен, значит, вертикальной асимптоты в точке x1 0 нет.
133
2. Вычисляем |
|
|
левый |
предел |
в |
точке |
x2 1: |
|||||||
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
lim |
e |
|
x2 |
|
|
|
. |
Предел бесконечен, значит, гра- |
||||||
|
x 1 |
|
||||||||||||
x 1 0 |
|
|
|
|
|
e |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фик функции имеет асимптоту x 1.
Наклонные асимптоты предполагают неограниченное возрастание модуля аргумента x (x или x ). Алгоритм нахождения наклонной асимптоты функции y f x при x (пра-
вой асимптоты) состоит в следующем:
– вычисляется предел lim f x ; если этот предел не сущест-
x x
вует или бесконечен, то график функции не имеет правой асим-
птоты. Если lim f x k R, то переходим к следующему пункту
x x
алгоритма;
– вычисляется предел lim f x kx ; если этот предел не су-
x
ществует или бесконечен, то график функции не имеет правой
асимптоты. Если lim f x kx b R, то правая асимптота су-
x
ществует |
и |
ее |
уравне- |
ниеy kx b. |
|
|
|
Алгоритм нахождения левой асимптоты выглядит аналогично, только все пределы надо вычислять при x .
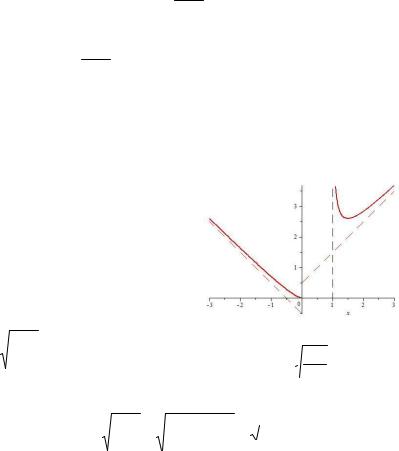
Пример 2. Найти наклонные асимптоты графика функции
y |
x3 |
|
|
(рис. 9.20). |
|
|
||
|
x 1 |
|
Решение.
1. Ищем правую асимптоту:
Рис. 9.20. График функции
y
x3
 x 1
x 1
|
y |
|
1 |
|
x3 |
|
|
|
x3 |
|
|
|
а) lim |
lim |
|
lim |
|
|
1 1, k 1; |
||||||
|
|
|
x 1 |
|
x2 |
|||||||
x x |
x x |
|
x x3 |
|
|
|
||||||
134

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
y 1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
б) |
lim y kx lim |
|
|
|
|
x lim |
|
|
|
|
|
|
|
|
|
|
|
y 1 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
x |
x 1 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
1 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
y 3y 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
lim |
|
1 |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
, |
|||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y |
y2 3y 3 |
|
y 1 |
2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b |
1 |
|
. Правая асимптота есть, ее уравнение |
|
|
y x |
1 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2. Ищем левую асимптоту: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
y |
|
|
1 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1; |
||||||||||
|
а) |
lim |
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
1 1, |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
x x |
|
x x |
|
|
|
|
|
|
|
x x3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
z3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
б) |
lim y kx lim |
|
|
|
|
|
|
|
|
x |
lim |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
z |
|
|
|
z 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y 1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
y 1 |
... |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
1 |
. Левая асимптота есть, ее уравнение y x |
1 |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи к разделу 9.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
9.4.1. Найти точки экстремумов функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
а) y 5x 6 x2; б) y x4 13x2 36; в) y |
1 |
|
|
|
|
|
; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
г) |
y e |
2 ; д)y x2e x ; е) y ln 6x 8 x2 ; ж) |
y sinx; |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
з) |
y x cosx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
9.4.2. Найти точки экстремумов функций и промежутки возрастания и убывания:
а) y 5
 2 x 2 ; б) y 3
2 x 2 ; б) y 3
 x 3 2 3
x 3 2 3 x 5 2 ; в) y x3
x 5 2 ; в) y x3 x 1.
x 1.
9.4.3. Найти точки экстремумов функций:
а) y x2 6x 8 ; б) y x2 6x 8; в) y x2 6x 8 ;
г) y sinx ; д) y arcsin sinx .
135

9.4.4. Найти наибольшее и наименьшее значения функций в их областях существования:
а) y cosx; б) y arccosx; в) y 
 7x x2 10;
7x x2 10;
г) y ln 7x x2 10 .
9.4.5. Найти наибольшее и наименьшее значения функций на заданных интервалах:
а) |
y x2 |
8x 12 на интервале 3, |
7 ; |
|
|||||||||||||||||||||
б) |
y |
|
1 |
|
|
|
|
|
на интервале 1,1 ; |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
в) |
y x |
|
|
|
на интервале |
|
|
, 2 |
; |
|
|
|
|||||||||||||
|
x |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y cos2x на интервале |
|
|
|
|
|
|
|
|||||||||||||||||
г) |
|
|
, |
|
|
; |
|
||||||||||||||||||
4 |
3 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
д) |
y x sinx на интервале 0, 4 ; |
|
|||||||||||||||||||||||
е) |
y |
|
x2 6 |
|
x |
|
8 |
|
на интервале 1,1 . |
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
9.4.6. Найти точки перегибов функций: |
|
||||||||||||||||||||||||
а) y 5x 6 x2; б) y x4 13x2 36; в) y |
1 |
; |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
г) y e 2 ; д)y x2e x ; е) y ln 6x 8 x2 ; |
|
||||||||||||||||||||||||
ж) |
y sinx; з) y x cosx. |
|
|
|
|
|
|
|
|
||||||||||||||||
9.5. Приближенные методы нахождения корней уравнений
При исследовании свойств функции y f x необходимо на-
ходить: |
f x 0 – нули функции; |
|
– корни уравнения |
||
– корни уравнения |
|
– абсциссы критических точек |
f x 0 |
||
первого рода (стационарных точек), которые могут быть экстремумами;
– корни уравнения f x 0 – абсциссы критических точек второго рода – возможные точки перегиба функции.
Будем представлять все указанные уравнения одним уравнением вида x 0.
136
Для многих видов уравнений x 0 отсутствуют точные методы определения корней, поэтому широко используются приближенные методы, которые разделяют на две группы:
–методы отделения корней;
–методы уточнения корней.
Методы отделения корней позволяют в области существования (определения) функции y x выделить отрезки, внутри
которых содержится только один корень. В этом случае справедлива теорема Больцано – Коши: если непрерывная функция y x на концах отрезка , принимает значения разных знаков, т.е. 0, то внутри отрезка содержится, по край-
ней мере, один корень уравнения x 0.
Общего алгоритма отделения корней не существует. В зависимости от особенностей функции используют, по существу, различные частные графические, аналитические и вычислительные приемы выделения отрезков, внутри которых содержится один корень. После выделения такого отрезка , можно существен-
но уменьшить его длину до заданной точности методами уточнения корней. Наиболее простым из таких методов является метод половинного деления (дихотомии), который позволяет с помощью простого удобного алгоритма уточнить значения корня уравнения с любой наперед заданной точностью. При этом на отрезке выделения корня уравнения x 0 функция y x
должна быть непрерывной и иметь разные знаки на концах этого отрезка.
Рассмотрим методику уточнения корня с использованием метода половинного деления на конкретном примере.
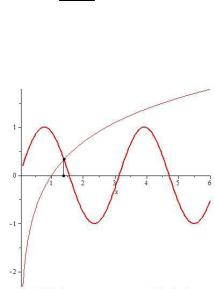
Пример. Найти корни уравнения sin2x lnx 0. Решение. Функция y sin2x – периодическая, а функция
y lnx – монотонно возрастающая, поэтому графики (рис. 9.21)
этих функций имеют единственную точку пересечения, которой соответствует нуль функции y sin2x lnx. Для отделения кор-
ня используем графический способ. Из графика следует, что значение корня лежит в промежутке 1; 1,5 . Таким образом, имеем
137
нулевое приближение |
1 |
|
1,5 1 |
1,25 (середина промежутка). |
|
||||
|
2 |
|
||
|
|
|
||
Точность 1 такого приближения равна половине длины проме-
жутка 1; 1,5 , т.е. 1 1,5 1 0,25. Корень лежит, вероятно, 2
внутри промежутка 1,25; 1,5 . Поверим эту гипотезу: y 1,25 sin2,5 ln1,25 0,5972 0,2231 0,82, y 1,5 sin3 ln1,5 0,14 0,41 0,27.
Рис. 9.21. Решение уравнения sin2x lnx 0
В крайних точках промежутка 1,25; 1,5 функция имеет раз-
ные знаки, поэтому за следующее приближение корня можно
принять |
середину |
отрезка |
1,25; 1,5 , |
т.е. 2 |
|
1,25 1,5 |
|
1,375, |
||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
1,5 1,25 |
|
|
|
|
2 |
|
|
|
точность которого равна: 2 |
|
0,125. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
Снова делим отрезок 1,25; 1,5 пополам и находим значение |
|||||||||||||||
функции |
y sin2x lnx в |
его середине: y 1,375 0,08. |
Таким |
|||||||||||||
образом, |
корень лежит на промежутке 1,375; |
1,5 . |
Его середина |
|||||||||||||
3 |
1,375 1,5 |
1,4375 |
– очередное приближение корня уравне- |
|||||||||||||
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
1,5 1,375 |
|
|
|
|
|
|
|
ния |
|
с |
точностью |
3 |
0,0625; |
при |
этом |
|||||||||
|
|
|||||||||||||||
y 1,4375 0,1. |
|
|
2 |
|
|
|
|
|
|
|
||||||
Значит, |
корень |
лежит |
на |
промежутке |
||||||||||||
138

1,375; 1,4375 и его середина |
4 |
|
1,375 1,4375 |
1,40625 – сле- |
|||
|
|||||||
|
|
2 |
|
1,4375 1,375 |
|
||
дующее приближение корня |
с |
точностью 4 |
|
|
|||
|
|||||||
|
|
|
|
2 |
|
||
= 0,03125. Продолжая процесс деления отрезка пополам, можно получить значение корня уравнения с любой заданной точностью.
Задачи к разделу 9.5
9.5.1.Уравнение x4 2x2 12x 8 0 имеет два действительных корня. Найти эти корни методом дихотомии с точностью до
0,01.
9.5.2.Уравнение x2 2x 5 2 2 x2 2x 5 x 5 имеет че-
тыре действительных корня. Найти эти корни методом дихотомии с точностью до 0,01.
9.5.3. Пользуясь методом дихотомии, найти корни следующих уравнений с точностью до 0,01:
а) x sinx 2; б) cosx x2 0; в) x ex 0. 10
9.5.4. Метод хорд приближенного решения уравнений состоит в следующем: пусть на промежутке , функция y x
имеет единственный корень и 0. Составляется урав-
нение прямой, проходящей через точки A ; и B ; и
находится точка A1 1, 1 пересечения этой прямой с осью абс-
цисс. По теореме Больцано – Коши определяется, на каком из промежутков , 1 или 1, находится корень уравнения, и
на этом промежутке снова строится аналогичная прямая. За последовательные приближения корня принимаются точки пересечения прямых с осью абсцисс, а за точность приближения – половина длины соответствующего промежутка приближения.
Спомощью метода хорд найти корни следующих уравнений
сточностью до 0,01:
а) x3 6x 2 0; б) x4 x 1 0.
139
9.6.Определение экстремальных значений функции
вприкладных задачах
Исследования экстремальных значений функции находят наиболее широкое применение в технических науках и инженерной деятельности.
Во многих случаях в прикладных задачах можно не использовать достаточные условия экстремума, а выбирать в качестве экстремальных значений те критические точки первого рода, которые соответствуют условиям прикладной задачи. Тогда достаточные условия экстремума можно использовать для проверки.
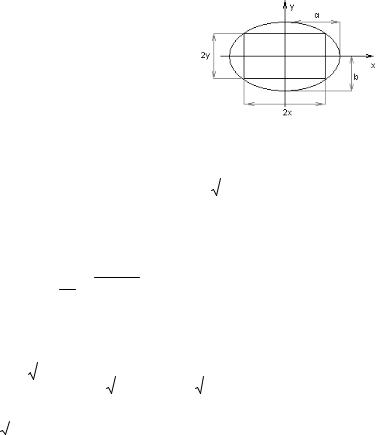
Пример 1. Из эллиптической заготовки (рис. 9.22) требу-
ется вырезать прямоугольную пла- |
|
|
|
|||||||||
стинку наибольшей площади. |
|
|
|
|
|
|
||||||
Решение. Обозначим неизвест- |
|
|
|
|||||||||
ные длины сторон искомой прямо- |
|
|
|
|||||||||
угольной пластинки 2x и 2y, тогда |
|
|
|
|||||||||
ее площадь |
будет равна |
|
S 4xy. |
|
|
|
||||||
Величины x |
и yсвязаны между со- |
|
Рис. 9.22. Эллиптическая |
|||||||||
бой уравнением эллипса |
x |
2 |
|
y |
2 |
1. |
|
|||||
|
|
|
|
заготовка |
||||||||
a2 |
b2 |
|||||||||||
|
|
|
|
b |
|
|
|
|||||
|
|
|
|
|||||||||
Из уравнения эллипса находим |
y |
|
a2 x2 |
(знак «+» перед |
||||||||
a |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
корнем выбран потому, что мы считаем длину стороны равной 2y, а длина по определению не может быть отрицательной), и
подставляем в уравнение площади прямоугольника. Тогда полу-
чаем S S x 4b x
 a2 x2 при 0 x a. Находим экстремумы a
a2 x2 при 0 x a. Находим экстремумы a
функции S x , для этого сначала определяем критические точки первого рода из необходимого условия экстремума S x 0:
|
|
4b |
|
|
x 2x |
|
|
|
1 |
2 2 2 |
|||
|
|
2 2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a x x 0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a x |
|
|
|||||||||
S x |
|
|
|
||||||||||
|
|
a |
|
|
|
2 a2 x2 |
|
|
|
a2 x2 |
|
||
|
|
|
|
|
|
|
|
|
|||||
x |
a |
(знак «+» выбран из тех же соображений, что и выше). |
|||||||||||
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
140
