
m0936
.pdf
Элементарные функции, полученные из табличных с помощью арифметических операций, будем называть составными. Для составных функций справедливы следующие правила дифференцирования (если правые части равенств имеют смысл):
1) u v w ... u v w ... – производная суммы конечного числа функций равна сумме производных;
2)u v u v uv ;
3)C u Cu , где C const, – постоянный множитель вы-
носится за знак производной;
4) uv
C
5) v
u v uv ;
v2
C
v2 , где C = const.
Примеры. Найти производные составных функций, используя табличные производные и правила дифференцирования:
а) y x 2 |
|
; б) y x2 cosx; в) |
y |
cosx |
. |
|
x |
||||||
|
||||||
Решение: |
|
|
1 sin x |
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а) |
y x |
2 x |
1 2 |
|
1 |
|
; |
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||
|
y x |
2 |
|
|
2 |
x |
|
x |
|
|
||||||||
б) |
x |
2 |
|
|
2xcosx x |
2 |
sin x; |
|||||||||||
cosx |
|
cosx |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
y cosx 1 sin x cosx 1 sin x |
|
|
|||||||||||||||
|
|
|
|
|
1 sin x 2 |
|
|
|
|
|
|
|
|
|
|
|||
|
sinx 1 sinx cosx cosx |
|
|
1 |
. |
|
||||||||||||
|
|
|
|
|||||||||||||||
|
|
1 sinx 2 |
|
|
1 sinx |
|
|
|||||||||||
|
|
|
|
|
Задачи к разделу 8.3 |
|
|
|||||||||||
8.3.1. Доказать, что если функция |
f x имеет производную в |
|||||||||||||||||
точке |
x0 , а |
функция |
|
g x |
– нет, |
|
то функции f x g x , |
|||||||||||
f x g x не имеют производных в этой точке.
81
8.3.2. Привести пример функции f x , имеющей производ-
ную на всей числовой прямой, и функции g x , не имеющей про-
изводной в точках x1, x2, , xn , но таких, что функция f x g x
имеет производную на всей числовой прямой.
8.3.3. Привести пример функций f x , g x , которые не име-
ют производных в точке x0 , но:
а) функция f x g x имеет производную в этой точке;
б) функция f x g x имеет производную в этой точке;
в) функция f x g x имеет производную в этой точке.
8.3.4.Используя формулу u v u v uv , доказать, что:
а) u v w u vw uv w uvw ;
б) f g h s f ghs fg hs fgh s fghs .
8.3.5.Найти производные следующих функций:
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
3x 1 |
|
||
а) |
y x |
|
|
|
|
; б) |
y xlnx x; в) |
y 3 |
; |
|||||||
|
x2 |
|||||||||||||||
г) |
y |
ex |
e x |
; д) |
y |
ex e x |
(гиперболический тангенс); |
|||||||||
|
|
2 |
|
|
ex e x |
|||||||||||
|
|
|
|
|
|
|
|
|
sinx |
|
|
|||||
е) |
y logx a, а = const; ж) |
y |
; з)y x sinx 2x. |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
8.4. Способы вычисления производных сложных функций
Для вычисления производных сложных функций используют различные способы, в основе которых лежит цепное правило дифференцирования.
Пусть дана сложная функция, которую можно разложить на табличные функции при ведении промежуточных аргументов:
y f x u x , v u , yv f v ,
где x – основной аргумент (независимая переменная); u, v – про-
межуточные аргументы. Промежуточные аргументы являются функциями независимой переменной x u u x ,v v x . После разложения производную сложной функции находят, используя цепное правило:
82

yx yv vu ux .
Рассмотрим способы вычисления производных сложных функций.
Первый способ (классический) основан на предварительном полном разложении сложной функции на табличные функции с явным введением промежуточных аргументов. Затем используется цепное правило.
Пример 1. Найти производную yx для функции y arcsin
 1 4x.
1 4x.
Решение.
1. Разбиваем сложную функцию на табличные с введением промежуточных аргументов:
yarcsin
 1 4x [u 1 4x,v
1 4x [u 1 4x,v 
 u, yv arcsinv].
u, yv arcsinv].
2.Дифференцируем табличные функции по промежуточным
аргументам и затем переходим к основному аргументу:
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ux |
1 4x 4 |
; vu |
|
u u |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||
|
u |
1 4x |
||||||||||||||||||||||||
yv |
arcsinv v |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 v2 |
|
|
|
|
|
|
|
2 |
2 x |
|||||||||||||||||
|
|
|
|
|
1 |
1 4x |
|
|
|
|
|
|||||||||||||||
3. Перемножаем производные табличных функций, используя цепное правило, и получаем окончательный результат:
yx yv |
vu |
ux |
|
|
1 |
|
|
1 |
|
|
|
4 |
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
1 4x |
x |
1 4x |
|
||||||||||||||||||||||||
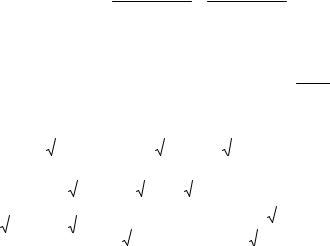
Пример 2. Найти производную yx |
для функции |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
y arctg2 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||
Решение. Если опустить описания этапов, то объем вычисле- |
||||||||||||||||||||||||||||
ний можно сократить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
arctg |
|
|
|
|
|
|
|
|
, v arctgu, yv v |
ux vu |
yv |
|
|||||||||||||||
y |
|
u |
|
x |
||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
83
|
|
1 |
1 |
1 |
|
1 |
|
1 |
|
2arctg |
1 |
|
|
||||
|
|
|
|
x |
|||||||||||||
|
|
|
|
|
|
2v |
|
|
|
|
2arctg |
|
|
|
. |
||
|
|
|
|
1 |
|
|
|
||||||||||
|
|
x2 |
|
1 u2 |
|
x2 |
1 |
|
x |
x2 1 |
|||||||
|
|
x2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второй способ (переход от простого к сложному). Этот способ заключается в том, что сначала выделяют табличную функцию с основным аргументом и дифференцируют ее. Затем эту функцию принимают за промежуточный аргумент, выделяют следующую табличную функцию с этим аргументом и дифференцируют по этому аргументу и т.д. Промежуточные аргументы обычно не вводят в явном виде.
Пример 1. Найти производную функции y arctg ln sin x3 .
Решение:
|
|
|
|
|
|
|
x3 u, sin x3 v, ln sin x3 w |
|||
y arctgln sin x3 |
||||||||||
x3 |
|
sin x3 |
ln sin x3 |
arctg ln sin x3 |
||||||
x |
|
|
|
u |
|
|
v |
|
w |
|
3x |
2 |
cosx |
3 |
|
|
1 |
1 |
|
3x2 ctgx3 |
|
|
|
|
|
|
1 ln2 sinx3 |
1 ln2 sinx3 . |
||||
|
|
sinx3 |
||||||||
Явное указание промежуточных аргументов целесообразно опускать, выполняя их в уме. Это существенно сокращает вычисления.
Пример 2. Найти производную функции y sin2 
 1 x2 .
1 x2 .
Решение:
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
||||
|
sin 1 x |
|
|
|
2sin 1 x |
sin |
|
1 x |
|
|
|
|
|||||||||||||||
y |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2sin |
1 x2 |
|
cos |
1 x2 |
1 x2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
xsin |
2 |
|
1 |
x |
|
||||||
2sin |
1 x2 cos |
1 x2 |
|
|
1 x2 |
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 1 x2 |
|
|
|
|
|
1 x2 |
|
|
|||||||||
Если сложные функции связаны между собой арифметическими операциями, то получаем сложносоставную функцию, при вычислении производной которой дополнительно используют правила дифференцирования, аналогичные указанным выше.
84

Пример.
Решение:
Найти производную функции y sinx2 . tg x
x
y sin x2 tg
 x sin x2 tg
x sin x2 tg
 x tg2
x tg2 
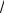 x
x
2xcosx2 tg |
|
sinx2 |
1 |
1 |
|
|
|
|||||
x |
||||||||||||
cos2 |
|
|
|
|
|
|
||||||
x 2 x |
|
|||||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||
|
|
tg2 x |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
2x
 xcosx2 sin2
xcosx2 sin2
 x sinx2 . 2
x sinx2 . 2
 xsin2
xsin2 
 x
x
Замечание. Для правильного вычисления производных сложных функций необходимо хорошее знание таблицы производных и устойчивые навыки разложения сложной функции на табличные. При этом необходимо владеть двумя способами вычислений, чтобы один из способов использовать для проверки правильности вычислений.
Задачи к разделу 8.4
8.4.1. Найти производные функций:
|
y lncosx; б) y |
1 |
|
|
x |
, a const; в) |
|
|
x2 |
|
||||||||
а) |
arctg |
y e 2 |
; |
|||||||||||||||
a |
a |
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
г) |
y |
|
; д) |
y 5 |
|
; е) |
y |
|
|
; |
|
|
||||||
|
cosx |
|
|
|||||||||||||||
ln2 |
|
|
|
|
|
|
||||||||||||
|
|
x |
|
|
|
|
|
|
|
4 arcsinx 3 |
|
|
||||||
ж) y eex ; з) y 2x2 . |
|
|
|
|
|
|
|
|
|
|
||||||||
8.4.2. Найти |
тремя |
способами |
производную |
функции |
||||||||||||||
yarctg3
 x .
x .
8.4.3.Найти производные функций:
а) |
y 2lnsin x ; б) y 2sinln x ; в) y sin2ln x ; |
г) |
y sinln2x ; д) y lnsin2x ; е) y ln2sin x. |
8.4.4. Найти производные функций:
а) y sin sin sin x ; б) y 
 x
x 
 x
x 
 x ; в) y ln x ln x lnx ; г) y 2x 2x 2 .
x ; в) y ln x ln x lnx ; г) y 2x 2x 2 .
85

8.4.5. Найти производные функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ln 1 x2 ; б) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
а) |
y xarctgx |
y xarcsinx |
|
1 x2 |
; |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ln x |
|
|
|
, a const; |
||||||||||
|
|
|
1 |
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
в) |
y |
ln |
|
, a const; г) |
x2 |
a2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2a |
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
д) |
y |
|
|
a2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
8.4.6. Найти производные функций: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
а) |
y |
1 |
|
ln |
|
|
|
x 1 2 |
|
|
1 |
|
arctg |
2x |
|
1 |
; |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
x2 x 1 |
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
б) |
y |
1 |
ln |
|
x 1 |
|
1 |
arctgx; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
x 1 |
2 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
в) |
y |
1 |
|
|
|
|
ln |
1 x |
|
|
3 |
|
1 |
arctgx |
1 |
arctgx3. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
4 3 1 x 3 x2 |
2 |
|
|
|
6 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
8.5. Логарифмическое дифференцирование
Способ вычисления производной, при котором функцию сначала логарифмируют, а затем дифференцируют как сложную функцию, называется логарифмическим дифференцированием:
y y x ln y x ln y x x ;
yx |
ln y x x yx |
y ln y x x . |
|
y |
|||
|
|
При логарифмическом дифференцировании удобнее не использовать приведенную выше готовую формулу, а выполнять последовательно операции логарифмирования и дифференцирования.
Логарифмическое дифференцирование целесообразно использовать при вычислении производной функции, содержащей в своем составе произведения и отношения других функций, а также для вычисления производных показательно-степенных функций вида y f x x .
86

Пример 1. Найтипроизводнуюфункции y |
|
|
|
2x 4 |
|
4x 1 |
|
|
. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
2x 1 33 x3 2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ln y ln2x ln4 |
|
|
|
|
|
|
ln 2x 1 3 |
|
ln3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x3 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
4x 1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
xln2 |
1 |
|
ln 4x 1 3ln 2x 1 |
1 |
|
x3 2 ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
||||||||||||||
ln y |
|
xln2 |
|
|
|
|
ln 4x 1 3 ln 2x |
1 |
|
x |
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
4 |
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ln2 |
|
1 |
|
|
|
|
|
|
|
6 |
|
|
|
|
x |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
4x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 1 x3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
x2 |
|
|
|||||||||||||||||||||
|
|
|
|
4x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln2 |
|
|
|
|
|
2x 1 |
x |
1 |
. |
|
|
||||||||||||||||||||||||||||||
|
|
|
2x 1 33 x3 2 |
|
|
|
|
|
|
|
|
4x 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Пример 2. Найти производную функции y xarctgx . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctgx |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln y |
|
lnx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
arctgx |
ln x arctgx lnx |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
y x |
arctgx |
|
|
|
lnx |
|
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
При дифференцировании |
|
|
|
показательно-степенной |
|
функции |
|||||||||||||||||||||||||||||||||||||||||||||||||||
используют также второй способ, основанный на представлении
этой |
функции |
в |
виде |
показательной |
функции |
y f x x e x ln f x |
и |
последующем ее дифференцировании |
|||
как сложной функции.
Этот способ, по существу, является разновидностью первого способа, так как при выводе формулы y f x x e x ln f x ис-
пользуется логарифмирование или равносильные ему действия.
Пример. Найти производную функции y xarctgx .
Решение:
y xarctgx earctgx ln x;
87

|
arctgx ln x |
|
arctgx ln x |
lnx |
|
arctgx |
|
arctgx |
lnx |
|
arctgx |
||
y e |
|
e |
|
|
|
|
|
x |
|
|
|
|
. |
|
1 x2 |
x |
1 x2 |
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
Задачи к разделу 8.5
8.5.1. Используя логарифмическое дифференцирование, найти производные функций:
|
x2 3x 510 x2 6x 18 |
3 |
|
|
|
4 |
|
|
|
|
||||||||
а) y |
2x 3 |
|
3x 4 |
|
|
|||||||||||||
|
|
|
|
|
|
; б)y |
|
|
|
|
|
; |
||||||
x2 5x 2 12 x2 4x 3 9 |
5 |
|
|
|
|
|
||||||||||||
4x 5 |
5x 6 |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x2earctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x2 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) y |
x |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 x3 x2 |
x 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8.5.2. Используя логарифмическое дифференцирование, найти производные функций:
|
x |
|
|
x |
2 |
|
1 |
x |
|
|
|
|
|||||||
а) y x |
|
; б) y |
x |
|
; в) y 1 |
|
|
; |
|
|
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
г) y x2 3x 4 x2 4x 5; д) y xxx .
8.6. Вычисление производных высших порядков
Производной второго порядка функции y y x называется производная от ее производной. Производной третьего порядка называется производная от ее второй производной. Производной четвертого порядка называется производная от ее третьей производной.
Замечание. Аналогично можно определить производные любого по-
|
|
|
|
|
|
|
4 |
|
|
|
|
|
y n x y |
|
|
рядка: |
x |
y |
n 1 x |
; … . |
|||||||||||
y |
x y x ; |
y x y |
x ; y |
|
|
x ; …; |
|
|
|||||||
В соответствии с определением производные второго, третьего и более высоких порядков вычисляют последовательным дифференцированием производных предыдущих порядков. При этом используются те же табличные производные и правила дифференцирования, которые применялись для вычисления производных первого порядка.
88

Пример. Найти производную второго порядка функции
|
|
|
|
|
|
|
|
|
|
|
|
|
y arctg |
|
|
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
4 x2 |
|
|
|
|
|
4 x2 |
x |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 4 x2 |
|||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
x |
|
|
|
|
|
|
4 x |
x |
|
|
|
|
4 x |
|
|
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
4 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
4 x2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y |
|
|
|
|
|
4 x2 |
2 |
|
|
|
2x |
|
|
|
|
|
. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
4 x2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x2 4 x2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Задачи к разделу 8.6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
8.6.1. Найти y для функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ln cosx . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x 3 x3 |
|
|
|
|
|||||||||||||||||
а) |
y xlnx x; б) y e |
2 ; в) |
|
1; г) |
||||||||||||||||||||||||||||||||||||||
8.6.2. Найти производные десятого порядка функций: |
||||||||||||||||||||||||||||||||||||||||||
а) y x9 3x7 5x5 7x3 9x; б) y ex ; в) y 2x ; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
г) |
y sinx; д) |
|
y cos2x; е) |
y lnx; ж) |
y loga x, a const. |
|||||||||||||||||||||||||||||||||||||
8.6.3. Вывести формулы для нахождения производных любо- |
||||||||||||||||||||||||||||||||||||||||||
го порядка функций: а) |
y ex ; б) |
|
y ax; в) |
y sinx; г) |
y cosx; |
|||||||||||||||||||||||||||||||||||||
д) y lnx; е) y loga x, a const; |
ж) |
y x . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
8.7. Дифференцирование параметрически заданных функций
Функция в параметрической форме представляется так:
x x t ,
y y t ,
где t – переменный параметр (переменная, равномерно изменяющаяся скалярная величина). В прикладных задачах обычно t – текущее время.
Производные параметрически заданных функций определяются по формулам:
89
|
|
|
|
|
|
y t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
yx |
|
|
|
|
|
|
|
|
; |
|
yx yx t |
|
|
|
|
|
; |
|
yx |
|
yx t |
|
|
|
|
|
|
; … |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример. Найти yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
для функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
t. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
|
3 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
t |
2 |
1 |
|
|
|
1 |
|
|
t |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
t |
2 |
1 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
; |
|
|
|||||||||||||||||
|
yx |
|
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4t |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
2t |
2 2t |
t |
|
|
2t |
|
|
|
|
2 2t |
|
|
|
|
|
2t |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
t2 |
1 |
|
|
|
|
1 1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 1 |
|
|
|
|
t2 3 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
5 . |
|||||||||||||||||||||||||||
yx |
|
|
|
|
|
2t |
|
|
|
|
4t |
|
2t |
|
|
|
|
|
|
|
4t |
|
8t |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
4t |
|
|
t |
|
|
|
|
|
4t |
|
|
|
|
t |
|
|
|
|
|
|
|
4t |
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи к разделу 8.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
8.7.1. Найти yx |
|
для параметрически заданных функций: |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x cos2 t, |
|
б) |
|
x acos t |
(эллипс); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
y sin2 t; |
|
|
|
|
|
|
|
y bsin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
t |
e |
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x a t sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
(циклоида); г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
(гипербола); |
|||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
et |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
y a 1 cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x Rcos3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
4 |
|
(астроида). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
д) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
y Rsin3 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4
8.7.2. Найти yx и yx |
для параметрически заданных функций: |
||
x 2t 3, |
x cost |
||
а) |
б) |
(окружность); |
|
y 3t 4; |
y sint |
||
x a t sint |
(циклоида). |
||
в) |
|
||
y a 1 cost |
|
|
|
90
