
m0936
.pdf
8.7.3. Считая параметр t положительным, изобразить в прямоугольной системе координат линии из задачи 8.7.1:
а) определить, сколько различных непрерывных функций задает каждая из этих линий;
б) определить, в каких точках этих линий производная бесконечна и в каких не существует.
8.8. Производные неявных функций
Неявной функцией будем называть функцию, представленную в виде уравнения с двумя аргументами F x, y 0. При этом один аргумент считается функцией другого аргумента y y x .
Для нахождения производной функции y y x , заданной
как неявная функция, необходимо продифференцировать обе части равенства F x, y 0 и выразить y из полученного уравне-
ния. При этом в процессе дифференцирования выражения F x, y
необходимо учитывать, что переменная y сама является функцией.
|
|
d |
F x, y 0 x, y, y 0. |
(8.1) |
|
|
|
||
|
|
dx |
|
|
Из (8.1) находим первую производную неявной функции в |
||||
явном виде yx |
x,y . |
|
||
При нахождении второй производной дифференцируют ра-
венство |
yx x,y как сложную функцию, |
в результате полу- |
|||||||||||||||||||||||||||||||||||
чают yx |
x, y, y x, y, x, y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
y |
|
Пример. Найти yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 |
||||||||||||||
для неявной функции |
e x . |
||||||||||||||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x2 |
y2 |
arctg |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
x arctg |
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
2 x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2x 2yy |
|
e |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
yx y; |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|||
|
2 |
|
|
x2 y2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
yy |
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x2 y2 |
|
|
|
|
|
|
|
yx y |
; |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 y2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||||
91

x yy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x |
; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
yx y; |
y y x y x; y |
|
x y |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
x y |
|
x y x y x y x y |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x y 2 |
|
|
|
|
|
|
|
|||||||||
x |
|
x y |
|
|
|
|
2xy |
|
2y |
|
||||||||||||
|
|
1 y |
x y x y 1 y |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y 2 |
|
|
2 x |
x y 2 |
|
|
||||||||||
|
|
|
|
|
2 |
|
|
x y |
|
|
2 y2 |
|
|
|
|
|||||||
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
. |
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
x |
y |
|
|
x y |
|
|
|
x |
y |
|
|
|
|
|||||
|
|
|
|
|
|
Задачи к разделу 8.8 |
|
|
|
|
|
|
|
|
||||||||
8.8.1. Не |
|
любое уравнение вида F x, y 0 |
задает какую- |
|||||||||||||||||||
либо функцию. |
Убедиться в |
этом |
|
|
на |
примере уравнения |
||||||||||||||||
x2 y2 1 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.8.2. Уравнение может не задавать ни одной функции, может задавать единственную непрерывную функцию и может задавать несколько (даже бесконечно много) непрерывных функций. Изобразив, если это возможно, в системе координат заданную линию, определить, сколько непрерывных функций задает ее уравнение (считая область определения совпадающей с областью существования):
|
|
|
|
|
|
|
|
arctg |
y |
x |
2 |
|
|
y |
2 |
|
|
x |
2 |
|
y |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а) |
|
x2 y2 e |
|
x 0; б) |
|
|
|
|
1; в) |
|
|
|
1; |
||||||||||||||||
|
|
a2 |
b2 |
a2 |
b2 |
||||||||||||||||||||||||
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
г) |
0; д) x sin y 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
8.8.3. Найти yx |
для неявно заданных функций: |
|
|
||||||||||||||||||||||||||
а) |
x2 y2 |
R2; б) x3 y3 3xy 0 (декартов лист); |
|||||||||||||||||||||||||||
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в) |
x |
3 |
y |
3 |
R |
3 |
|
(астроида). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8.8.4. Найти yx |
для неявно заданных функций: |
|
|
||||||||||||||||||||||||||
|
|
|
|
y |
; б) x2 |
y2 |
|
|
|
|
|
||||||||||||||||||
а) |
|
x2 y2 |
arctg |
|
x2 y2 |
|
x. |
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
92

8.8.5. Найти yx для неявно заданных функций:
2 2 2
а) x2 y2 R2; б) x3 y3 R3 .
8.9. Вычисление пределов функций с помощью производных (правило Бернулли – Лопиталя)
Правило Бернулли – Лопиталя используют для раскрытия не-
определенностей вида |
0 |
или |
|
|
при вычислении пределов |
|||
|
|
|
|
|
|
|||
0 |
|
|||||||
|
|
|
|
|
|
|
||
функций. С помощью этого правила вычисление предела отношения функций сводится к пределу отношения производных этих функций:
lim |
f x |
|
|
0 |
или |
|
|
lim |
f x |
. |
|
|
|
|
|
|
|||||||
g x |
|
0 |
|
|
|||||||
|
|
|
|
|
g x |
||||||
x a |
|
|
|
|
|
|
|
x a |
|
||
|
|
|
|
|
|
|
|||||
При этом должны выполняться следующие условия:
– функции f x и g x должны быть определены и диффе-
ренцируемы в некоторой проколотой окрестности предельной точки x a (или соответственно в окрестности бесконечности), при этом
lim |
f x |
lim g x 0; |
x a |
|
x a |
– в любой достаточно малой окрестности точки x a производная функции g x не обращается в ноль: g x 0.
При вычислении пределов функций с помощью правила Бернулли – Лопиталя необходимо учитывать, что:
–правило можно использовать многократно, используя повторное дифференцирование;
–для раскрытия неопределенностей других видов функцию под знаком предела необходимо привести с помощью тождест-
|
|
|
0 |
|
|
|
|||
венных преобразований к виду |
|
|
|
или |
|
|
. |
||
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Пример 1. Найти lim |
|
arctgx lnx. |
|||||||
2 |
|||||||||
x |
|
|
|
|
|
|
|
||
93

Решение:
|
|
|
|
arctgx |
|
0 |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
||||||||||
lim |
|
arctgx lnx 0 lim |
|
|
|
|
|
|
|
. |
|
|
|
|||
|
1 |
|
|
|
|
|
|
|||||||||
x 2 |
|
x |
|
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
lnx |
|
|
|
|
|
|
0 |
|||
После преобразования неопределенности 0 к виду |
||||||||||||||||
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
можно использовать правило Бернулли – Лопиталя:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xln2 x |
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
lim |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
x 1 x2 |
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln2 |
|
x |
x |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
xln2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x 2xlnx |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
lim |
x |
lim |
|
|
x |
|
|
|
|
|||||||||||||||||||||||
|
|
|
1 x |
2 |
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
||||||||||||||||
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
2ln x |
1 |
2 |
1 |
|
|
|
|
|
ln x |
|
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||
lim ln |
|
x 2ln x |
lim |
|
|
|
|
x |
|
|
|
|
|
lim |
1 |
lim |
0. |
||||||||||||||||||
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
|
|
|
|
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
x |
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
После четырехкратного дифференцирования неопределенность раскрыта и предел вычислен.
9
Пример 2. Найти lim
x 0 x
Решение:
4 ex 1 .
|
9 |
|
|
|
4 |
|
|
|
|
9 ex |
|
|
|
|
|
0 |
|
|||||
|
|
|
|
lim |
1 4x |
|
|
|||||||||||||||
lim |
|
|
|
|
|
|
|
x ex |
|
|
|
|
|
|
||||||||
|
|
x |
|
|
|
|||||||||||||||||
x 0 |
x |
|
e |
1 |
|
|
|
x 0 |
|
|
0 |
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
lim |
|
|
9ex 4 |
|
|
5 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x 0 e |
|
x 1 1 |
|
|
|
|
|
|
|
|
||||
Понятно, что если предел существует, то он равен либо ,
либо . Но, поскольку lim |
|
|
9ex 4 |
|
5 |
|
, |
||
|
|
|
|
|
|
|
|||
|
x |
x 1 1 |
0 |
||||||
x 0 e |
|
|
|
|
|
||||
94

а lim |
|
|
9ex 4 |
|
5 |
|
, то данный предел не существует. |
||
|
|
|
|
|
|
|
|||
|
x |
x 1 1 |
0 |
||||||
x 0 e |
|
|
|
|
|
||||
При нахождении предела показательно-степенной функции y f x x , если имеет место неопределенность, предварительно используют логарифмирование, а затем тождественные математические преобразования, приводящие к неопределенности вида
0 |
|
|
|
|||
|
|
|
или |
|
|
. |
|
0 |
|
|
|
|
|
3
Пример 3. Найти lim cos2x x2 .
x 0
Решение:
3
lim cos2x x2 1 A.
x 0
Принимаем, что предел имеет некоторое конечное значение A, и логарифмируем обе части равенства:
3 |
|
3 |
|
||
ln A lnlim cos2x |
|
lim |
lncos2x. |
||
x2 |
|||||
|
|||||
x 0 |
x 0 x2 |
|
|||
Используя свойство предела функции, меняем местами операции логарифмирования и предела. Затем логарифмируем функцию под знаком предела и вычисляем предел, используя правило Бернулли – Лопиталя.
3lim lncos2x
x 0 x2
3lim
x0
Поскольку
|
0 |
|
|
|
|
|
|
|
1 |
2sin2x |
||||
|
|
|
|
|
|
cos2x |
||||||||
|
3lim |
lncos2x |
3lim |
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
x 0 |
|
|
x 0 |
|
2x |
||||||||
|
0 |
|
|
|
x2 |
|
|
|
|
|||||
tg2x |
|
|
|
|
|
|
|
1 |
2 |
|||||
|
|
|
|
|
cos2 2x |
|||||||||
3lim |
tg2x |
3lim |
|
6. |
||||||||||
|
x |
|
|
x 0 |
x |
|
x 0 |
1 |
|
|
|
|||
ln A 6, то A e 6 .
Второй способ вычисления предела показательно-степенной функции основан на использовании тождества
lim |
f x x |
|
lim e x ln f x . |
x a |
|
|
x a |
95
Пример. Найти lim xtgx .
x 0
Решение:
|
|
|
lim xtgx lim etgxln x |
lim tgxln x |
; |
|
|
||||||||
|
|
|
ex 0 |
|
|
|
|||||||||
|
|
|
x 0 |
x 0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
limtg xln x 0 lim |
ln x |
|
|
||||||||||||
ctgx |
|
||||||||||||||
x 0 |
|
|
x 0 |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
sin2 |
x |
|
|
2sinxcosx |
|
|||||
lim |
|
|
x |
|
|
lim |
lim |
0. |
|||||||
1 |
|
|
|
|
|||||||||||
x 0 |
|
x 0 x |
|
|
x 0 |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, lim xtgx e0 |
1. |
|
|
|
|
|
|
||||||||
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|||
Задачи к разделу 8.9
8.9.1. Вычислить пределы, используя правило Бернулли – Лопиталя:
а) |
lim |
|
ax 1 |
; б) lim |
log |
a |
x 1 |
; в) lim |
1 x |
1 |
; |
|
|
|
|||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
x |
|
|
|
xa |
|
|||||||||||||
г) |
lim |
sinax |
; д) |
lim |
|
lnx |
; е) |
lim |
lnx |
при 0; ж) lim |
. |
||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
x 0 sinbx |
|
|
x |
|
|
|
|
|
|
x x |
|
|
|
|
|
|
|
|
x ax |
|
||||||||||||||||||||||
8.9.2. Вычислить пределы, используя правило Бернулли – |
|||||||||||||||||||||||||||||||||||||||||||
Лопиталя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
tg x x |
|
|
|
|
|
|
|
|
|
tgx x |
x3 |
|
|
|
|
|
|
cosx 1 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
а) |
lim |
; б) lim |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
; в) |
lim |
; |
|
|||||||||||||||||||
|
x 0 |
|
x sin x |
|
|
x 0 |
|
x |
1 |
|
x |
3 |
|
sin x |
|
|
x 0 ex e x 2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
cosx |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
1 |
. |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx |
|
|
|
|
|
|
||||||||||||||||||||
г) |
lim |
|
2 |
|
|
|
; д) lim |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x 0 ex e x 2 x2 |
|
|
|
|
|
x |
|
|
2sin2 x 1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.9.3. Вычислить пределы, используя правило Бернулли – |
|||||||||||||||||||||||||||||||||||||||||||
Лопиталя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim lnxln 1 x ; б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
а) |
lim ctgx |
|
|
|
; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
x 1 0 |
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
96
в) lim |
|
1 |
|
1 |
|
|
lim |
|
1 |
|
1 |
|
|
|
|
|
; г) |
|
|
|
. |
||||
|
ex e2 |
|
|
|||||||||
x 2 0 x 2 |
|
|
|
x 1 0 lnx |
|
1 x |
||||||
8.9.4. Вычислить пределы, используя правило Бернулли – Лопиталя:
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
x |
e |
x |
x |
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
lim x |
x |
|
|
|
|
|
|
e |
|
|
|
|
||||||
а) |
|
; б) |
lim 1 |
|
|
; в) lim |
|
x |
|
|
; |
||||||||
|
x |
|
e |
x |
|||||||||||||||
|
x 0 |
|
|
|
|
x |
|
x e |
|
|
|
|
|||||||
|
|
|
|
1 |
x |
|
|
|
|
|
tg2x |
|
|
|
|
|
|
|
|
г) |
lim ln |
|
|
; д) lim tg x |
. |
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
||||||||||||
|
x 0 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
8.10.Некоторые геометрические приложения производных
8.10.1.Определение уравнений касательной и нормали к кривой
Уравнение касательной в точке M0 x0, y0 к графику гладкой функции y f x имеет вид:
y y0 k x x0 ,
где k tg 0 f M0 – угловой коэффициент касательной, 0 –
угол между касательной и положительным направлением оси абсцисс (см. рис. 8.1).
Уравнение нормали можно представить так:
1
y y0 f M0 x x0 .
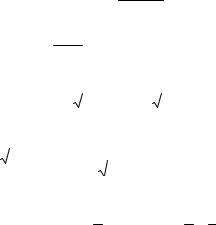
Пример 1. Найти уравнения касательной и нормали к гра-
фику функции y 
 x 5 в точке M0 с абсциссой x0 1.
x 5 в точке M0 с абсциссой x0 1.
Решение. Находим значение функции в точке x0 1:
|
|
|
|
|
y0 |
x 5 |
1 5 2. |
||
|
|
x 1 |
||
Находим угловой коэффициент касательной:
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
k y x0 |
x 5 |
|
|
|
|
|
. |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
x x0 |
|
2 x 5 |
|
x 1 |
4 |
|
||
|
|
|
|
|
|||||||
Тогда уравнение касательной в точке M0 1; 2 имеет вид:
y 2 1 x 1 y x 9. 4 4 4
97
Для построения касательной (рис. 8.3) находим координаты еще одной точки (например,
9 |
|
9 |
|
|
|
|
||
при x 0): y |
|
, M1 0; |
|
|
. |
|
|
|
|
4 |
|
|
|
||||
4 |
|
|
|
|
|
|||
Аналогично |
находим |
|
|
|
||||
уравнение нормали (рис. |
8.3) |
|
|
|
||||
в точке M0 1; 2 : |
|
|
|
|
|
|
||
y 2 4 x 1 y 4x 2. |
|
|
|
|||||
Для построения нормали |
Рис. 8.3. Касательная и нормаль |
|||||||
также найдем вторую |
точку |
|||||||
на этой прямой: |
N1 0; 2 . |
к графику функции y |
x 5 |
|
||||
Замечание. Для построения прямой (в частности касательной или нормали) достаточно знать коорди-
наты двух точек; для построения кривых обычно необходимо найти координаты не менее трех точек.
Пример 2. |
Найти |
||
уравнения |
касательной |
и |
|
нормали к неявно |
заданной |
||
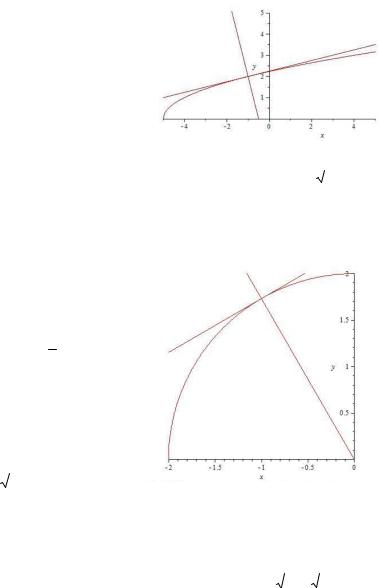
функции |
x2 y2 4 0 |
в |
|
точке M0 1; 
 3 .
3 .
Решение. Уравнение x2 y2 4 0 задает окруж-
ность радиуса R 2 с центром в начале координат (рис. 8.4), координаты точки
M0 1; |
|
|
|
удовлетворяют |
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
Рис. 8.4. Касательная и нормаль к |
|||||||||||||||||
этому уравнению. |
|
||||||||||||||||||
|
графику функции |
x2 y2 |
4 0 |
||||||||||||||||
Находим |
угловой |
коэф- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
фициент касательной: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
2 |
|
|
|
|
x |
|
1 |
|
|
1 |
|
||||
x |
|
y |
|
|
4 |
0 y |
|
, y M0 |
|
|
|
|
|
|
. |
||||
|
|
y |
|
|
|
|
|
||||||||||||
|
|
3 |
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
98
Уравнение касательной: |
y |
|
|
|
|
|
|
1 |
x 1 y |
x |
|
4 |
. |
||||
|
|
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
3 |
3 |
|
|||||||||||
Для построения касательной в точке M0 |
находим координаты |
||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|||||||
второй точки касательной: M1 |
0; |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
 3
3
Уравнение нормали: y 
 3
3 
 3 x 1 y
3 x 1 y 
 3x. Вторая точка нормали – N1 0; 0 .
3x. Вторая точка нормали – N1 0; 0 .
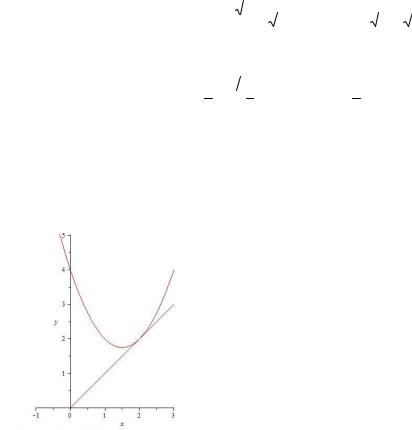
Пример 3. Парабола y x2 bx c касается прямой y x
в точке x0 2. Найти числовые значения параметров b и c.
Решение. Из уравнения прямой, касательной к параболе, оп-
ределяем ординату точки касания: y0 x0 2, |
M0 2; 2 . |
|
||||||||||
|
|
|
|
|
|
Для определения двух не- |
||||||
|
|
|
|
|
известных |
параметров |
имеем |
|||||
|
|
|
|
|
два условия: |
1) точка M0 2; 2 |
||||||
|
|
|
|
|
лежит на параболе; 2) произ- |
|||||||
|
|
|
|
|
водная функции y x2 bx c |
|||||||
|
|
|
|
|
совпадает с тангенсом угла на- |
|||||||
|
|
|
|
|
клона прямой y x |
к положи- |
||||||
|
|
|
|
|
тельному |
направлению |
оси |
|||||
|
|
|
|
|
абсцисс tg45 1 , рис. 8.5. |
|||||||
|
|
|
|
|
|
Из первого условия следу- |
||||||
Рис. 8.5. Касательная к графику ет: 4 2b c 2, из второго – |
||||||||||||
функции |
y x |
2 |
bx c |
x2 bx |
|
|
|
1 |
||||
|
||||||||||||
|
c |
|
x 2 |
|||||||||
|
|
2x b |
|
x 2 1 4 b 1. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Решая |
систему уравнений |
4 2b c 2, |
получим |
|||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
4 b 1, |
|
|
||||
b 3, c 4. |
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение параболы имеет вид: |
y x2 3x 4. |
|
|
|||||||||
99
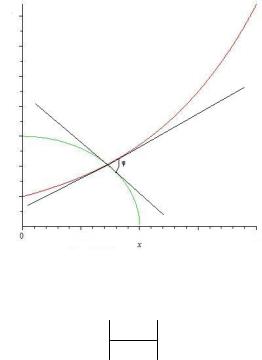
8.10.2. Определение угла между пересекающимися кривыми
Углом между кривыми в точке их пересечения называется угол между касательными к этим кривым в той же точке
(рис. 8.6).
Рис. 8.6. Угол между кривыми
При определении данного угла используют формулу для вычисления тангенса угла между прямыми
tg k1 k2 , 1 k1k2
где k1, k2 – угловые коэффициенты касательных как прямых,
представленных в виде: y k1x b1, y k2x b2.
Если известны уравнения кривых y y1 x , |
y y2 x и точка |
||||||
их пересечения M0 x0, y0 , то, учитывая, что k1 |
tg 1 y1 M0 , |
||||||
k2 tg 2 |
|
M0 , получим |
|
||||
y2 |
|
||||||
|
|
|
y1 M0 y2 M0 |
|
|
|
|
|
|
tg |
|
|
. |
|
|
|
|
1 y1 M0 y2 M0 |
|
||||
|
|
|
|
|
|||
Замечание. Данная формула справедлива и в тех случаях, когда уравнения кривых заданы в неявной и (или) параметрической форме.
100
