
m0936
.pdfСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ПРАКТИКУМ ПО ВЫСШЕЙ МАТЕМАТИКЕ
ДЛЯ ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ
Часть II
НОВОСИБИРСК
2014
УДК 51:001.4 ББК 22.1я73 П691
Практикум по высшей математике для технических
П691 специальностей /И. А.Вылегжанин, А.В. Пожидаев, П. И. Остроменский, Л. Г. Шандаров. – Новосибирск :Изд-во СГУПСа, 2014. – Ч. II. – 290 с.
ISBN 978-5-93461-633-6 (ч. II) ISBN978-5-93461-614-5
Представлены следующие темы высшей математики: основы теории пределов последовательностей и функций, основы дифференциального исчисления, неопределенный интеграл, которые изучаются на практических занятиях и самостоятельно во втором семестре первого курса большинства технических специальностей.
Предназначен для студентов технических специальностей, изучающих строительство зданий и сооружений, железных и автомобильных дорог, эксплуатацию подъемно-транспортных, строительных и дорожных машин, а также транспортного оборудования.
УДК 51:001.4
ББК 22.1я73
Утвержден к изданию на заседании редакционно-издательского совета университета.
Ответственный редактор канд. физ.-мат. наук, доц. В.В. Вдовин
Р ец ен з ен т ы:
кафедравысшейматематикиНГУЭУ(завкафедройканд.физ.-мат.
наук, доц. Ю.Н. Владимиров)
завкафедрой прикладной математики НГТУ д-р техн. наук, проф.
Ю.Г. Соловейчик, д-р техн. наук М.Э. Рояк
ISBN 978-5-93461-633-6 (ч.II) ISBN 978-5-93461-614-5
Сибирский государственный университет путей сообщения, 2014
Вылегжанин И.А., Пожидаев А.В., Остроменский П.И., Шандаров Л.Г., 2014
Предисловие
Опыт использования части I практикума в 2011/12 учеб. г. при обучении студентов первого курса инженерных специальностей СГУПСа показал, что принятая форма изложения учебного материала является достаточно удачной и эффективной.
Учебный материал разбит на отдельные, по возможности замкнутые, темы. Каждая тема содержит:
–краткий теоретический материал, необходимый для решения типовых задач по теме;
–подробное изложение методик решения разных видов типовых задач;
–задачи в количестве, достаточном для проведения аудиторных занятий (2–3 ч в неделю) и самостоятельного решения (с ответами);
–прикладные задачи, которые с помощью методов математического моделирования приводятся к математическим задачам, методики решения которых изучаются в теме;
–образцы решенных задач с текстовыми пояснениями;
–подробный перечень конкретных требований к практическому усвоению студентом каждой темы.
Указанный перечень позволяет студенту и преподавателю, ведущему практические занятия, однозначно понимать, что должен знать и уметь студент после изучения темы. Кроме того, компактное представление знаний и умений в виде перечня дает возможность преподавателям других кафедр быстро оценить уро-
3
вень компетентности, который будет иметь студент при успешном изучении темы.
Объем учебных материалов, приведенный в части II практикума, соответствует государственным образовательным стандартам третьего поколения для специалистов, изучающих дисциплину общим объемом 570–650 учеб. ч, и бакалавров, которым на овладение дисциплиной выделяется 360–440 учеб. ч, по инже- нерно-техническим направлениям подготовки в области строительства и эксплуатации железных и автомобильных дорог, транспортных мостов и тоннелей, разработки и эксплуатации подъем- но-транспортных и технологических машин и оборудования.
При самостоятельном решении задач необходимо приводить краткие пояснения, которые:
–повышают понимание и усвоение логической последовательности шагов решения задач;
–позволяют сформировать оценочные суждения при выборе наиболее рационального варианта решения из нескольких возможных;
–способствуют выработке навыка перенесения изучаемого алгоритма решения на аналогичные задачи практикума и далее на похожие расчетные ситуации в инженерной деятельности.
При изучении математического анализа особое внимание необходимо уделять геометрической и прикладным интерпретациям аналитических вычислений. Эффективные приложения математики в инженерной деятельности в значительной степени связаны с удачными интерпретациями.
4
Введение
Математический анализ – часть математики, в которой изучаются методы исследования функций и операции с математическими объектами, содержащими функции, на основе предельных переходов (пределов).
Физические явления, законы движения и процессы взаимодействия в технических системах обычно описываются с помощью функций и математических объектов, содержащих функции. Поэтому хорошее знание основ математического анализа является важнейшей частью математического образования инженера. Эти знания, безусловно, необходимы для осознанного качественного усвоения общетехнических и специальных учебных дисциплин, а также успешного использования в инженерной деятельности при математическом моделировании технических и производственных систем.
В общем случае числовая функция – математический объект, характеризующий однозначное соответствие между элементами двух числовых множеств.
Общее обозначение функции – f : X Y , где числовое множество Х – область существования (область определения)
функции; числовое множество Y – область значений функции;
f– условное обозначение (знак) функции.
Вкурсах высшей математики, ориентированных на инженерные, экономические и другие приложения, любой элемент из множества Х обычно называют независимой переменной (аргу-
ментом). Любой элемент из области значений функции называ-
ется зависимой переменной величиной, или значением функции.
Функциональную зависимость между указанными переменными
выражают в виде: y f x , y f x1,x2, ,xn и т.п.
Функции классифицируют по разным критериям. В частности, класс функций действительных переменных, аргументами которых являются действительные числа, можно разбить на четыре существенно различных класса:
5
1)скалярные функции одной переменной y = f(x), у которых аргументом являются скалярные величины (дискретные или непрерывные);
2)векторные функции одного скалярного аргумента: r r(t), где t R;
3)скалярные функции нескольких скалярных аргументов или
одного векторного аргумента: y y(x1,x2, ,xn ) либо y y(r),
где r x1,x2, ,xn , x1,x2, ,xn Rn;
4) векторные функции одного векторного аргумента:
rf .
Вчасти II практикума будем рассматривать скалярные функции одной действительной переменной и математические объекты, существенно связанные с этими функциями, а также векторные функции одного скалярного аргумента. Функции нескольких переменных и их приложения изучаются в части III практикума.
Тема 5: Числовые последовательности
иих пределы
5.1.Исходные положения
Числовой последовательностью называется дискретная функция fn : N R, описывающая соответствие между числами из множества натуральных чисел n N и числами из множества действительных чисел y R.
В развернутом виде числовую последовательность представляют так: y1, y2, , yn, yn ; yn – общие члены последова-
тельности, которые, как правило, представляются в виде формул, позволяющих определить любой член последовательности по его номеру (или по значениям одного или нескольких предыдущих членов); yn , vn , an – условные обозначения последователь-
ности в целом.
Примеры:
1) |
1 |
2 |
3 |
4 |
|
n |
|
n |
|
; |
||||
|
, |
|
, |
|
, |
|
, , |
|
|
, |
|
|
||
|
|
|
|
n 1 |
|
|||||||||
|
2 3 4 5 |
|
n 1 |
|
||||||||||
6

2)1, 1,1, 1,1, , 1 n 1, 1 n 1 ;
3)десятичные приближения числа 
 2: 1,4; 1,41; 1,414; 1,4142; … .
2: 1,4; 1,41; 1,414; 1,4142; … .
Общий член последовательности может быть представлен рекуррентной формулой, позволяющей определить последующий член, если известны один или несколько предыдущих членов.
Из школьной математики известны два вида последовательностей: арифметические и геометрические прогрессии. Члены арифметической прогрессии можно определить с помощью общей формулы
an a1 n 1 d ,
где а1 – первый член последовательности; d – разность прогрессии. Их можно также определить с помощью рекуррентной формулы an an 1 d, позволяющей находить каждый последующий член по предыдущему. Аналогичные формулы имеют место и для геометрической прогрессии:
bn b1qn 1,
где b1 – первый член геометрической прогрессии; q – ее знаменатель (общая формула); bn bn 1q – рекуррентная формула.
В приложениях важную роль играют монотонные и ограниченные последовательности.
Монотонными называются возрастающие y1 y2 ... yn ...
и убывающие y1 y2 ... yn ... последовательности.
|
|
|
Последовательность yn называется ограниченной, если все |
|||
ее |
|
члены |
находятся |
в ограниченном числовом |
интервале |
|
M; M , |
т.е. для любого члена последовательности yn имеем |
|||||
|
yn |
|
M . При необходимости различают последовательности, ог- |
|||
|
|
|||||
|
раниченные сверху yn |
M и ограниченные снизу yn |
M . |
|||
Примеры:
1) |
1 |
, |
2 |
, |
3 |
, |
4 |
, , |
n |
, – ограниченная |
M 1 моно- |
|
3 |
|
|
|
|||||||
2 |
|
|
4 5 |
|
n 1 |
|
|||||
тонно возрастающая последовательность;
7
2)1, 2, 3, 4, 5, … – ограниченная снизу, но не ограниченная сверху монотонно возрастающая последовательность;
3)1, –1, 1, –1, 1, …, (–1)n+1, … – ограниченная M 1 немо-
нотонная последовательность;
4) 1, –2, 3, –4, 5, …, (–1)n+1n, … – неограниченная немонотон-
ная последовательность.
Задачи к разделу 5.1
5.1.1. Для следующих последовательностей определить пять их первых членов:
а) a |
|
1 |
; б) b |
1 |
; в) c |
|
|
n 3 |
; г) d |
|
2n |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||
|
n |
|
|
n2 |
|
|
n |
|
2n |
|
n |
|
n2 1 |
|
n |
n! |
||||
д) sn |
|
2n |
1 n 2n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.1.2. Для следующих последовательностей выписать по пять их первых членов:
а) f |
1 |
1; |
f |
n |
3 f |
n 1 |
; б) b |
1 |
; |
b |
bn 1 |
; |
|
|
|
|||
2 |
2 |
|
||||||||||||||||
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
в) v1 1; |
vn |
|
|
|
; г) w1 1; |
wn 1 |
|
. |
||||||||||
1 vn 1 |
wn 1 |
|||||||||||||||||
Убедиться, что последовательность б данной задачи совпадает с последовательностью б предыдущей задачи.
5.1.3. Для следующих последовательностей выписать по пять членов, начиная с третьего:
а) f1 = 1; f2 = 1; fn = fn–1 + fn–2 (числа Фибоначчи);
б) g1 1; g2 1;gn 2gn 1 3gn 2 .
5.1.4. Проверить, является ли последовательность монотонной и ограниченной:
а) an |
|
1 |
; б) cn |
|
n 3 |
; в) dn |
|
2n |
; г) sn |
|
2n 1 n 2n |
. |
||
n2 |
|
|
|
|
|
|||||||||
|
|
|
|
n2 1 |
|
n! |
|
|
n |
|||||
5.1.5. Доказать, что последовательность монотонна и ограничена:
1
а) t1 1; tn tn 1 2n ; б)u1  2; un
2; un  2 un 1 .
2 un 1 .
8

5.2. Предел числовой последовательности. Геометрическое представление предела последовательности
Число A называется пределом числовой последовательности
yn , если при неограниченном увеличении числа n (n ) для любого заранее выбранного как угодно малого числа 0 найдется такой член последовательности с номером n , что все по-
следующие члены последовательности с номерами n n будут находиться внутри интервала
|
|
A yn A . |
(5.1) |
||||
Из (5.1) следует, что |
|
||||||
|
|
yn A |
|
при n n . |
(5.2) |
||
|
|
|
|||||
Условные обозначения: lim yn A или yn A при n . |
|||||||
|
|
n |
|
||||
Используя определение предела, можно проверить, является |
|||||||
ли известное число А пределом данной последовательности. |
|
||||||
Пример. Проверить, является ли число A 1 пределом |
|||||||
последовательности yn |
1 |
1 n |
. |
|
|||
|
|
||||||
Решение. Пусть |
|
|
|
|
n |
|
|
задано некоторое число 0. |
Если |
||||||
lim yn 1, то должно по определению выполняться неравенство |
|||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
yn 1 |
|
|
|
|
1 n |
1 |
|
|
|
|
|
1 n |
|
|
1 |
|
||||||||||
|
|
, т.е. |
1 |
|
|
|
. |
||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
n |
|||
Из неравенства |
|
получаем n |
– формулу, позволяю- |
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
щую находить n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в зависимости от заданного (любого) числа . |
|||||||||||||||||||||||||||
В качестве n можно, например, |
взять любое целое число |
||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|||||||||||
больше чем |
|
, в частности число |
|
|
|
1, где |
|
|
|
– целая часть |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(антье) числа 1.
1
Проверка. Пусть 0,2, тогда n 0,2 1 6.
0,2
9
|
При n 4 получим |
|
1 |
1 4 |
1 |
|
|
1 4 |
|
1 |
0,25 0,2, при |
||||||||
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
4 |
|
|
|
4 |
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
n2 |
6 получим |
|
1 6 |
1 |
|
|
1 |
|
0,167 0,2. Таким образом, при |
||||||||||
1 |
|
|
|||||||||||||||||
|
|
||||||||||||||||||
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|||||
n 5 все члены последовательности будут находиться внутри ин-
тервала 0,8 yn 1,2. |
|
|
|
|
|
|
|
|
|
||||||
|
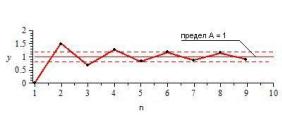
Для наглядного представления предела составим для после- |
||||||||||||||
довательности yn 1 |
1 n |
|
таблицу и по ней построим график |
||||||||||||
|
n |
||||||||||||||
(рис. 5.1). |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
1 |
|
2 |
3 |
4 |
|
5 |
|
6 |
7 |
8 |
9 |
10 |
… |
yn |
|
0 |
|
1,5 |
0,67 |
1,25 |
|
0,8 |
|
1,17 |
0,86 |
1,14 |
0,89 |
1,1 |
… |
Рис. 5.1. Графическое изображение предела последовательности
Из таблицы и рис. 5.1 следует, что при n график функции (последовательности) стремится к прямой линии y A 1,
которая соответствует пределу последовательности.
Интервал A , A называется -окрестностью пре-
дельной точки A (числа A).
Замечание. Общее математическое определение предельной точки несколько шире, но оно нам пока не понадобится.
Числовая последовательность yn имеет предел, равный бес-
конечности (или плюс бесконечности) (lim yn ), если при
n
n для любого заранее выбранного как угодно большого числа E 0 найдется такой член последовательности с номером
10
