
m0936
.pdf
ми. В математике по умолчанию рассматривают значения функций, соответствующие наименьшему (главному) периоду:
|
|
|
|
|
|
y cosx при x 0; ; |
|||||
y sinx при x |
|
|
|
; |
|
|
|
; |
|||
2 |
|
|
|||||||||
|
|
|
2 |
|
|
|
|||||
|
|
|
|
y ctgx при x 0; ; |
|||||||
y tgx при x |
|
; |
|
|
; |
||||||
2 |
|
|
|||||||||
|
|
|
2 |
|
|
|
|||||
– обратные тригонометрические |
функции: |
y arcsinx при |
|||||||||
x 1;1 ; y arccosx |
при x 1;1 ; |
y arctg x |
при x ; ; |
||||||||
y arcctgx при x ; . В общем случае обратные тригоно-
метрические функции являются многозначными. В указанных выше областях определения тригонометрических функций (являющихся областями значений для обратных тригонометрических функций) выполняются условия однозначности.
Графики основных элементарных функций представлены в прил. А.
Из основных элементарных функций образуют другие элементарные функции (составные и сложные).
Составные элементарные функции образуются из основных элементарных функций с помощью конечного числа арифметических операций и могут быть представлены одной аналитической формулой в области существования функции.
Пример. y 2lnx 6 – элементарная функция, составлен-
3 x2
x2
ная из основных элементарных функций с помощью арифметических операций.
Другим важным способом составления элементарных функций является композиция (суперпозиция) элементарных функций. В результате образуется сложная элементарная функция.
Если аргументом элементарной функции является тоже элементарная функция, то такая функция от функции называется
сложной.
Сложную функцию можно разложить на основные элементарные функции с промежуточными аргументами.
31

Пример. y sin2 
 x [u
x [u 
 x, v sinu, y v2 ]; y v2 y sinu 2 sin2 u y sin2
x, v sinu, y v2 ]; y v2 y sinu 2 sin2 u y sin2 
 x,
x,
где u и v – промежуточные аргументы; x – основной аргумент; функции v v u , y y v – основные элементарные функции
промежуточных аргументов.
При составлении сложной функции важен порядок следования функций в ее композиции.
Пример. Если f x x3, а g x sinx, то g f x sinx3, а f g x sin3 x. Получили принципиально различные по свойствам функции. В частности, первая из этих функций не является периодической, а вторая является.
Замечание. При составлении элементарных функций можно одновременно использовать операцию композиции и арифметические операции.
|
y |
|
3x |
|
|
|
|
|
|
1 |
|
|
x 1 2 |
|
|
|
|
|
|
|
|
|
|
||||||||
Например, |
sin |
|
|
; |
y |
|
|
|
|
e |
2 . |
||||
7 |
|
|
|||||||||||||
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
Если функцию нельзя представить в виде одного аналитического выражения (формулы), содержащего элементарные функции, объединенные конечным числом арифметических операций и (или) посредством композиции, то такую функцию называют
неэлементарной.
Примеры. Простейшие неэлементарные функции:
1 при x 0,
1) y sgn x 0 при x 0,
1 при x 0 (читается «сигнум икс», рис. 6.1); 2) единичная функция Хевисайда
0 при x 0, y x
1 при x 0
(рис. 6.2).
32
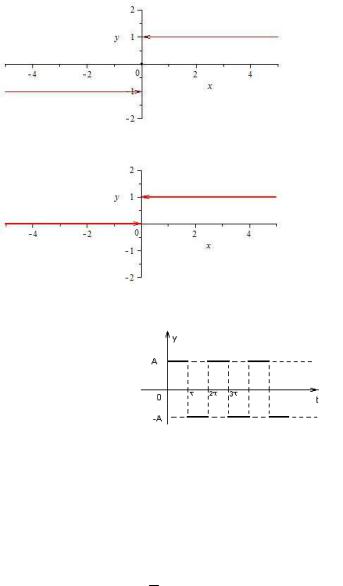
Рис. 6.1. График функции «сигнум х»
Рис. 6.2. График функции Хевисайда
С помощью арифметических операций из простейших неэлементарных функций образуют составные неэлементарные функции.
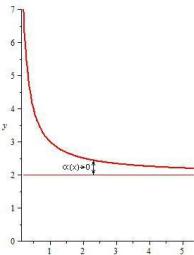
Пример. Периодически повторяющийся прямоугольный импульс (рис. 6.3):
Рис. 6.3. Периодический прямоугольный импульс
yA t 2 t 2 t 2 ... .
Внастоящее время неэлементарные функции широко используются в теории автоматического управления, радиоэлектронике и вычислительной технике.
Задачи к разделу 6.2
6.2.1. Даны функции: f x 
 x; g x arcsinx; h x 3x .
x; g x arcsinx; h x 3x .
Найти функции: f g h x , f h g x , f f h x ,
f f f x , |
f f g x , |
f g f x , |
f g g x , |
f h f x , |
f h h x , |
g f f x , |
g f g x , |
g f h x , |
g g f x , |
|
|
|
|
33 |

g g g x , |
g g h x , |
g h f x , |
g h g x , |
g h h x , |
h f f x , |
h f g x , |
h f h x , |
h g f x , |
h g g x , |
h g h x , |
h h f x , |
h h g x , |
h h h x . |
|
6.2.2. Найти f x , если: |
|
|
||
а) f x 1 x2 5x 6; б) f x2 x2 5x 6; |
|
|||
в) f 2x x2 5x 6; г) |
f lnx x2 5x 6. |
|
||
6.2.3. Показать, что следующие функции являются элементарными:
а) |
|
|
2x, |
если |
x 0, |
б) |
|
|
x |
|
, |
если |
x 0, |
||
y |
|
2x |
|
, |
если |
x 0; |
y |
|
|
|
|
если |
x 0. |
||
|
|
|
|
||||||||||||
|
|
||||||||||||||
|
|
|
|
|
eln x, |
||||||||||
6.2.4. Построить графики функций:
а) y x 3 2 4; б) y x 5 3; в) y 
 x 2 3; г)y
x 2 3; г)y 
 x ;
x ;
д)y |
|
; е)y |
1 |
2; ж)y |
1 |
; з) y |
x 1 |
. |
|
1 x |
|||||||||
|
x 2 |
|
|||||||
|
|
|
x |
|
x 2 |
||||
6.2.5. Построить графики функций:
а) y 2x 1; б)y 2x 1; в) y log2 x 1 ; г)y log2 x 1.
6.2.6. Построить графики функций:
а) y |
|
2 и y |
x2 |
; б) y lnex и y eln x ; |
x |
в) y sin arcsinx и y arcsin sinx .
6.2.7. Построить графики функций:
а) y x – целая часть х; б) y x – дробная часть х;
в) y x – число простых чисел, не превышающих числа х при x 0, 20 .
6.2.8. Убедиться в том, что график функции Дирихле
0 при x Q, y
1 при x Q не существует в его обычном понимании.
6.3. Пределы функций в точке и на бесконечности
Для функций одной действительной переменной вводят два вида пределов:
–предел функции на бесконечности (или на минус бесконечности);
–предел функции в точке.
34

Пусть дана функция y f x и x , или x a, .
Число A называется пределом функции y f x на бесконеч-
ности, если для любого сколь угодно малого числа 0 найдется такое значение аргумента x , после которого при всех значе-
ниях аргумента x x значения функции будут находиться внутри интервала A , A .
Условие попадания в интервал A , A равносильно не-
равенству f x A .
Символьная запись предела функции на бесконечности имеет
вид: lim f x A или f x A при x .
x
При введении понятия предела функции в точке используют понятия -окрестности точки (числа) и предельной точки (числа).
Любой интервал числовой оси, содержащий точку x a, на-
зывается окрестностью этой точки. Интервал a , a на-
зывается |
-окрестностью |
точки |
x a. |
Множество |
|
a , a a, a |
называется проколотой -окрестностью |
||||
точки x a. Если предельная точка |
|
|
|||
x a принадлежит своей -окрест- |
|
|
|||
ности, то эту окрестность называют |
|
|
|||
полной. |
Условные |
графические |
|
|
|
изображения -окрестностей показаны на рис. 6.4.
Точка a называется предельной точкой числового множества М,
если в любой как угодно малой окрестности точки a содержатся числа из множества М.
Пример. Пусть множество M является интервалом ,
на числовой оси. Предельными точками этого множества являются все точки интервала , , а также концы этого интервала и
. Других предельных точек у множества M нет. |
|
|||||
Число A называется |
пределом |
функции y f x |
в точке |
|||
x a, если для любого как угодно |
малого числа 0 найдется |
|||||
такое |
число |
, |
что |
для |
любого |
значения |
35

x a , |
a a, |
a все значения функции f x будут нахо- |
диться внутри интервала A , A .
Символьная запись предела функции в точке: lim f x A.
x a
Замечание 1. Из определения предела функции в точке следует, что функция должна быть определена в некоторой проколотой -окрестности предельной точки x = a, но не обязательно в самой точке.
Замечание 2. В данном разделе использована геометрическая интерпретация действительных чисел в виде точек на числовой оси. Если рассматривается некоторое множество действительных чисел E, то при геометрической интерпретации различают:
–внутренние точки множества E, если они входят вместе с некоторой окрестностью в это множество;
–граничные точки множества E, для каждой из которых ее окрестность содержит точки, принадлежащие и не принадлежащие множеству E.
Задачи к разделу 6.3
6.3.1. Сформулировать определение предела функции y f x на минус бесконечности и дать его геометрическую ин-
терпретацию.
6.3.2.Найти все предельные точки множеств:
а) a, b b, c ; б) a; b .
6.3.3.Провести аналогию между пределом последовательности и пределом функции на бесконечности и вычислить следующие пределы:
а) |
lim |
4x 1 |
|
; б) lim |
|
|
|
|
|
; |
||||||
|
|
x 1 |
x |
|||||||||||||
|
|
|||||||||||||||
|
x 2 5x |
|
|
|
x |
|
|
|
|
|
|
|
||||
|
x 2 |
|
|
x |
|
sin2x |
|
|
|
|||||||
в) |
lim |
|
|
|
|
; г) lim |
|
|
|
|
. |
|
|
|||
|
|
|
|
|
x |
|
|
|||||||||
|
x 2x 1 |
|
x 0 |
|
|
|
|
|||||||||
6.3.4.Дать определение того, что число A не является пределом функции y f x при x a.
6.3.5.Дать определение того, что никакое число не является пределом функции y f x : а) при x a; б) при x .
36

6.4.Основные свойства пределов функций в точке
ина бесконечности
Основные свойства пределов функций с непрерывным аргументом совпадают с аналогичными свойствами числовых последовательностей.
1.Если предел функции существует, то он единственный.
2.Предел постоянной величины равен этой постоянной:
limC C (limC C).
|
|
|
|
|
|
|
|
x a |
x a |
|
|
|
|
|
|
|
|
|||
3. Если существуют конечные пределы |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
lim f x A и limg x B, |
|
|
|||||||||||
|
|
|
|
|
|
|
x a |
x a |
|
|
|
|
|
|
|
|||||
то: |
lim f x g x A B; |
|
|
|
|
|
|
|
|
|
|
|
||||||||
а) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
lim f x g x AB; |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
lim |
f x |
|
|
A |
, если B 0; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x a g x |
B |
|
|
|
|
|
|
|
|
|
|
|
|||||||
г) |
limCf x Clim f x CA; |
|
|
|
|
|
|
|
|
|
||||||||||
|
x a |
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
||||
д) |
limk |
|
k |
|
k |
|
, |
если |
k |
|
|
имеет смысл во |
||||||||
f x |
lim f x |
A |
A |
|||||||||||||||||
|
x a |
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|||
множестве действительных чисел; |
|
|
|
|
|
|
|
|
|
|||||||||||
е) |
lim f x k |
(lim f (х) k Ak , если Ak |
имеет смысл во мно- |
|||||||||||||||||
|
x a |
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
||||
жестве действительных чисел; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ж) |
limln f x lnlim f x ln A, |
если |
ln A |
имеет смысл во |
||||||||||||||||
|
x a |
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|||
множестве действительных чисел; |
|
|
|
|
|
|
|
|
|
|||||||||||
з) |
lim f x |
g x |
|
|
|
lim g x |
|
A |
B |
, если A |
B |
имеет смысл во |
||||||||
|
|
(lim f (х) x a |
|
|
|
|
||||||||||||||
|
x a |
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
||||
множестве действительных чисел.
Эти равенства остаются верными, если вместо пределов при x a рассматривать пределы при x или x .
37
6.5. Бесконечно малые функции и их свойства
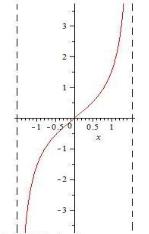
Функция y x называет-
ся бесконечно малой (б.м.ф.) при
x a (или |
при x ), если |
lim x 0 |
(соответственно |
x a |
|
lim x 0), рис. 6.5.
x
Если функция y f x име-
ет конечный предел A, то в окрестности предельного значения имеет место равенство f x A x .
|
Пример. |
Найти предел |
|||
функции f x |
2x 1 |
. |
|||
|
|
||||
|
Решение. |
x |
|||
|
|
|
|
||
lim f x lim |
2x 1 |
|
|||
|
|||||
x |
x |
x |
|||
Рис. 6.5. Бесконечно малая функция
|
|
1 |
|
1 |
|
1 |
|
|
lim |
2 |
|
|
2 lim |
|
; |
|
– бесконечно малая функция при |
x |
|
x |
||||||
x |
|
|
x x |
|
||||
x .
Замечание 1. В прикладных задачах бесконечно малые постоянные величины (например, масса электрона, размеры атома и т.п.) с математической точки зрения не являются бесконечно малыми. Эти величины постоянны и не стремятся в пределе к нулю. В математике бесконечно малые величины являются функциями.
Замечание 2. Понятие бесконечной малости существенно зависит от того, к чему стремится аргумент. Функция, являющаяся бесконечно малой при x a, может не быть таковой, например, при x b a.
Свойства бесконечно малых последовательностей (б.м.п.) дословно переносятся на бесконечно малые функции:
1)сумма конечного количества б.м.ф. является б.м.ф.;
2)произведение конечного количества б.м.ф. является б.м.ф.;
38
3)произведение ограниченной функции и б.м.ф. является б.м.ф.;
4)произведение любого числа и б.м.ф. остается б.м.ф.
В приложениях наиболее часто встречаются пределы б.м.ф.
следующих видов: lim |
1 |
0 при p 0; limqx |
0 при |
|
q |
|
1. |
||
|
|
||||||||
|
|||||||||
x xp |
x |
|
|
|
|
|
|||
|
|
|
|
|
|||||
6.6. Бесконечно большие функции и их свойства |
|||||||||
Функция y x называется |
бесконечно |
большой (б.б.ф.) |
|||||||
при x a (или при x ), если lim x (соответственно
x a
lim x ).
x
Одна и та же функция может быть бесконечно малой и бесконечно большой в различных частях области существования.
|
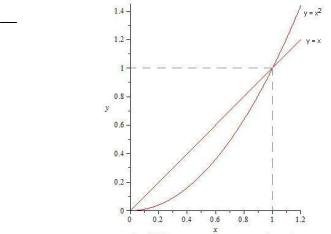
Пример. Функция |
y tgx, |
|||||||||||||
определенная |
в |
|
интервале |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
, |
|
|
|
|
, |
является |
б.б.ф. |
при |
|||||
2 |
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
x |
|
|
и |
при |
x |
|
. |
Эта |
же |
||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
функция является б.м.ф. при x 0 |
|||||||||||||||
(рис. 6.6). |
|
|
|
|
|
|
|
||||||||
|
Бесконечно большие и беско- |
||||||||||||||
нечно малые функции взаимосвя- |
|||||||||||||||
заны между собой. Если |
x – |
||||||||||||||
б.б.ф., |
то функция x |
1 |
|
яв- |
|||||||||||
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ляется б.м.ф. |
Рис. 6.6. Функция y = tg x |
|
6.7. Сравнение функций. Эквивалентная замена функций
При сравнении двух функций x и x , каждую из кото-
рых при x a (или при x ) можно считать бесконечно малой величиной, возможны три случая.
39
1. lim |
x |
|
0 или |
lim |
x |
|
0. В этом случае |
x называет- |
x a x |
|
x x |
|
|
||||
ся бесконечно малой величиной более высокого порядка, чемx . Пишут: x x или x o x . Знак o читается
«о малое».
Пример. lim x2 limx 0,
x 0 x x 0
значит, в окрестности нуля функ-
ция y x2 является бесконечно малой функцией более высокого порядка, чем y x (рис. 6.7).
|
2. Если |
lim |
x |
|
1 |
или |
|||
|
|
||||||||
|
x |
|
|
x a x |
|
|
|||
lim |
|
1, |
то эти |
бесконечно |
|||||
|
|||||||||
x x |
|
|
|
|
|
|
|||
малые функции называются экви-
валентными. Пишут: x ~ x .
|
Пример. Функции sinx |
и Рис. 6.7. Сравнение порядков малости |
|||||||||
tgx эквивалентны при x 0: |
|
|
|
функций |
|
||||||
|
|
|
|
|
|||||||
lim |
sinx |
limcosx 1 (рис. 6.8). |
|
|
|||||||
|
|
|
|||||||||
x 0 tgx |
|
x 0 |
|
|
|
|
|
||||
|
3. Если |
lim |
x |
K или |
lim |
x |
K, где |
K R, |
K 0, |
||
|
|
|
|||||||||
|
|
|
|
x a x |
x x |
|
|
||||
K 1, |
x |
и x – бесконечно малые функции, имеющие ко- |
|||||||||
нечный порядок малости друг относительно друга. В этом случае условие эквивалентности имеет вид x ~K x .
40
