
m0936
.pdf
График не имеет наклонных и горизонтальных асимптот.
Изображаем эскиз графика функции по результатам первого этапа (рис. 10.6):
–функция общего вида не имеет точек разрыва и асимптот;
–нули функции имеют место
при x 0 и x 1;
|
– в интервалах ,0 и |
0,1 |
Рис. 10.6. Эскиз графика функции |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y x 3 |
|
x2 |
|
|
||||||||||||||||||||||||
функция отрицательна, в интер- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
вале 1, – положительна; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
– в пробной точке x 1 значение функции y 1 2. |
||||||||||||||||||||||||||||||||||||
|
2. Исследование свойств функции с использованием произ- |
||||||||||||||||||||||||||||||||||||
водных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2.1. Находим критические точки первого рода: |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
y x 3 |
|
x2 1 |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
При |
производная |
|
|
|
|
не существует (правая произ- |
||||||||||||||||||||||||||||||
|
y 0 |
||||||||||||||||||||||||||||||||||||
водная равна , а левая – равна ). При |
1 |
|
2 |
|
|
0 получим |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
3 3 x |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
8 |
|
|
8 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
, y |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
27 |
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Имеется две критические точки первого рода, |
из которых |
|||||||||||||||||||||||||||||||||||
первая x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
||||||||||
является особой точкой, |
а вторая x |
|
|
– ста- |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|||||
ционарной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2.2. Находим критические точки второго рода: |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
1 |
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
3 |
|
|
|
|
0, |
|
||||||||||||||
|
|
|
|
3 3 |
|
|
3 |
3 |
9x3 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||
поэтому имеется одна критическая точка второго рода x 0. 2.3. Составляем сводную таблицу результатов, необходимых
для построения графика (табл. 10.3).
161

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 10.3 |
||
|
|
|
|
|
|
|
|
Характеристика поведения функции y x 3 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знак или |
|
Знак первой |
Знак второй |
|
|
|
||||||||||
Характерные |
|
числовое |
|
|
|
|
||||||||||||||||||||
|
|
производной |
производной |
Краткая характеристи- |
||||||||||||||||||||||
точки (х) и |
значение |
|
функции |
функции |
ка поведения функции |
|||||||||||||||||||||
интервалы |
|
|
функции |
|
|
f (х) |
f (х) |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
,0 |
|
|
|
– |
|
|
|
|
|
|
|
|
|
+ |
+ |
Возрастает, выпукла |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вниз |
||
|
|
х = 0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
Не сущест- |
Не сущест- |
Нуль функции, крити- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вует |
вует |
ческая точка первого |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рода – максимум, кри- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тическая точка второго |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рода – перегиба нет |
||
|
0, |
|
|
8 |
|
|
|
– |
|
|
|
|
|
|
|
|
|
– |
+ |
Убывает, выпукла вниз |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
8 |
|
|
|
|
4 |
|
|
|
|
|
|
|
0 |
+ |
Критическая точка |
||||||||||
|
|
|
|
27 |
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
первого рода – мини- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мум |
||
8 |
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
+ |
+ |
Возрастает, выпукла |
|||||||
|
|
|
|
|
,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вниз |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
х = 1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Нуль функции |
||||||||
|
1, |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
+ |
Возрастает, выпукла |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вниз |
||
|
|
2.4. Определяем характер монотонности и выпуклости в ин- |
||||||||||||||||||||||||
тервалах, приведенных в сводной таблице. |
|
|
|
|||||||||||||||||||||||
|
|
Интервал ,0 : xпр |
1; |
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
0, функция возрастает; |
|||||||||||||||
|
|
33 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
y |
1 |
|
1 |
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0, функция выпукла вниз. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
y |
|
1 |
9 1 3 1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0, |
|
8 |
: x |
0,1; |
|
|
|
|
|||||||
|
|
Интервал |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
пр |
|
|
|
|
|
||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
0, функция убывает; |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
y |
0,1 |
33 |
0,1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
162

2
y 0,1 0, функция выпукла вниз. 9 0,13 0,1
Интервал |
|
8 |
|
|
|
|
: x |
|
0,5; |
||||||
|
|
|
|
|
,1 |
|
|||||||||
27 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
пр |
|
||||
|
|
|
|
2 |
|
0, функция возрастает; |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
y 0,5 1 |
33 |
|
|
0,5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
0, функция выпукла вниз. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
y 0,5 |
|
0,53 0,5 |
|
||||||||||||
|
|
9 |
|
|
|
|
|||||||||
Интервал 1, : xпр |
|
2; |
|||||||||||||
|
|
|
|
2 |
|
|
|
0, функция возрастает; |
|||||||
|
|
|
|
|
|
|
|
||||||||
y 2 1 |
3 |
3 2 |
|
||||||||||||
|
|
|
2 |
|
|
|
|
0, функция выпукла вниз. |
|||||||
|
|
|
|
|
|
|
|
||||||||
y 2 |
9 23 2 |
||||||||||||||
2.5. Определяем возможные экстремумы в критических точках первого рода. В особой точке x 0 возможен «острый» экстремум. Проверим это, используя первое достаточное условие наличия экстремума:
xпр |
|
|
1 0, y 1 0 |
||
|
|
в точке x 0 – максимум. |
xпр |
0,1 0, |
|
y 0,1 0 |
||
Критическая точка первого рода x 8 является точкой ста27
ционарности. Используем первый способ определения экстремума:
|
|
8 |
|
|
xпр |
0,1 |
|
, |
|
27 |
y 0,1 0 |
|||
|
|
|
в точке x 0 – минимум. |
|
xпр |
0,5 |
8 |
, |
y 0,5 0 |
|
27
В точке x 8 функция гладкая, поэтому для проверки ис27
пользуем второе достаточное условие наличия экстремума.
8 |
|
|
8 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Проверка. При x |
имеем |
|
|
|
|
|
|
|
0 – ми- |
||
|
|
|
|
|
|
||||||
y |
27 |
|
|
|
|
|
|||||
27 |
|
|
|
9 |
8 |
3 |
|
8 |
|
||
|
|
|
|
|
|
|
27 |
|
|||
|
|
|
|
|
|
27 |
|
|
|
||
нимум.
163

2.6. Определяем, является ли критическая точка второго рода точкой перегиба.
xпр |
|
|
1 0, y 1 0 |
||
|
|
в точке x 0 перегиба нет. |
xпр |
0,1 0, |
|
y 0,1 0 |
||
2.7. По данным сводной таблицы и эскизу графика функции строим график (рис. 10.7).
Рис. 10.7. График функции y x 3 x2
x2
10.5.Пример полного исследования разрывной функции
ипостроение графика
Дана функция y f x |
x3 |
. Требуется провести полное |
|
x 1 2 |
|||
|
|
исследование функции и построить ее график.
1. Исследование без использования производных.
1.1. Анализируем общие свойства функции (непрерывность, симметричность, периодичность).
Функция определена на всей числовой прямой за исключени-
ем точки |
x 1, являющейся точкой разрыва второго рода |
y 1 . |
Область естественного существования функции со- |
стоит из двух интервалов непрерывности D f ,1 1, .
Функция несимметрична относительно оси Oy и начала ко-
x3
ординат, так как f x x 1 2 x 1 2 f x .
164

Функция не является периодической (это следует, например,
из того, что lim |
x3 |
, т.е. поведение функции на бесконеч- |
|
||
x x 1 2 |
|
|
ности не повторяется).
Таким образом, имеем функцию общего вида с одной точкой разрыва. Из-за общего характера функции ее необходимо исследовать во всех точках интервалов непрерывности.
1.2. Находим координаты точек пересечения графика функции с осями координат. Сначала определяем нули функции из
x3
уравнения x 1 2 0 y 0 при x 0. Ось Oy функция пересе-
кает при x 0, точка x 0 является нулем функции.
1.3. Определяем интервалы знакопостоянства функции. Интервал непрерывности ,1 делится нулем функции x 0 на два интервала знакопостоянства , 0 и 0,1 . Интервал знако-
постоянства 1, совпадает с интервалом непрерывности. Опре-
делим знаки функции в указанных интервалах.
1 3 1
Интервал , 0 : xпр 1; y 1 1 1 2 4 0.
0,5 3 1 Интервал 0,1 : xпр 0,5; y 0,5 0,5 1 2 2 0.
2 3
Интервал 1, : xпр 2; y 2 2 1 2 8 0.
1.4. Определяем асимптотическое поведение функции в окрестности точки разрыва второго рода с помощью односторонних пределов:
lim |
x3 |
, lim |
|
x3 |
. |
|
x 1 2 |
x 1 2 |
|||||
x 1 0 |
x 1 0 |
|
||||
В окрестности точки разрыва x 1 |
функция стремится к |
|||||
слева и справа. Значит, имеется вертикальная асимптота с уравнением x 1.
Проверим наличие наклонной асимптоты y kx b:
165
k lim |
f x |
|
|
x3 |
|
|
|
|
|
1 |
|
1; |
|
|||
|
lim |
|
|
|
|
lim |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
2 |
|
||||||
x |
x |
x x x 1 2 |
x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b lim f x kx lim |
|
x3 |
|
|
|
x3 |
x3 2x2 x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 x |
lim |
|
|
|
2 |
2. |
|||||||||
|
|
|
|
|
|
|||||||||||
x |
x |
x 1 |
|
x |
|
x 1 |
|
|||||||||
Таким образом, как при x , так и при x имеет место наклонная асимптота y x 2. Определим характер прибли-
жения к асимптоте графика функции.
|
|
|
|
|
|
x3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
lim f x kx b lim |
|
x 2 |
|
|
||||||||||
|
x |
|
|
|
x x 1 |
|
|
|
|
|
|||||
|
|
lim |
3x 1 |
lim |
|
|
3 |
|
0. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x x 1 2 |
x 2 x 1 |
|
|
|
|
|
|||||||
При x |
график функции лежит выше наклонной асим- |
||||||||||||||
птоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|||||||
|
lim f x kx b lim |
x 2 |
|
|
|||||||||||
|
x |
|
|
|
x |
x 1 |
|
|
|
|
|
||||
|
|
lim |
3x 1 |
lim |
|
3 |
|
|
|
0. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x x 1 2 |
x 2 x 1 |
|
|
|
|||||||||
При x |
график функции лежит ниже наклонной асим- |
||||||||||||||
птоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
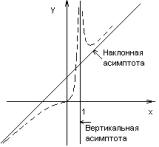
1.5. Изображаем |
эскиз |
графика |
|
|
|
|
|
||||||||
функции по результатам первого этапа |
|
|
|
|
|
||||||||||
исследования (рис. 10.8): |
|
|
|
|
|
|
|
|
|
|
|
|
|||
– график имеет две ветви, разде- |
|
|
|
|
|
||||||||||
ленные |
вертикальной |
асимптотой |
|
|
|
|
|
||||||||
x 1; ветви возле асимптоты стремят- |
|
|
|
|
|
||||||||||
ся к слева и справа; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
– при x ветвь графика стре- |
|
|
|
|
|
||||||||||
мится снизу к |
наклонной |
асимптоте |
|
|
|
|
|
||||||||
y x 2; |
при x ветвь |
графика Рис. 10.8. Эскиз графика |
|||||||||||||
стремится к той же асимптоте сверху; |
|
|
функции y |
x3 |
|||||||||||
|
|
2 |
|
||||||||||||
x 1
– нуль функции y 0 имеет место при x 0;
166

– в интервале , 0 функция отрицательна, а в интервалах
0,1 и 1, – положительна;
– известны координаты функции в пробных точках:
y 1 1, y 0,5 0,5, y 2 8. 4
2. Исследование с использованием производных.
2.1. Находим критические точки первого рода:
|
|
|
|
|
|
x3 |
|
|
|
x2 x 3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 |
... |
2 ; |
||||||
|
|
|
|
|
||||||||
|
|
|
|
x 1 |
|
|
|
x 1 |
||||
x2 x 3 |
0 x x |
|
0, x 3. |
|||||||||
x 1 2 |
|
2 |
||||||||||
|
|
1 |
3 |
|
||||||||
|
|
|
|
|
|
|||||||
Имеем две критические точки первого рода, являющиеся точками стационарности. Находим значения функции в этих точ-
ках: y 0 0, |
y 3 |
33 |
6,75; M1 0, 0 , M2 3; 6,75 . |
|
3 1 2 |
||||
|
|
|
2.2. Находим критические точки второго рода:
|
|
|
|
|
|
|
6x |
6x |
|||
|
|
|
x2 x 3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
y |
|
2 |
... |
4 ; |
4 0 x 0. |
||||||
|
|
|
|||||||||
|
|
|
|
x 1 |
|
|
x 1 |
x 1 |
|||
Получили одну критическую точку второго рода M1 0, 0 ,
которая совпадает с точкой стационарности.
2.3. Составим сводную таблицу результатов, необходимых для построения графика (табл. 10.4).
|
|
|
|
|
Таблица 10.4 |
||
|
Характеристика поведения функции y |
x3 |
|||||
|
2 |
|
|||||
|
|
|
|
|
x 1 |
||
|
Знак или |
Знак пер- |
Знак вто- |
|
|
|
|
Характерные |
числовое |
вой произ- |
рой произ- |
Краткая характеристика |
|||
точки (х) и |
значение |
водной |
водной |
поведения функции |
|||
интервалы |
функции |
функции |
функции |
||||
|
|
|
|||||
|
f(x) |
f (х) |
f (х) |
|
|
|
|
,0 |
– |
+ |
– |
Отрицательна, возрастает, |
|||
|
|
|
|
выпукла вверх |
|||
167
|
|
|
|
|
|
|
|
|
|
Окончание табл. 10.4 |
|||
|
Знак или |
|
|
Знак пер- |
Знак вто- |
|
|
|
|
||||
Характерные |
числовое |
|
вой произ- |
рой произ- |
Краткая характеристика |
||||||||
точки (х) и |
значение |
|
|
водной |
|
водной |
поведения функции |
|
|||||
интервалы |
функции |
|
|
функции |
функции |
|
|||||||
|
|
|
|
|
|
||||||||
|
|
f(x) |
|
|
f (х) |
|
|
f (х) |
|
|
|
|
|
х = 0 |
|
0 |
|
|
0 |
|
|
0 |
|
Нуль функции, критиче- |
|||
|
|
|
|
|
|
|
|
|
|
ская точка первого рода – |
|||
|
|
|
|
|
|
|
|
|
|
экстремума нет, критиче- |
|||
|
|
|
|
|
|
|
|
|
|
ская точка второго рода – |
|||
|
|
|
|
|
|
|
|
|
|
|
перегиб |
|
|
(0, 1) |
|
+ |
|
|
+ |
|
|
+ |
|
Положительна, возраста- |
|||
|
|
|
|
|
|
|
|
|
|
ет, выпукла вниз |
|
||
х = 1 |
|
|
|
|
|
|
|
|
|
Точка разрыва второго |
|||
|
|
|
|
|
|
|
|
|
|
|
рода |
|
|
(1, 3) |
|
+ |
|
|
– |
|
|
+ |
|
Положительна, убывает, |
|||
|
|
|
|
|
|
|
|
|
|
выпукла вниз |
|
||
х = 3 |
|
6,75 |
|
|
0 |
|
|
+ |
|
Критическая точка перво- |
|||
|
|
|
|
|
|
|
|
|
|
го рода – минимум |
|
||
3, |
|
+ |
|
|
+ |
|
|
+ |
|
Положительна, возраста- |
|||
|
|
|
|
|
|
|
|
|
|
ет, выпукла вниз |
|
||
2.4. Определяем характер монотонности и выпуклости функ- |
|||||||||||||
ции в интервалах, приведенных в сводной таблице. |
|
|
|
||||||||||
Интервал |
,0 : |
xпр 0,5; |
|
|
|
– |
|||||||
y |
0,5 0, |
y |
0,5 0 |
||||||||||
функция возрастает и выпукла вверх. |
|
|
|
|
|
||||||||
Интервал |
0,1 : |
xпр 0,5; |
|
|
|
|
|
|
– функция |
||||
|
y 0,5 0, |
y 0,5 0 |
|||||||||||
возрастает и выпукла вниз. |
|
|
|
|
|
|
|
|
|||||
Интервал 1, 3 : |
|
|
|
|
|
|
|
|
|
|
|||
xпр 2; y |
2 0, |
y 0,5 0 – функция убы- |
|||||||||||
вает и выпукла вниз. |
|
|
|
|
|
|
|
|
|
|
|
||
Интервал 3, : |
|
xпр 4; |
|
|
|
функция воз- |
|||||||
|
y |
4 0 |
, y |
4 0 – |
|||||||||
растает и выпукла вниз.
Заносим полученные результаты в сводную таблицу.
2.5. Определяем возможные экстремумы в критических точках первого рода.
Данные точки являются точками стационарности ( y 0), по-
этому можно использовать два достаточных условия экстремума. Согласно первому условию в окрестности точки M1 0, 0 первая
168

|
|
|
|
производная не меняет свой знак y 0,5 |
|||
му она не является точкой экстремума. |
|||
В |
окрестности |
точки |
M2 3; 6,75 |
первая производная меняет свой знак |
|||
|
|
плюса |
на минус, |
y 2 |
0, y 4 0 с |
||
значит, в данной точке – минимум. Проверим это, используя второе дос-
таточное |
условие |
экстремума: |
||
|
6 3 |
0 – минимум. |
||
3 1 2 |
||||
y 3 |
||||
2.6. Определяем, является ли критическая точка второго рода M1 0, 0 точ-
кой перегиба.
В окрестности точки x 0 вторая производная изменяет свой знак
y 0,5 0, y 0,5 0 , значит, М1(0, 0) –
точка перегиба.
2.7. По данным сводной таблицы и эскизу графика строим график функции
(рис. 10.9).
0, y 0,5 0 , поэто-
Рис. 10.9. График
функции у |
x3 |
|
x 1 2 |
||
|
Задачи к теме 10
10.1. Построить графики многочленов:
а) y x x3 ; б) y x x3 ; в) y x3 3x2 x 3.
36
10.2.Построить графики многочленов:
а) y 4x3 x4 6x2 4x 1; б)y 1 x2 x4 ; 2
в) y 1 x2 x4 .
224
10.3.Построить графики функций:
x2
а) y ex2 ; б) y e 2 ; в) y xe x ; г) y x2ex.
169
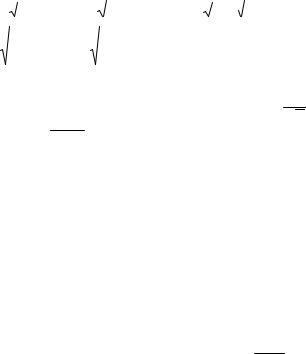
10.4. Построить графики функций:
а) y |
|
1 |
|
|
; б) |
y |
|
|
|
|
x |
|
; в) y |
|
x2 |
|
|
; г) y |
|
x3 |
|
. |
|||||||||||||||||||||
1 x2 |
|
|
|
|
|
|
1 x |
2 |
|
|
|
|
|
1 x |
2 |
|
|
|
|
|
|
|
1 x2 |
|
|||||||||||||||||||
10.5. Построить графики функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
а) y |
|
|
|
|
|
1 |
|
|
|
|
|
; б) y |
|
|
x 3 |
|
|
; в) y |
|
x2 2x 3 |
. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x x2 |
|
||||||||||||||||||||||||
1 x x2 |
|
|
|
|
|
|
|
1 x x2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
10.6. Построить графики функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
а) y |
|
x2 |
|
; б) y |
|
|
x2 |
; в) y |
|
|
x3 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
x2 1 |
x2 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
10.7. Построить графики функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
ex |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а) y 2x 2 ; б) y e x |
|
|
; в) y ex 2 ; г) |
|
y |
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
10.8. Построить графики функций: |
|
|
|
|
|
1 x |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
; б) y |
|
|
|
; в) y 3 |
|
3 |
|
; |
|
||||||||||||||||||||||||||||
а) y x |
|
|
|
|
|
|
4x x2 |
x2 1 |
|
||||||||||||||||||||||||||||||||||
1 x |
x |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
г) y 3 |
|
|
x |
2 |
|
|
; д) y |
|
|
|
|
x |
3 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x 1 |
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
10.9. Построить графики функций:
а) y ln x2 6x 8 ; б) y ln 8x x2 15 ; в) y lnx;

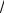 x
x
г) y ln x 
 1 x2 .
1 x2 .
10.10. Построить графики периодических функций:
а) |
y sinx sin2x; б) y cos2x cos3x; |
||||||||
в) |
y sinx |
1 |
sin2x |
1 |
sin3x; г) |
y tg x ctgx; |
|||
|
|
||||||||
|
2 |
|
4 |
|
1 |
|
|
||
д) |
y sin4 x cos4 |
x; е)y |
|
. |
|||||
|
|
||||||||
|
|
|
|
|
|
|
sinx cosx |
||
10.11.Построить графики периодических функций:
а) y ecosx; б) y lncosx.
10.12.Построить графики функций:
а) y x arctgx; б) y xarctg x; в) y arccos x 1. x 2
170
