
m0936
.pdf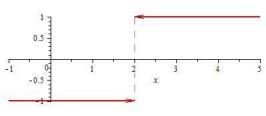
7.3.1. а) Единственная точка разрыва x 1 является точкой разрыва второго рода; б) единственная точка разрыва x 0 является устранимой точкой разрыва; в) бесконечное количество точек разрыва x n, n Z , все точки второго рода; г) единственная точка разрыва x 0 – устранимая.
7.3.2. а) Функция непрерывна на всей числовой прямой; б) единственная точка разрыва x 0 – разрыв первого рода; в) единственная точка разрыва x 0 – устранимая.
7.3.3. Покажем, что при различных способах стремления x 0 значения функции будут стремиться к разным пределам. Наличие как минимум
двух предельных точек будет означать отсутствие предела. |
|
|
|
|||||||||||||||||
|
|
Полагаем |
x |
|
1 |
|
, |
тогда |
lim |
|
1 |
|
0, |
а |
||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n |
2 n |
|
n |
2 n |
|
|
|
||||||
1 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sin |
|
|
sin |
|
2 n 1. Получили, что если предел существует, то он ра- |
|||||||||||||||
xn |
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||||
вен |
1. Пусть |
теперь |
x |
, тогда |
снова |
lim |
|
0, |
но |
|||||||||||
|
1 |
|
|
|
|
|
|
n |
2 n |
|
|
n 2 n |
|
|||||||
sin |
|
sin 2 n 0. Теперь получили, что если предел существует, то |
||||||||||||||||||
|
|
|||||||||||||||||||
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
он равен нулю. Функция не может иметь двух различных пределов в одной точке, значит, предел не существует.
7.4.1. Единственная точка разрыва – x 2, |
lim y 1, |
lim y 1. |
График – рис. 7.7. |
n 2 0 |
n 2 0 |
|
|
Рис. 7.7. Решение задачи 7.4.1 |
|
|
|
|
7.4.2. Единственная точка разрыва – x 2, lim |
y , |
lim y . |
||
График – рис. 7.8. |
n 2 0 |
|
|
n 2 0 |
|
|
|
|
|
7.4.3. Единственная точка разрыва – x 2, |
lim y 4, |
lim |
y 3. Гра- |
|
|
n 2 0 |
|
n 2 0 |
|
фик – рис. 7.9.
71

Рис. 7.8. Решение задачи 7.4.2 |
Рис. 7.9. Решение задачи 7.4.3 |
||||
7.4.4. а) |
|
и |
|
; б) 1 и 0; в) первый предел не существует, второй – |
|
2 |
2 |
|
|
||
равен 0.
7.4.5. а) Функция имеет разрывы первого рода во всех целочисленных точках; б) функция непрерывна на всей числовой прямой; в) функция име-
ет разрывы первого рода в точках x k, k Z ; г) функция непрерывна
2
на всей области своего существования в предельной точке x 0 – правый разрыв второго рода.
7.4.6. а) Устранимые разрывы в точках x 0 и x |
n |
|
1 |
, n Z ; б) раз- |
|
||||
|
|
n |
||
рыв второго рода в точке x 2; в) разрыв второго рода |
в точке x1 1 и |
|||
устранимые разрывы в точках x2 0 и x3 1; г) устранимый разрыв в точ-
ке x 0 и разрывы второго рода в точках xn n, n Z, n 0.
7.5.1. а) Разрыв второго рода в точке x = 2; б) разрыв второго рода в точке x 1; в) разрыв второго рода в точке x 0. Эскизы представлены на рис. 7.10.
а) б) в)
Рис. 7.10. Решение задачи 7.5.1
72

7.5.2.Разложить сложную функцию на «внешнюю» f, «среднюю» и «внутреннюю» , определить точки разрыва «внешней», «средней» и «внутренней» функций, исследовать поведение сложной функции в окрестностях всех этих точек.
7.5.3.а) В точках xn e n,n Z – разрывы второго рода, в предельной
точке области существования x 0 – правый разрыв второго рода; б) раз-
рывы второго рода в точках x n, n Z |
и точках x |
|
|
n, n Z ; |
|
||||
n |
n |
2 |
|
|
в) разрывы второго рода в точках xn n, n Z ; г) разрывы второго рода в
точках xn 2n2, n Z; д) разрывы второго рода в точках n Z ; е) разрывы второго рода в точках xn e 2 n, n Z .
7.5.4. Функция f x исследуется с помощью рассмотренного в раз-
деле 7.5 алгоритма, затем отбрасываются точки разрыва, не удовлетво-
ряющие условию x x0 ; затем так же исследуется функция |
g x и от- |
брасываются точки разрыва, не удовлетворяющие условию |
x x0 . На за- |
вершающем этапе вычисляются пределы lim f x и lim |
g x и де- |
лается вывод о наличии или отсутствии разрыва в точке x0 .
7.5.5. а) В точках xn 
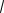 n, n N 0 – разрывы второго рода, в точке x 1 – разрыв первого рода; б) x 0 – устранимая точка разрыва, xn n, n Z, n 0– разрывы второго рода.
n, n N 0 – разрывы второго рода, в точке x 1 – разрыв первого рода; б) x 0 – устранимая точка разрыва, xn n, n Z, n 0– разрывы второго рода.
Требования к практическому усвоению темы «Непрерывные и разрывные функции одной действительной переменной»
Студент должен знать:
–три определения непрерывности функции в точке, распространение этих определений на промежуток и область существования (определения) функции;
–определение односторонних пределов и представление графиков функций в окрестности точек разрыва;
–способы вычисления односторонних пределов в случаях разрывов первого и второго рода, а также устранимых разрывов;
–методику исследования непрерывности сложной функции с определением поведения функции в окрестности точек разрыва.
Студент должен уметь:
73
–определять интервалы непрерывности функции с выделением точек разрыва;
–исследовать с помощью односторонних пределов поведение функции, в том числе сложной функции, в окрестности точек разрыва, отражать в графической форме особенности поведения функции в окрестности указанных точек (стремление к или конечным пределам, односторонняя непрерывность в точке).
74
Тема 8: Производная и дифференциал функции одной действительной переменной. Алгоритмы дифференцирования
8.1.Исходные положения
Воснове операции дифференцирования функции лежат понятия предельного перехода и непрерывности функции.
Производной функции y f x называется предел отношения
приращения функции y |
к приращению аргумента x при про- |
|||||
извольном стремлении приращения x к нулю: |
||||||
lim |
f x0 x f x0 |
lim |
y |
|
dy x0 |
f x0 y x0 . |
x |
|
|
||||
x 0 |
x 0 x |
|
dx |
|||
Замечание 1. f (x0), y (x0) – условные обозначения производной, выра-
жение dy x0 пока будем воспринимать как единый знак и также считать dx
условным обозначением производной.
Замечание 2. Поскольку предел функции необязательно существует, а производная определена как предел, то производная существует не для любой функции и не в любой точке.
Производная функции в фиксированной точке, если она существует, может принимать следующие значения:
A конечное ненулевое число, f x0 0,
.
Геометрический смысл производной функции в точке M0 x0,y0 заключается в следующем: производная функции в точке M0 x0,y0 равна тангенсу угла между ка-
сательной к графику функции в точке M0
и положительным направлением оси Ox Рис. 8.1. Касательная и
(рис. 8.1). |
нормаль |
|
|
В символьной форме геометрический смысл производной |
|
можно представить так: tg 0 |
y M0 . |
75
Перпендикуляр к касательной, проведенный в точке касания М, называется нормалью к линии L в точке M.
Уравнение касательной к линии y y x в точке M0 x0, y0 : y y0 y x0 x x0 ;
уравнение нормали:
1
y y0 y x0 x x0 .
Производная в фиксированной точке x x0 , если она сущест-
вует, является конечным числом (в частности, нулем) или равна бесконечности. При этом из геометрического смысла производ-
ной следует, |
что при |
|
|
|
|
|
|
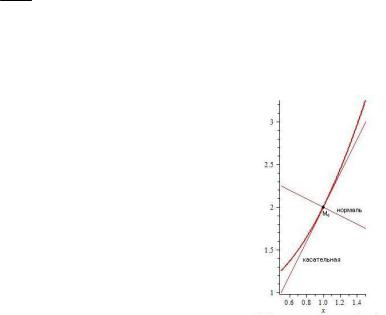
y A 0 касательная в точке A графика |
|||||||
кривой параллельна оси |
Ox tg 0 0 . При |
|
ка- |
||||
y B |
|||||||
|
точке B |
|
|
|
|
|
|
сательная в |
|
параллельна оси |
Oy tg |
|
, |
||
|
|
||||||
|
|
|
|
|
|
2 |
|
рис. 8.2.
Рис. 8.2. Касательные, соответствующие нулевой и бесконечной производным
Функции, имеющие производные во всех точках интервала непрерывности, будем называть гладкими.
Гладкие функции могут иметь нулевые и бесконечные значения производной. График гладкой функции будем называть гладкой кривой. В каждой точке гладкой кривой можно построить касательную.
76

Если в некоторой точке x x0 интервала непрерывности
a,b непрерывная функция y y x не имеет производной, то ее называют негладкой.
Точки, в которых производная непрерывной функции не существует, называются особыми. В этих точках график непрерывной функции не имеет касательной, но в окрестности особых точек функция может иметь односторонние касательные и соответствующие им односторонние производные.
Замечание 1. Далее в материалах темы 8 будем рассматривать непрерывные функции без особых точек. Функции, имеющие особые точки, и приложения таких функций будут рассмотрены в материалах темы 9.
Замечание 2. Процесс нахождения производных называется дифференцированием функций. Смысл этого термина будет разъяснен чуть позднее.
Задачи к разделу 8.1
8.1.1. а) Показать, что если функция имеет производную в точке x0 , то она непрерывна в этой точке; б) показать, что суще-
ствуют непрерывные функции, не имеющие производной. Рас-
2
смотреть функции y x и y x3 в точке x0 0.
8.1.2. а) На примере графика функции y x2 и прямой x 0
показать, что нельзя определять касательную как прямую, имеющую с графиком функции единственную общую точку; б) пользуясь определением касательной как предельного положения секущих, доказать, что касательной к прямой является сама эта прямая.
8.1.3. а) Убедиться, что касательная к графику функции
|
|
|
|
|
|
|
|
y 3 x в точке x 0 существует, |
хотя и не может быть найдена |
||||||
0 |
|
|
|
|
|||
по формуле y y0 y x0 x x0 ; |
б) убедиться, что нормаль к |
||||||
графику функции y x3 в точке x |
0 существует, хотя и не мо- |
||||||
0 |
|
|
|
|
|||
жет быть найдена по формуле y y0 |
1 |
|
x x0 . |
||||
y x0 |
|||||||
|
|
|
|
|
|||
8.1.4. Пользуясь определениями производной и односторонних пределов, дать определения левой и правой производных и левой и правой касательных.
77

8.2. Основной алгоритм нахождения производных элементарных функций
|
Из определения производной lim |
|
f x0 x f x0 |
f x0 |
||||||
|
|
|
||||||||
|
|
|
|
|
|
x 0 |
x |
|
|
|
получаем следующий алгоритм ее нахождения: |
|
|
||||||||
1. |
Придаем аргументу x известной функции y f x |
прираще- |
||||||||
|
ние x и находим значение функции для аргумента с прира- |
|||||||||
|
щением x x; при x 0 y y f x x f x . |
|
|
|||||||
2. |
Определяем приращение функции: y f x x f x . |
|||||||||
3. |
Находим |
среднее относительное |
приращение |
функции: |
||||||
|
|
y |
|
f x x f x |
. |
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
x |
x |
|
|
|
||||
4.Вычисляем предельное значение относительного приращения функции, которое является производной данной функции:
lim f x0 x f x0 f x0 .
x 0 x
Пример 1. Найти производную функции y 
 x в точке x0 4 на основе определения.
x в точке x0 4 на основе определения.
Решение:
1)y y 
 x x;
x x;
2)y 
 x x
x x 
 x ;
x ;
3)y 
 x x
x x 
 x ;
x ;
x x
4) lim |
y |
lim |
|
x x |
x |
|
|
|
x x |
x |
|
|
|
|
|
|
||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x 0 x |
|
x 0 |
|
|
|
|
|
|
|
|
|
x x x |
|
|
|
|
|
|
||||||||||||||
lim |
|
x x x |
lim |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x 0 x |
|
x x x |
x 0 |
|
|
x x x 2 |
|
x |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||
при x0 4 получим y 4 |
2 |
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
2x |
|
||||||
Пример 2. Найти производную функции |
y |
|
на ос- |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 1 |
|
нове определения.
78
Решение:
1) |
|
y y |
2 x x |
|
; |
|
|
|
|
|
|
|
|
|
|||||||
|
3 x x 1 |
|
|
|
|
|
|
|
|
|
|||||||||||
2) y |
|
|
|
2 x x |
|
2x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 x x 1 |
3x 1 |
|
|
|
|
|
|
||||||||||||||
|
2 x x 3x 1 2x 3 x x 1 |
|
|
2 x |
; |
||||||||||||||||
|
|
|
|
|
3 x x 1 3x 1 |
|
3x 3 x 1 3x 1 |
||||||||||||||
3) |
|
y |
|
|
|
2 |
|
|
|
|
; |
|
|
|
|
|
|
||||
|
x |
3x 3 x 1 3x 1 |
|
|
|
|
|
|
|||||||||||||
4) |
|
lim |
y |
lim |
|
2 |
|
|
|
|
|
2 |
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
3x 1 2 |
|
||||||||||
|
x 0 x |
x 0 3x 3 x 1 3x 1 |
|
|
|
||||||||||||||||
Задачи к разделу 8.2
8.2.1. а) Пользуясь определением, найти производную постоянной функции y C; б) что можно сказать о производной ку-
сочно-постоянной функции?
8.2.2.Пользуясь определением, найти производные тригонометрических функций:
а) y sinx; б) y cosx; в) y = tg x; г) y = ctg x.
8.2.3.Пользуясь определением, найти производные функций:
а) y x ; б) y ax; в) y ex ; г) y loga x; д) y lnx.
8.2.4.Пользуясь результатами предыдущей задачи, найти
производные функций:
а) y x100; б) |
y |
1 |
; в) |
y 3 |
|
; г) |
y |
1 |
|
; д) y x |
|
; |
||
x |
x |
|||||||||||||
x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
||||||
е) y 5x; ж) y 2 x .
8.3. Табличные производные. Правила дифференцирования
Вычисление производных можно существенно упростить, если вместо основного алгоритма дифференцирования (см. раздел 8.2) использовать готовые формулы для производных основных элементарных функций и правила дифференцирования.
79

Производные всех основных элементарных функций сводятся в таблицу (табл. 8.1) и называются табличными производными,
а эти функции – табличными функциями.
Таблица 8.1
Таблица производных основных элементарных функций
Наименование функции |
Функция y f x |
Производная y |
|
f |
|
|||||||||||||||||||||||
|
x |
|||||||||||||||||||||||||||
Постоянная |
y const |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||
Степенные функции |
y x , R |
|
|
|
x 1 |
|
|
|
||||||||||||||||||||
|
y x x1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
y |
|
x |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
x |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
y |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
x |
|
|
|
|
x2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Показательные функции |
y ax |
|
|
ax lna |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y ex |
|
|
|
|
|
|
|
|
ex |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Логарифмические функ- |
y loga x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
ции |
|
|
|
|
xlna |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y lnx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Тригонометрические |
y sinx |
|
|
|
cosx |
|
|
|
||||||||||||||||||||
функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y cosx |
|
sin x |
|
|
|
|||||||||||||||||||||||
|
y tgx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
cos2 x |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y ctgx |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
sin2 x |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Обратные тригонометри- |
y arcsinx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
ческие функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 x2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y arccosx |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 x2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y arctgx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 x2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y arcctgx |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
||||||||||
Замечание. Формулы для производных не изменяются по форме при использовании любых других аргументов u, t и т.п., если и функции с новыми аргументами остаются основными элементарными.
80
