Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

m0936

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

7.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2912 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

8.4.2. y

3 x ln3

1 9

x .

8.4.3. а)

y 2lnsin x ln2ctgx; б) y

2sinlnx ln2cosln x

;

в)

2lnx ln2cos2ln x

; г)

y cosln2x ln2; д)

y 2x ln2ctg2x ;

е)

y cosx ln2.

8.4.4. а)

y cos sin sin x cos sin x cosx;

б) y

2 x

;

2 x

x2 x 1 xlnx

x 2x 2

ln21 2

x 2

ln2 .

в)

x x ln x ln x x lnx ; г) y

8.4.5. а)

y arctg x; б) y arcsin x; в) y

; г)

;

x2 a2

д) y a2 x2 .

8.4.6. а)

; б)

; в)

1 x3

x4 1

1 x6

8.5.1. а)

3x 5 10 x2 6x 18

10 2x 3

8 2x 6

x2 5x 2 12 x2 4x 3 9

3x 5

x2 6x 1

12 2x 5

9 2x 4

;

x2 5x 2

x2 4x 3

2x 3

3x 4

б) y

;

6x 9

12x 16

20x 25

4x 5 5x 6

10x 12

arctg

в) y

x e

x x 1

2x 1

2 x

x 1

3 x

3 x3 x2 x 1

1 x

x 1

8.5.2. а)

ln x 1 ; б)

y x

ln x

;

1 x

в) y 1

ln 1

;

x 1

4x 5

г) y x

3x 4

2x 4 ln x

4 2x 3

;

3x 4

д) y xxx xx ln x 1 ln x xx 1 .

111

8.6.1. а)

1 ; в)

x ; б)

x3 1 3

;

x3 1 2

г) y

cos2 x.

8.6.2. а)

y 10

0; б)

y10

ex ; в) y 10 2x ln10 2; г)

y 10 cosx;

д) y 10

1 024

sin

2 x ; е)

y10

362880

; ж)

y 10

362880

x10

x10 lna

8.6.3. а)

; б)

a; в) y

sin x

;

n 1

г) y

cos x

; д)

1 !x

;

е) y n

1 n 1 n 1 !x n

; ж) y n 1 n 1 x n .

8.7.1. а)

lna

1 (кроме некоторых точек,

в которых она не существу-

ет); б) yx

sint

b et

e t

; д) yx

ctgt; в)

; г)

1 cost

e t

12cost

8.7.2.а) yx yx 0; б) yx sin2 t , yx sin2 t ;

в) yx	cost cos2t	, yx	sint 5cost 4cos2 t 2sin	2 t
					.
	1 cost 2		1 cost 3

8.7.3. а) а – одну (рис. 8.9); б – две (рис. 8.10); в – одну (рис. 8.11); г – две и двумя способами (рис. 8.12); д – две (рис. 8.13); б) а – производная не

существует в точках t n, n Z ; б – производная бесконечна в точках

t n, n Z ; в – производная не существует в точках t 2 n, n Z ; г – производная бесконечна в точке t 0; д – производная не существует в точках t 2 n, n Z .

Рис. 8.9. Решение задачи 8.7.3, а	Рис. 8.10. Решение задачи 8.7.3, б
	при а = 2, b = 3 и при а = 3, b = 1

112

Рис. 8.11. Решение задачи 8.7.3, в	Рис. 8.12. Решение задачи 8.7.3, г
при а = 1 и а = 2	при а = b = 1 и при а = 2, b = 6

Рис. 8.13. Решение задачи 8.7.3, д при R = 1, R = 2

8.8.1. Уравнение x2 y2 1 0, переписанное в виде x2 y2 1, не

имеет решений, так как его левая часть неотрицательна, а правая – отрицательна.

8.8.2. а) Уравнение не задает линии; б) две; в) две и двумя различными способами; г) две и двумя различными способами; д) бесконечно много.

8.8.3. а)

y x2

; в) y

; б) yx

x 1 2x

8.8.4. а)

y x

1 1; б)

x2 y2

113

5 3

8.8.5. а)

; б) yx

x2 3 x4

8.9.1. а)

lna; б)

; в) ; г)

; д) 0; е) 0; ж) 0.

lna

8.9.2. а) 2; б) 16; в) 1; г) 1 ; д) 1. 2 2 3

8.9.3.а) 0; б) 0; в) ; г) .

8.9.4.а) 1; б) e; в) 1; г) 1; д) 1.

8.10.1. а)						e																и x 0;
8.10.1. а)	y x 1			и y 1 x; б)			y x 3 и y x 3; в) y 0															и x 0;
г) x 1 и y 0.
							x		7				; б)
8.10.2. а)	y		x 4			и y						3			y 3 и x 0.
		3			3							3
											6
							3
							3
8.10.3. а)	y x 2			и y x; б) y				2		x 2					и y	3	x	7		2	;
8.10.3. а)	y x 2			и y x; б) y				2		x 2				2	и y	3	x	7		2	;
							3								2				2

в) y x 2 и y x.

8.10.4.а) Можно сначала перейти к прямоугольной системе коорди-

arctg

, то x0

нат:

x2 y2

. Поскольку 0

откуда полу-

y0 x0

y x

x2 y2

чаем

2 .

Производная

равна:

x y

x2 y2

откуда

. Уравнение

касательной

уравнение

4 2 4

4 2

нормали

1 2x

x2 y2 x

б)

Находим

аналогично.

Получим

x2 y2

x0 0, y0

1. Уравнение касательной

y x 1,

уравнение нормали

1, y0

yx 1.

8.10.5.а) Левая касательная y x, левая нормаль y x , правая касательная y x , правая нормаль y x; б) левая и правая каса-

114

тельные y 0 совпадают, соответственно совпадают левая и правая нор-

мали x 1.

8.10.6. a 2, b 3. 8.10.7. a2 1, b2 2. 8.10.8. а) arctg 3; б) 90 .

		3		4
8.10.9. а) В точке x 1 угол равен	arctg	3	, в точке	x 0 кривые пер-
8.10.9. а) В точке x 1 угол равен	arctg		, в точке	x 0 кривые пер-
1	4			0
	4

пендикулярны; б) в обеих точках пересечения кривые перпендикулярны; в) в обеих точках пересечения кривые перпендикулярны.

8.10.10. а) В обеих точках пересечения линии перпендикулярны; б) во всех четырех точках пересечения кривые перпендикулярны.

2 UdR

8.12.2. а) ds gtdt ; б) dV 4 R dR; в) dI R2 .

8.12.3. а) 2,083; б) 0,8104; в) 1,043; г) 0,4849. 8.12.4. 0,0037 м.

8.12.5.1 %. 8.12.6. 565 см3. 8.12.7. 1004 Дж. 3

Требования к практическому усвоению темы «Производная и дифференциал функции одной действительной переменной.

Алгоритмы дифференцирования»

Студент должен знать:

–определение производной, ее геометрический смысл, основной алгоритм нахождения производных явно заданных функций;

–таблицу производных основных элементарных функций и правила дифференцирования составных элементарных функций, составленных из основных элементарных функций с помощью четырех арифметических действий;

–способы нахождения производных сложных функций;

–способ логарифмического дифференцирования функций, в том числе показательно-степенных функций;

–способ нахождения производных второго и более высоких порядков;

–способы нахождения производных неявных и параметрически заданных функций;

–условия, при которых можно использовать правило Бернулли – Лопиталя при вычислении пределов элементарных функ-

115

ций с различными видами неопределенностей, а также общий алгоритм вычисления пределов с помощью указанного правила;

–геометрический и прикладной смысл производных;

–уравнения касательной и нормали к кривой и способ их определения по заданному уравнению кривой;

–способ вычисления угла пересечения кривых;

–способ вычисления дифференциала функции и его применение в приближенных вычислениях.

Студент должен уметь:

–находить производные составных элементарных функций с помощью табличных производных и правил дифференцирования;

–находить производные сложных функций любым из двух способов (с целью использовать один способ для вычисления, другой – для проверки);

–использовать логарифмическое дифференцирование для нахождения производных функций;

–находить производные любого порядка явных, неявных и параметрических заданных функций;

–вычислять пределы функций с различными видами неопределенностей с помощью правила Бернулли – Лопиталя;

–определять уравнения касательной и нормали в заданной точке по известному уравнению кривой;

–строить касательные и нормали по известным уравнениям кривых;

–находить координаты точек пересечения кривых и угол их пересечения в этих точках;

–использовать дифференциал функций в приближенных вычислениях и для приближенной оценки влияния изменения одной величины на другую, если они связаны между собой известной функциональной зависимостью.

116

Тема 9: Основные свойства функций

9.1. Исходные положения

При решении инженерных задач проводят исследования функций с целью выявления особенностей поведения (свойств) функций в области естественного существования или в промежутках, входящих в указанную область.

Под поведением функции понимают закономерности изменения числовых значений функции в заданном интервале значений аргумента.

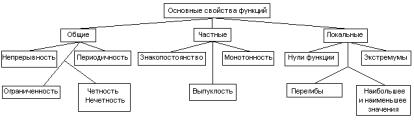
Основные свойства функций можно разделить на общие, частные и локальные (рис. 9.1).

Рис. 9.1. Основные свойства функций

Общие свойства – это свойства, характеризующие поведение функции в целом в области ее существования. Наиболее существенным общим свойством функции является ее непрерывность.

Кроме общих свойств, характеризующих поведение функции в целом, для прикладных задач важны частные свойства функций, которыми они обладают в отдельных частичных интервалах, входящих в интервал непрерывности функции. Различные интервалы, входящие в область существования функции, выделяются характерными точками, которые ограничивают указанные интервалы снизу и сверху.

Важнейшими характерными точками функции являются:

–точки разрыва;

–нули функции;

–критические точки первого рода;

–критические точки второго рода.

117

Замечание. В точках разрыва функция может не существовать, но их относят к несобственным точкам области существования функции, так как они ограничивают интервалы непрерывности и частичные интервалы существования функции с различными частными свойствами.

Кроме частных свойств выделяют локальные свойства, которые характеризуют особенности поведения функций в отдельных точках и их окрестностях.

9.2.Общие свойства функций

Кобщим свойствам функций относятся их непрерывность, четность-нечетность, периодичность и ограниченность.

Непрерывность функции и ее точечные разрывы подробно рассмотрены в теме 7.

9.2.1.Четность и нечетность функции

Функция y f x называется четной, если она определена

на симметричном относительно нуля числовом множестве и удовлетворяет условию: для любого x из этого множества выполняется условие f x f x . Функция y f x называется

нечетной, если она определена на симметричном относительно нуля числовом множестве и удовлетворяет условию: для любого x из этого множества выполняется условие f x f x .

Примеры четных (y = x2, y = cos x) и нечетных (y = x3, y = tg x) основных элементарных функций приведены в прил. А. Графики четных функций симметричны относительно оси ординат, а графики нечетных – относительно начала координат (рис. 9.2, 9.3).

Произведение и частное двух четных или двух нечетных функций образуют четную функцию; произведение и частное четной и нечетной функции образуют нечетную функцию.

Большинство элементарных функций являются функциями общего вида, т.е. они не являются ни четными, ни нечетными.

118

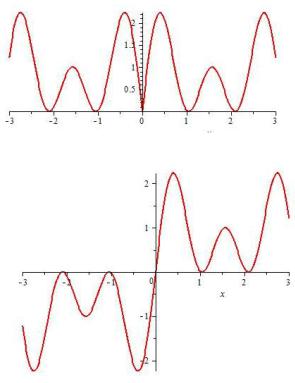
Рис. 9.2. График четной функции

Рис. 9.3. График нечетной функции

9.2.2. Периодичность функции

Функция y f x называется периодической, если существу-

ет такое положительное число T 0 (период), что от прибавления (вычитания) его к любому значению аргумента из области существования функции ее числовое значение не изменится:

f x T f x T f x .

Любая периодическая функция имеет бесконечное множество периодов:

f x T f x 2T ... f x nT f x , n N .

Сумма двух функций с одним и тем же периодом является периодической функцией с тем же периодом.

119

9.2.3. Ограниченность функции

Функция y f x называется ограниченной, если существует число M 0 такое, что абсолютное значение функции не превышает этого числа ( f x M ) для всех значений аргумента x из области существования (определения) функции.

При необходимости различают функции, ограниченные свер-

ху f (x) M ,	и функции, ограниченные снизу f (x) M .
Число M	называют точной	верхней гранью функции
y f x , если	f x M , но ни для	какого числа M1 M не вы-

полняется неравенство f x M1 хотя бы для одного значения аргумента x.

Число M	называют точной	нижней гранью функции
y f x , если	f x M , но ни для	какого числа M1 M не вы-

полняется неравенство f x M1 хотя бы для одного значения аргумента x.

Пример. Тригонометрические функции sinx и cosx имеют точную верхнюю грань M 1 и точную нижнюю грань m 1. При этом функция sinx достигает своей точной верхней

грани в точках			xk		2 k, а точной нижней грани – в точках

				2
xn		2 n.	Функция cosx также достигает своих точных

	2

верхней и нижней граней.

Обратная тригонометрическая функция arctgx имеет точную

верхнюю грань M и точную нижнюю грань m , однако

эта функция не достигает ни точной верхней грани, ни точной нижней грани. Указанная функция асимптотически приближается

к значениям . 2

Функции могут быть ограниченными с одной стороны (снизу или сверху) и не ограниченными с другой.

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2912 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022619.79 Кб0m0925 (1).pdf
#
15.11.2022619.79 Кб1m0925.pdf
#
15.11.20221.64 Mб4m0927.pdf
#
15.11.20222.37 Mб0m0931.pdf
#
15.11.20224.8 Mб2m0935.pdf
#
15.11.20227.46 Mб2m0936.pdf
#
15.11.20222.25 Mб0m0937.pdf
#
15.11.20221.7 Mб0m0938.pdf
#
15.11.20229.08 Mб1m0939.pdf
#
15.11.20223.68 Mб4m0940.pdf
#
15.11.20221.36 Mб0m0942.pdf